G锥度量空间中广义c距离的不动点定理

曹小双 ,林存津,刘 炜

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

G锥度量空间中广义c距离的不动点定理

曹小双 ,林存津,刘 炜

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

推广了Cho Yeol Je, Saadati Reza和Wang Shenghua的结果, 引入了广义c距离的概念, 并将广义c距离运用到G锥度量空间中来解决相关不动点问题. 去掉了算子的连续性, 锥的正规性等一系列附加条件, 与以往传统方法相比, 更具技巧性.

广义c距离;G锥度量空间; 不动点问题

0 引言

在过去二十年里，很多学者都致力于在抽象空间中研究压缩映射、或者广义压缩映射的相关不动点理论. 而最近几年里, 为了克服 Dhage理论中存在的问题, Mustafa Z和Sims B在文[1]中对度量空间作了一个更为合理的推广, 也就是所谓的G度量空间. 2010年, Beg I, Abbas M和Nazir T在文[2]中提出了G锥度量空间作为G度量空间的进一步推广. 为此, 一些作者在这类空间中研究了诸多的不动点理论, 见文[3,4,5].

我们知道, Cho Yeol Je等于2011年在锥度量空间中提出了c距离的概念, 并通过采用这一概念,在锥度量空间中证明了一系列的不动点理论. 不仅如此, 很多作者也运用这一工具在抽象空间中证明了相关不动点理论, 见文[6～10].

本文主要在此基础上对该c距离作了推广, 引入了广义c距离的概念, 并将其运用到近来才出现的G锥度量空间中来解决相关不动点问题, 该证明过程相比以往的常规方法, 具有很强的突破性.

1 预备知识

下面出现的定义、引理或者定理可能会在主要结果的获得过程中被用到.

让E是一个实巴拿赫空间,E的子集P被称作一个锥, 当且仅当以下条件成立:

a)P是非空闭集，而且P≠{θ} ;

b)a,b∈R,a,b≥0,x,y∈P⟹ax+by∈P;

c)P∩(-P)={θ} .

锥P被称作正规的, 如果存在一个实数K>0 使得对于所有的x,y∈E, 都有y≥x≥θ可以推出K‖y‖≥‖x‖ , 满足上述不等式的最小正数被称为P的正规常量. 这里x≤y当且仅当y-x∈P,x≪y当且仅当y-x∈intP(其中， intP指的是P的内部).

定义1[2]设X是一个非空集，假定映射G:X×X×X→E满足：

G1)对 ∀x,y,z∈X, 如果x=y=z, 则G(x,y,z)=0;

G2)对 ∀x,y∈X, 当x≠y时, 有G(x,x,y)>0;

G3)对 ∀x,y,z∈X, 当y≠z时,G(x,x,y)≤G(x,y,z) ;

G4)对∀x,y,z∈X, 有G(x,y,z)=G(x,z,y)=…(关于这三个元素满足对称关系);

G5)对∀x,y,z,a∈X，有G(x,y,z)≤G(x,a,a)+G(a,y,z) .

则G被称作X上的一个广义锥度量, 而且X被称作广义锥度量空间, 或者是G-锥度量空间.

注1 很显然, 我们可以得到, 对∀x,y,z∈X,G(x,y,z)=0当且仅当x=y=z.

引理1[2]对∀x,y∈X, 有G(x,y,y)≤2G(x,x,y) .

定义2[1]设X是一个G-锥度量空间,{xn}⊂X, 我们说{xn} 是:

a) 柯西列, 如果对∀c∈E, 而且c≫θ, 存在N, 使得对于∀m,n,l>N, 有G(xm,xn,xl)≪c;

b) 收敛列, 如果对∀c∈E, 而且c≫θ, 存在N, 使得对于 ∀m,n>N, 有G(xm,xn,x) ≪c，其中x为X中的一个不动点.

一个G-锥度量空间被称为完备的, 如果X中每一个柯西列在X中都是收敛的.

引理2[2]设X是一个G-锥度量空间,P是正规锥, {xn},{yn}和{zn} 是X中的三个序列, 如果xn→x,yn→y和zn→z, 则有G(xm,xn,xl)→G(x,y,z)(m,n,l→∞) .

引理3[2]设X是一个G-锥度量空间,P是正规锥, 若存在序列 {xn}⊂X, 点x∈X, 则下面的陈述是等价的:

i) {xn}收敛于x;

ii) G(xn,xn,x)→0(n→∞);

iii) G(xn,x,x,)→0(n→∞);

iv)G(xm,xn,x)→0(n→∞) .

定义3[9]设(X,d) 是一个锥度量空间, 则一个函数q:X×X→E被称为X上的一个c距离, 如果下面的条件满足:

q1)对∀x,y∈X, 有q(x,y)≥θ;

q2)对∀x,y,z∈X, 有q(x,z)≤q(x,y)+q(y,z) ;

q3)让yn→y∈X，对∀x∈X, 而且n≥1, 若存在u=ux∈P使得q(x,yn)≤u, 则有q(x,y)≤u;

q4)对于所有的x,y,z∈X,c∈E, 而且c≫θ, 存在e∈E, 而且e≫θ, 当q(z,x)≪e和q(z,y)≪e时, 我们可以得到d(x,y)≪c.

定义4[9]设一对映射(f,g) 是偏序集上的自映射对, 则(f,g) 被称为是弱增的, 如果对∀x∈X,fx≤gfx而且gx≤fgx.

2 主要结果

在得出本文的主要结果之前, 我们先给出如下新的定义.

定义5 设 (X,G)是一个G锥度量空间, 则函数Q:X×X×X→E被称作X上的一个广义c距离, 如果以下条件满足:

1 )对于所有的x,y,z∈X, 有Q(x,y,z) ≥θ;

2)对于所有的x,y,z∈X, 有Q(x,y,z)≤Q(x,a,a)+Q(a,y,z) ;

3) 让yn→y∈X, 对任意x∈X和n≥1, 如果存在一个u=ux∈P，使得Q(x,yn,y)≤u或者是

Q(x,y,yn)≤u, 则有Q(x,y,y)≤u;

4)对于所有的x，y,z∈X,c∈E,并且c≫θ, 存在一个e∈E, 并且e≫θ，当Q(z,x,x)≪e和Q(z,y,y)≪e时, 我们可以得到G(x,y,y)≪c或者是G(y,x,x)≪c.

引理4 设(X,G) 是一个G锥度量空间,Q是X上的一个广义c距离. 若存在序列{xn}⊂X, {un}⊂P, 并且un→θ, 假定对于所有的m>n, 存在一个N, 当n≥N时, 都有Q(xn,xm,xm)≤un, 则{xn} 是X中的一个柯西列.

引理5 设(X,G) 是一个G锥度量空间,Q是X上的一个广义c距离. 如果对于任意x,y,z∈X,都有Q(x,y,y)=θ和Q(y,x,x)=θ, 则我们可以得到x=y.

证明 因为

Q(x,y,y)=Q(y,x,x)=θ

则由条件2 ), 我们有θ≤Q(y,y,y)≤Q(y,x,x)+Q(x,y,y)=θ

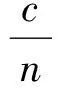
定理1 设(X,≤) 是一个偏序集, (X,G) 是一个完备的G锥度量空间,Q是X上的一个广义c距离, 假定存在映像f:X→X关于 ≤满足不减性, 且如下条件满足:

i)存在a,b>0 并且a+b<1 , 使得

Q(fx,fy,fz)≤aQ(x,y,z)+bQ(x,fx,fx)

对于所有的x,y,z∈X并且x≤y≤z;

ii)存在x0∈X使得x0≤fx0.

则f有一个唯一不动点，如果v=fv,则Q(v,v,v)=θ.

证明 如果fx0=x0, 则x0即为f的不动点, 证明完成. 现假设fx0≠x0, 因为x0≤fx0, 且映像f关于≤ 满足不减性, 则令xn=fnx0, 我们不难得到

x0≤fx0=x1≤f2x0=x2≤…≤fnx0=xn≤fn+1x0=xn+1≤…

又由条件(I), 显然有

Q(xn,xn+1,xn+1)=Q(fxn-1,fxn,fxn)≤aQ(xn-1,xn,xn)+bQ(xn-1,fxn-1,fxn-1)= (a+b)Q(xn-1,xn,xn)

于是, 对于所有的n≥1, 我们有Q(xn,xn+1,xn+1)≤hQ(xn-1,xn,xn)≤…≤hnQ(x0,x1,x1)其中h=a+b<1 . 现在证当m>n时, 由条件2 ), 我们有

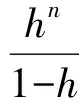
下面我们将证明 {xn}是柯西列.

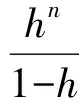
同理, 我们可以找到正数N1, 当n≥N1时,Q(xn-1,x′,x′)≪c,又因为

Q(xn,fx′,fx′)=Q(fxn-1,fx′,fx′)≤aQ(xn-1,x′,x′)+bQ(xn-1,fxn-1,fxn-1)=aQ(xn-1,x′,x′)+bQ(xn-1,xn,xn)

则类似可以找到正数N2, 当n≥N2时,Q(xn,fx′,fx′)≪c, 取e=c, 结合前面的Q(xn,x′,x′)≪C,由4) , 我们有G(fx′,x′,x′)≪c或者G(x′,fx′,fx′)≪c. 这说明了fx′=x′, 即x′ 为f的不动点.

假定v=fv, 则有

Q(v,v,v)=Q(fv,fv,fv)≤aQ(v,v,v)+bQ(v,fv,fv)=(a+b)Q(v,v,v)

因a+b< 1, 故Q(v,v,v)=θ显然成立.

下证唯一性.

若存在另一不动点y′ , 使得fy′=y′, 则有

Q(fx′,fy′,fy′)≤aQ(x′,y′,y′)+bQ(x′,fx′,fx′)≤aQ(x′,y′,y′)

和

Q(fy′,fx′,fx′)≤Q(y′,x′,x′)+bQ(y′,fy′,fy′)≤aQ(y′,x′,x′)

因a<1 , 故Q(x′,y′,y′)=θ且Q(y′,x′,x′)=θ, 由引理5, 我们有

x′=y′

唯一性得证, 证毕.

注2 在定理1的证明过程中, 我们去掉了文[9]定理3.1中f的连续性这一条件, 取而代之,我们用3) 和4) 来得出我们想要的结果, 此方法很好地实现了把广义c距离作为解题工具的实效性.

定理2 设(X,≤) 是一个偏序集,(X,G) 是一个完备的G锥度量空间,Q是X上的一个广义c距离, 假定存在两个映像f,g关于≤ 满足弱增性, 且存在a,b>0并且a+b<1, 使得

Q(fx,gy,gz)≤aQ(x,y,z)+bQ(x,fx,fx)

和

Q(gx,fy,fz)≤aQ(x,y,z)+bQ(x,gx,gx)

对于所有可比较的x,y,z∈X均成立.

则f和g有唯一的公共不动点x′∈X, 如果v=fv=gv, 则Q(v,v,v)=θ.

证明 对∀x0∈X,{xn}⊂X, 作如下定义

x2n+1=fx2n,x2n+2=gx2n+1

对于所有的n≥0 均成立. 因为f和g是弱增的, 则我们有

x1=fx0≤gfx0=gx1=x2且x2=gx1≤fgx1=fx2=x3

继续这个过程, 我们可以得到

Q(x2n+1,x2n+2,x2n+2)=Q(fx2n,gx2n+1,gx2n+1)≤aQ(x2n,x2n+1,x2n+1)+bQ(x2n,fx2n,fx2n)= (a+b)Q(x2n,x2n+1,x2n+1)

令h=a+b<1, 并结合以上不等式, 同理可得

Q(x2n+2,x2n+3,x2n+3)≤hQ(x2n+1,x2n+2,x2n+2)

因此, 显然有连续不等式

Q(xn,xn+1,xn+1)≤hQ(xn-1,xn,xn)≤…≤hnQ(x0,x1,x1)

设m>n, 则由定理1中的证明过程, 我们可以看出

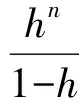
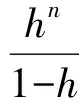
又由条件2), 我们有

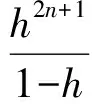
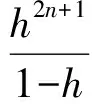
我们知道

Q(x2n+2,fx′,fx′)=Q(gx2n+1,fx′,fx′)≤aQ(x2n+1,x′,x′)+bQ(x2n+1,gx2n+1,gx2n+1)=aQ(x2n+1,x′,x′)+bQ(x2n+1,x2n+2,x2n+2)

而且

Q(x2n+1,fx′,fx′)≤Q(x2n+1,x2n+2,x2n+2)+Q(x2n+2,fx′,fx′)≤Q(x2n+1,x2n+2,x2n+2)+aQ(x2n+1,x′,x′)+bQ(x2n+1,x2n+2,x2n+2)= (b+1)Q(x2n+1,x2n+2,x2n+2)+aQ(x2n+1,x′,x′)

类似上述方法, 我们可以得到Q(x2n+2,fx′,fx′)≪c, 而且Q(x2n+1,fx′,fx′)≪c, 进而Q(xn,fx′,fx′)≪c, 又因为Q(xn,x′,x′)≪c, 故G(fx′,x′,x′)≪c或者G(x′,fx′,fx′)≪c, 从而fx′=x′ .

同理可得gx′=x′ , 则有fx′=gx′=x′ , 即x′ 为f和g的公共不动点.

如果v=fv=gv, 则

Q(v,v,v)=Q(fv,gv,gv)≤aQ(v,v,v)+bQ(v,fv,fv)=(a+b)Q(v,v,v)

因a+b<1 , 故Q(v,v,v)=θ显然成立.

下证唯一性.

若存在另一公共不动点y′, 使得fy′=gy′=y′ , 则有

Q(fx′,gy′,gy′)≤aQ(x′,y′,y′)+bQ(x′,fx′,fx′)≤aQ(x′,y′,y′)

和

Q(fy′,gx′,gx′)≤aQ(y′,x′,x′)+bQ(y′,fy′,fy′)≤aQ(y′,x′,x′)

因a<1 , 故Q(x′,y′,y′)=θ且Q(y′,x′,x′)=θ, 由引理5, 我们有

x′=y′

唯一性得证, 证毕.

注3 在定理2的证明过程中, 我们去掉了映射f的连续性, 也未用到文[9]定理3.2中的正规性以及iii)等条件, 取而代之, 直接运用我们引入的广义c距离中条件3)、4) 来得到想要的结果. 最重要的是, 我们在定理2中还引入了公共不动点唯一性的证明方法, 这一点, 在其他相关文献中几乎没有被研究过, 尤其要说明的是, 唯一性的证明方法借助了我们所提出的一个新的引理, 该引理的提出也是本文的亮点之一.

[1]Mustafa Z,Sims B. A new approach to gneneralized metric spaces[J]．Nonlinear and Convex Anal, 2006,(7): 289～297.

[2]Beg I, Abbas M,Nazir T.Gneneralized cone metric spaces[J]． J Nonlinear Sci Appl, 2010,(3): 21～31.

[3]Rao K P R, Lakshmi K B,Raju V C C.A unique common fixed point theorem for three mappings in G-cone metric spaces[J]． The Journal of Mathematics and Computer Science / TJMCS, 2012,(4):585～590.

[4]Ozturk M,Basarr M. On some coincidence and common fixed point theorems in G-cone metric spaces[J]． Thai Journal of Mathematics, 2011,9:647～657.

[5]李 颖, 宋眉眉. 广义锥度量空间的广义度量化[J]. 天津理工大学学报, 2012,28(3):7～9.

[6]Dordovic M,Doric D,Kadelburg Z,et al.Fixed point results under c-distance in tvs-cone metric spaces[J]． Fixed Point Theory and Applications, 2011,29: 1～9.

[7]Wang S, Guo B. Distance in cone metric spaces and common fixed point theorems[J]．Applied Mathematics Letters, 2011,24 :1735～1739.

[8]Sintunavarat W,Cho Y J,Kumam P.Common fixed point theorems for c-distance in ordered cone metric spaces[J].Computers and Mathematics with Applications. 2011(62): 1969～1978.

[9]Cho Y J,Saadati R,Wang S H.Common fixed point theorems on generalized distance in ordered cone metric spaces[J]．Computers and Mathematics with Applications, 2011,61: 1254～1260.

[10]Fadail Z M,Ahmad A G B,Radenovi S.Common fixed point and fixed point results under c-distance in cone metric spaces[J]．Applied Mathematics & Information Sciences Letters, 2013,2: 47～52.

Fixedpointtheoremsongeneralizedc-distanceinG-conemetricspaces

CAO Xiao-shuang,LIN Cun-jin, LIU Wei

(College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China)

In this paper, we generalize the main results which are shown by Yeol Je Cho, Reza Saadati and Shenghua Wang, and present the concept of generalizedc-distance. Subsequently, we will apply it intoG-cone metric spaces to solve the relevant fixed point theorems, in the process, we omit the continuity of operators, normality of cone and so on. Compared to previous one, our method may be more perfect to a large extent.

generalizedc-distance;G-cone metric spaces; fixed point theorems

2013—12—28

湖北省教育厅重点科研项目(D20102502)

曹小双(1988— )，女，湖北钟祥人，硕士研究生，主要从事非线性泛函分析的研究.

O177.97

A

1009-2714(2014)02- 0040- 06

10.3969/j.issn.1009-2714.2014.02.010