基于有限元裂缝网络的压裂液滤失模拟

2014-08-24李勇明刘鹏

石油天然气学报 2014年9期

关键词：滤失工作液压力梯度

李勇明,刘鹏

赵金洲,罗攀 (油气藏地质与开发工程国家重点实验室(西南石油大学),四川成都610500)

基于有限元裂缝网络的压裂液滤失模拟

李勇明,刘鹏

赵金洲,罗攀 (油气藏地质与开发工程国家重点实验室(西南石油大学),四川成都610500)

压裂液滤失速度是水力压裂设计分析中的重要参数之一,对于裂缝性储层,它可以用裂缝型储集层压裂液滤失数学模型来计算,但是现有的压裂液滤失数学模型并没有考虑天然裂缝呈不规则网络分布且形态复杂这些因素对滤失的影响。因此,在考虑这些因素的前提下,以压裂液沿着天然裂缝向基质渗滤为基础,建立了裂缝网络的等效连续介质滤失模型,运用有限元方法求得了数值解。新方法能模拟复杂裂缝形态对滤失过程中压力分布的影响,克服了传统方法不能模拟裂缝弯曲、相交、方位变化等对滤失影响的局限。

天然裂缝;压裂液;裂缝网络;有限元;滤失模型

水力压裂施工中,被泵入到地层中的压裂液在裂缝与地层的压力差作用下会向地层发生滤失,其滤失量的大小将直接影响压裂液的效率、裂缝几何尺寸和压后支撑剂在裂缝中的分布。对此,许多学者也曾提出过相关的滤失模型[1,2]来研究压裂液滤失,但将天然裂缝考虑进来的却很少。天然裂缝的存在可导致液体滤失量成倍增加,难以形成严格意义上的滤饼区,传统的这些滤失模型就不适合用于天然裂缝较发育的地层滤失。针对天然裂缝的影响,李勇明等[3,4]建立了考虑裂缝型储集层压裂液滤失的数学模型,并给出了模型的解析解,但也未涉及到天然裂缝呈不规则网络分布、形态复杂等因素的影响。为此,笔者通过引入裂缝渗透率张量表达式,然后运用有限元方法建立了考虑裂缝呈不规则网络分布的等效连续介质滤失模型,最后模拟裂缝形态,分析了各种复杂的、不规则的呈网络状分布的裂缝对压裂液滤失的影响,为天然裂缝较发育的裂缝型储层进行压裂设计与施工提供了一定的参考价值。

1 裂缝渗透率张量的引入

假设在地层中有一条天然裂缝,其缝宽为w,流体在其中流动时遵循达西定律。根据流体力学理论,通过间距为w的两个单位高度的平行板间的流体平均流量与压力梯度的关系为[5]:

式中:Q为流体流量,cm3/s;μ为流体黏度,m Pa·s;w为裂缝宽度,10-1mm;p为裂缝中流体压力, 10-1MPa;l为裂缝长度,cm。

达西定律中流量与压力梯度的关系可表示为:

式中:K为裂缝渗透率,D;A为横截面积,cm2。

结合式(1)、(2),可得沿平行板方向的等效渗透率:

由于天然裂缝一般很窄,垂直于裂缝方向上的流动范围十分有限;基质渗透性决定了裂缝中垂直于壁面的渗流,因此可以认为垂直于裂缝壁面方向的等效渗透率就是基质渗透率。即:

渗透率是一个二阶张量,二维情形下共有4个分量,以矩阵的形式表示为:

式中:Kxx、Kxy、Kyx、Kyy为渗透率张量的4个分量,D。

当裂缝方向与压力梯度方向之间的角度为θ时,渗透率张量可表示为:

由式(5)、(6)可见,不论θ取何值,渗透率二阶张量中有一对分量是相等的,即Kxy=Kyx。此时渗流方向与压力梯度方向也不一致,渗流速度按坐标轴分解为vx和vy,渗流速度分量不仅与该方向上的压力梯度相关,还与垂向上的压力梯度相关,即:

式中:vx、vy分别为沿着裂缝方向和垂直于裂缝壁面方向的渗流速度,cm/s。

2 裂缝网络的等效连续介质滤失模型

天然裂缝的存在极大地影响滤失状况,尤其是当裂缝渗透率与基质渗透率差别较大的时候。研究含裂缝与基质的两种介质中工作液滤失或渗流是一个非常复杂的问题[6,7],尤其是需要考虑到天然裂缝的具体形态的时候。得益于有限元方法的出现,现在已经可以解决这一难题了。

前面给出了裂缝的等效渗透率,因此可以将含有裂缝的介质看成是连续介质,只不过连续介质的渗透率不是固定的,而是随位置变化的,并且为各向异性的,可表示为张量形式。具体说来,等效连续介质的渗透率主要分为2种:第1种是基质渗透率,一般可认为基质是各向同性的,其渗透率可以表示为Km,表示为张量的形式为:

第2种是裂缝渗透率,裂缝的渗透率张量为K(θ),它与裂缝的开度、裂缝与基质的角度等相关。裂缝与基质共同组成了渗流区域[8～10],因此,等效连续介质滤失模型所要考虑的就是在不同位置取不同的渗透率张量进行计算。

已知连续介质渗流的质量守恒方程为:

式中:C为地层综合压缩系数,MPa-1;t为滤失时间,s。

将式(7)、(8)代入式(11),可得连续介质滤失模型:

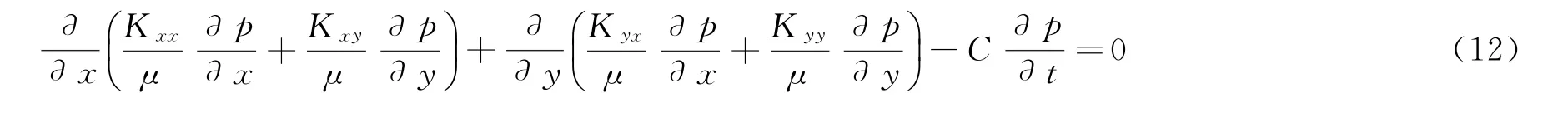
即:

根据连续介质的滤失模型方程 (12)与内外都定压的边界条件,运用有限元理论可写出方程的弱形式为:

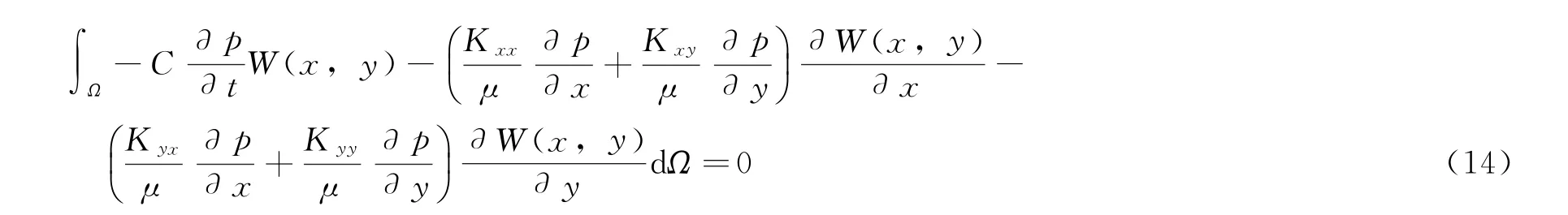
式中:W(x,y)是有限元插值函数;dΩ表示在整个滤失区域积分。

将上述弱表达式写入COMSOL软件,便能通过有限元方法求解网络裂缝的等效连续介质滤失模型方程。

3 天然裂缝形态对滤失的影响

3.1 裂缝方向

地层中天然裂缝方向与工作液流动压力梯度方向 (即滤失方向)之间的夹角会直接影响到滤失速度的大小。根据式 (14)运用有限元方法得到了滤失区压力分布的数值解,如图1所示。

图1 不同方向的天然裂缝对滤失区压力分布的影响

图1为模拟区域含3种不同方向天然裂缝,与压力梯度方向分别为0°、-45°、90°,滤失时间均为3000s。从数值计算结果来看,裂缝方向对滤失存在着不同程度的影响,顺着压力梯度方向的裂缝能大量增加压力传播速度和滤失速度,而垂直于压力梯度方向的裂缝几乎没有影响,角度在二者之间的裂缝的影响也介于二者之间。因此可以认为当油藏中顺着压力梯度方向的天然裂缝条数越多,工作液的滤失也越快。

3.2 裂缝密度

地层某一区域中天然裂缝条数分布越多,工作液流入该区域所需的阻力越小,工作液滤失量也就增大。利用式 (14)并结合有限元方法模拟了在3种不同裂缝密度条件下滤失区域的压力分布等值线,结果如图2所示。

图2 不同裂缝密度的天然裂缝对滤失区压力分布的影响

图2(a)为边长5m的矩形,图2(b)为边长2m的矩形,图2(c)为边长1m的矩形,滤失时间均为3000s。由模拟结果可见,天然裂缝越密,从裂缝到油藏深部的压力传播越快,滤失速度也越快。由此可认为油藏岩石天然裂缝越发育,则工作液滤失速度越快。

3.3 裂缝宽度

式 (3)已经给出顺裂缝方向的裂缝渗透率与裂缝宽度的关系式,这里具体研究不同裂缝宽度对滤失的影响。表1是在给定的裂缝宽度下,由式(3)计算出的对应等效渗透率。

由式(3)可知,裂缝渗透率与裂缝宽度的平方成正比,所以裂缝宽度对滤失速度有平方次数的影响,对滤失量则存在立方次数的影响,裂缝宽度对滤失的影响非常大。图3分别模拟天然裂缝在给定的宽度、长度下运用有限元方法求解方程 (14)得到的滤失区压力分布与滤失速度分布数值解。图3(a)中上边的裂缝宽度为0.01mm,中间裂缝宽度为0.005mm,最下边裂缝宽度为0.001mm。由图3可见,天然裂缝宽度还很大程度地影响了基质中的压力分布。可认为,油藏中存在较宽天然裂缝时,工作液滤失将显著增加。

表1 不同宽度的裂缝对等效渗透率的影响

图3 天然裂缝对滤失区压力分布与滤失速度的影响

3.4 裂缝长度

图3(b)中天然裂缝长度从上到下依次为8、6、4、2m。由模拟结果可见,天然裂缝长度对基质的压力分布影响较大,长裂缝附近基质压力等值线推进的速度更快。由此可预测长裂缝中的滤失速度更大。图3(b)右边区域是天然裂缝中的工作液滤失速度,长裂缝中的滤失速度明显大于短裂缝的滤失速度,这是因为长裂缝需要向更多的基质供液。另外裂缝口的滤失速度远大于裂缝深部的滤失速度。

3.5 裂缝连通性

天然裂缝连通性对工作液滤失存在很大影响,在天然裂缝连通性较差的储层中工作液滤失时,需要通过渗透率较低的基质,这相当于增加了工作液滤失的阻力,而在裂缝连通性好的储层中的滤失阻力小,滤失明显要快得多。考虑同一区域中天然裂缝呈不同连通性条件下,运用有限元方法求解式 (14)得到该滤失区域压力分布的数值解。

从图4模拟结果可见,连通性好的储层中压力等值线推进速度大大高于连通性差的储层,说明工作液在连通性好的裂缝中越容易流动,滤失量会相应增大。