t-NIG单因子Copula的CDO定价模型
2014-08-24,,,
, , ,
(浙江工业大学 理学院,浙江 杭州 310023)
CDO定价的核心问题是参考资产投资组合损失分布的计算,首先必须研究资产的违约相关性.一般的相关性结构只能用Monte Carlo进行模拟,而CDO定价中相关性研究常运用因子Copula方法,假设信用资产池的各资产与公共市场因子相互独立,再通过半解析方法计算累计损失分布[1].2003年Laurent和Gregory[2]提出了快速Fourier转换方法,2003年Sidenius和Basu[3]以及2004年Hull和White[4]都研究了迭代数值过程计算参考资产池的损失分布.更进一步假设真实的参考信用投资组合是由大量具有相同违约率,回收率和相关系数的资产组成,在这种假设条件下,可以得到一个封闭式的CDO解析定价公式.1987年Vasicek根据大数定律提出LHP近似方法[5-6].在前人研究基础上分析了大样本同质投资组合(LHP)近似方法下基于t-NIG单因子Copula的CDO定价模型,这个定价模型事实上是CDO标准定价模型(单因子Gaussian Copula)的扩展延伸.对模型的扩展正是为了解决标准Gaussian Copula缺乏“厚尾性”和存在“相关性微笑”这两个方面的问题,使定价和市场报价更好的吻合.许多研究者试图采用尾部相关性更强的因子Copula模型来定价CDO,例如,2005年Andersen和Sidenius[7]提出的Marshall-Olkin Copula;2003年O’Kane和Schloegl提出的Student t Copula;2004年Hull and White[4]提出的double t Copula等.论文通过double t,正态逆高斯(NIG)[5]单因子Copula模型分别对Dow Jones iTraxx Europe指数的各分券层定价.除这些模型外,文中基于t-NIG单因子Copula模型在LHP下对CDO定价进行更详尽的研究.另外,论文分析了数值结果,对不同模型适应CDO各分券层的市场报价的能力进行比较.结果表明:所有的模型都比标准模型更好地适应市场报价,新型模型定价效果最为理想.
1 CDO分券层的半解析定价
合理给定CDO不同分券层的信用价差即是CDO定价.每个分券层可分为损失面(DL)和收益面(PL),损失面是指投资分券层违约发生时的损失现值,收益面是指投资分券层违约发生时的收益现值,根据无套利原则,通过损失面和收益面相等,得出不同分券层合理的信用价差,进行CDO定价.

(1)
其中时刻t的累积损失L(t)可表示为
(2)
为了能基于t-NIG单因子Copula模型研究CDO定价,在此引入引理1[5]和引理2[5].
引理1设时刻t的累积损失分部函数为F(t,x),CDO中(K1,K2)层的期望损失百分比可表示为
EL(K1,K2)(t)=
(3)
下面描述常用CDO定价半解析方法中CDO各分券层(K1,K2)的损失面(DL),收益面(PL)和信用价差S的计算.分券层(K1,K2)损失面的价值DL为违约支付贴现值[5],表示为
(4)
分券层(K1,K2)收益面的价值PL为所有支付的权利金的现值[5],表示为
(5)
式中Δti=ti-ti-1,i=2,…,M.
根据无套利原则,通过损失面和收益面相等,从而得到不同分券层的合理信用价差S.
引理2在无套利的情况下,CDO各分券层的定价公式为
(6)
资产的回收率,资产间的相关性和违约率是影响信用价差的主要因素:
1) 当资产的市场回收率增加时,各分券层的信用价差减少,高级分券层受回收率的变化影响相对较小,股本分券层的信用价差受其影响最大.
2) 当资产的相关性增强时,参考资产池发生联合违约的可能性增大.
3) 当资产的违约率增加时,各分券层的信用价差都增加,违约强度对股本分券层影响最深.
2 LHP情况下的t-NIG单因子Copula模型
引理2中给出了CDO信用价差的计算公式,为了能通过公式数值计算出信用价差S,本节通过构建t-NIG单因子Copula模型将单个公司资产的违约概率转化为非系统因子的违约概率问题计算资产的条件违约概率,进一步在LHP的假设条件下近似计算出参考资产投资组合损失分布,最终结合引理1,2确定信用价差S.
2.1 t-NIG单因子Copula模型
为了捕捉金融市场的“厚尾性”的特征,研究者试图用厚尾分布来建立金融市场模型.NIG分布是正态分布和逆高斯分布的混合厚尾分布,具有与金融市场研究相关的优良统计性质.NIG分布的尾部比标准高斯分布下降的更缓慢[9],并通过调节NIG分布的四个灵活参数,使其更能充分反映金融市场中参考资产池的“尖峰厚尾”特征.且NIG分布有稳定的卷积性,使计算更有效快速.在构建t-NIG单因子Copula模型之前,下面先了解正态逆高斯分布的定义及其有关性质[5].
定义1NIG分布是正态分布和逆高斯分布的混合分布.若随机变量U服从参数为α,β,μ和δ的NIG(α,β,μ,δ)分布,则其密度函数为
fNIG(x;α,β,μ,δ)=
(7)

性质1若随机变量U~NIG(α,β,μ,δ),则

金融市场数据一般具有明显的厚尾性,如果CDO定价模型中分布尾部太薄,没有厚尾性特征,得出的信用价差就会与市场报价相差过大,导致CDO各分券层的相关系数存在“相关性微笑”现象.CDO定价的标准模型(单因子Gaussian Copula模型)正是如此.因此,在因子Copula模型中,可以选取更具有“厚尾性”的潜在因子变量来代替高斯因子变量,更好地体现CDO参考资产池损失的“尖峰厚尾”性.因而,假定市场共同因子和个体异质因子分别服从t分布和NIG分布,得到新的t-NIG单因子Copula模型.下面给出t-NIG单因子Copula模型的具体定义和相关定理.
定义2假定CDO资产池中标的资产i的资产价值xi满足
(8)
式中:ρi∈[0,1]为系统因子Z与资产价值xi之间的相关系数;Zi为影响资产i价值的非系统因子.随机变量Z与Zi及Zi与Zj(i≠j)间相互独立,且市场共同因子Z和个体异质因子Zi分别服从学生t分布和NIG分布[10]:
Z~T(x;ν)
(9)
Zi~FNIG(x;α,β,μ,δ),i=1,2,…,n
(10)
称由式(8—10)确定的模型为t-NIG单因子Copula模型,简称t-NIG Copula模型.根据性质1,把非系统因子Zi标准化.用参数α,β表示参数μ,δ:
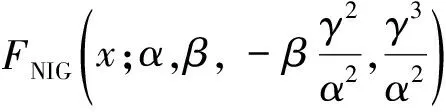
定理1若CDO资产池中标的资产i的资产价值xi满足t-NIG Copula模型,设Hi(x)为资产价值xi的概率分布函数,则
Hi(x)=
(11)
证明由定义2可知资产价值xi的条件概率:
对条件概率积分,得到无条件概率分布函数为
Hi(x)=P(xi 定理2若CDO资产池中标的资产i的资产价值xi满足t-NIG Copula模型,则资产i的条件违约概率为 (12) 即 令 si(t)=P(τi≥t)=1-qi(t) (13) 由式(13)可得 (14) (15) 又根据t-NIG Copula模型,可以将单个公司资产的违约概率转化为非系统因子的违约概率问题,因此 (16) (17) 对F(t,x)微分,则 dF(t,x)= (18) 令 (19) 可知 (20) 由式(18—20)得 (21) 将式(19,21)代入引理1的式(3)进行换元代换,则 (22) 根据式(22)和引理2,我们可以基于t-NIG Copula模型应用LHP近似方法定价CDO.考虑信用衍生品指数Dow Jones iTraxx Europe指数2006年4月13日的各分券层报价.投资组合平均价差为31.5 bp,选取2006年3月20日设立的5年期指数系列,利用常数违约强度模型来获得边际违约分布,并估计在平均投资组合价差下大样本同质投资组合的违约率.回收率和无风险利率各自假定为40%和5%.下面选取标准Gaussian Copula模型,Double t Copula模型,NIG Copula模型,t-NIG Copula模型,在LHP情况下,给出数值分析结果.运算结果见图1,2和表1. 图1为Gauss分布、t分布、NIG分布的概率密度函数曲线以及左右尾部比较,其中t分布尾部最厚,NIG分布尾部较Gauss分布尾部更厚,但比t分布尾部薄,“尖峰”特征最为明显,t-NIG单因子Copula模型结合了两种分布的优势,使其充分体现了CDO参考资产池损失分布的“尖峰厚尾”特征.图2比较了四个模型的累积损失分布函数,能够反映模型的“相关性微笑”问题以及贴合市场报价能力.可以通过观察其各累积损失分布尾部的不同形状对表1中各模型的数值结果加以解释.表1为iTraxx各层的市场报价以及Gaussian Copula,Double t Copula,NIG Copula,t-NIG Copula的LHP模型适应市场报价能力的比较,并依据参数校准原则:股本层定价与市场报价相符以及各分券层定价的平方误差和达到最小,将四个模型中参数进行校准,结果表明:Gaussian Copula远远高估了3%~6%这个分券层的价格,其他模型在这个分券层的定价都与市场报价匹配相对较好;反之,却低估了高级分券层,这都是由于Gauss分布的尾部太薄的缘故.Double t Copula仅仅能精确定价CDO股本层,而高估或低估CDO其他分层券,因为Double t Copula只有一个连续参数(相关系数),而另一个参数ν(自由度)只能取整数值.由于NIG Copula,t-NIG Copula中的自由参数比Double t Copula更多,它们的所有结果比Double t Copula的所有结果都稍好,甚至能精确定价CDO的第二分券层.且t-NIG Copula模型很好地提高了NIG Copula模型定价的精确性,误差由原来的22 bp缩小到8.5 bp.原因是该模型引入了更能反映金融市场特征的t-NIG Copula,改进了经典的Gaussian Copula模型,所以定价精度更高,更能改善“相关性微笑”问题. 图1 三种分布密度函数比较 图2 四种模型的累计损失分布函数比较 表1 各模型适应CDO各分券层的市场报价能力比较 对Gaussian Copula模型进行扩展,构建了t-NIG Copula模型用于CDO定价.得到了条件违约概率,投资组合损失的累积分布函数,期望分券层损失和信用价差的表达式.t-NIG Copula模型相对于研究的其他模型有更多的自由参数,给相关性结构带来更多的灵活性,因而也更能贴合CDO的市场报价.另外, t-NIG Copula模型改善了Double t Copula是无卷积稳定性的缺点,这样就简化和加速了违约阈值的计算,实际应用性更强. 参考文献: [1] 马岩.组合信用衍生品的定价模型及数值算法研究[D].天津:南开大学,2008. [2] LAURENT J P, GREGORY J. Basket default swaps, CDO’s and factor Copulas[J]. Risk,2005(7):103-122. [3] ANDERSEN L, SIDENIUS J, BASU S. All your hedges in one basket[J]. Risk,2003,16(11):67-72. [4] HULL J, WHITE A. Valuation of a CDO and an n-th to default CDS without a monte carlo simulation[J]. Journal of Derivatives,2004,12:8-23. [5] KALEMANOVA A, SCHMID B, WERNER R. The normal inverse gaussian distribution for synthetic CDO pricing [J]. Journal of Derivatives,2007,14(3):80-94. [6] 陈剑利.基于因子Copula的CDO定价模型[D].杭州:浙江大学,2012. [7] ANDERSEN L, SIDENIUS J. Extensions to the Gaussian Copula: random recovery and random factor loadings[J]. Journal of Credit Risk,2005(1):29-70. [8] 陈田,秦学志.债务抵押债券(CDO)定价模型研究综述[J].管理学报,2008,5(4):616-624. [9] 陈田,秦学志.基于因子Copula的债务抵押债券定价模型研究[D].大连:大连理工大学,2010. [10] 朱齐飞,李锋.基于t-NIG分布单因子模型的抵债务证券(CDO)定价研究[D].昆明:云南师范大学,2008. [11] LI D X. On default correlation: a Copula approach[J]. Journal of Banking and Finance,2000,9(4):43-54.



2.2 t-NIG因子Copula模型的LHP近似
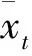

3 数值分析



4 结 论
