多态性作业车间鲁棒调度CA-GA建模

，，，

(浙江工业大学 机械工程学院,浙江 杭州 310014)

随着竞争的日益激烈，企业面临多样化、快速化的挑战，其生产过程在订单、设备、工艺、批量等层次上越来越凸显出形态和状态的多样性，生产调度的柔性、鲁棒性和动态性需求逐步增加[1].由此，越来越多的企业采用订单驱动、多功能设备、多品种、多工艺及中大变批量的多单元作业车间方式.Goutam Satapathy将此类企业作业车间归纳为“多态性作业车间”[1].多态性作业车间加工批量和运转批量呈现多样性和动态性，生产过程离散度高，大规模定制下生产计划与排产日趋复杂.现有研究表明：单一的优化算法已无法满足生产作业车间调度难点，两种或两种以上方法的结合成为当前研究的新趋势，如混合算法、仿真模型嵌套算法等.鞠全勇等[2]结合多种群粒子群搜索与遗传算法的优点提出具有倾向性粒子群搜索的多种群混合算法，提高了搜索效率和质量，很好地解决了多目标批量生产车间优化调度问题.刘爱军等[3]提出基于混合再调度策略的自适应遗传算法，不但能同时优化工艺路线和加工顺序，还能实现实时动态调度功能，有效解决了柔性作业车间多目标动态调度问题.Nasr和EIMekkawy[4]根据设备随机故障的情况，基于最坏情况来建模，结合混合遗传算法解决柔性作业车间调度问题的鲁棒性和稳定性.

元胞机由Von Neumann提出，具有强大的空间运算能力，并有离散性、并行性等特点，已应用于材料、交通运输和城市规划等研究领域[5-7].阮幸聪等[8]运用元胞机建模，构建大型机械构件生产车间的柔性调度仿真模型.由于多态性作业车间鲁棒调度具有高度复杂性、动态性和不确定性等特点，其个体行为按固定的简单规则演变来描述已经不合适.由此，选用遗传算法来优化元胞机的演化规则，建立多态性作业车间鲁棒调度CA-GA模型以获得更优的调度方案.

1 多态性作业车间元胞机鲁棒调度模型建立

元胞机模型是对客观世界抽象的结果，结合元胞机自身的结构特点，构建多态性作业车间鲁棒调度CA框架.标准元胞机由元胞、元胞空间、邻域和局部演化规则构成，模型表达式为As={L2,S,N,R,Fs}，式中：As为多态性作业车间调度系统元胞机模型；L2为二维网格机构；S为工位元胞的状态；N为领域元胞的状态；R为约束条件；Fs为调度规则.可以以工位表示元胞个体，工件代表移动粒子，工件到达系统的节拍表示初始和入口边界条件，调度规则作为演化规则来描述多态性生产系统二维网格空间.

1.1 二维网络结构

车间调度的元胞机模型的二维网络结构是根据多态性作业车间调度的特点而设计的.如图1所示，每个网格作为一个元胞，代表一个加工工位.该网格系统每一行代表多个同类性质的工位，称为单元组.格点之间的有向连线即运输作业路线.

图1 生产车间元胞机模型网格图

任一格点在τ+1时刻的状态可以一般性地描述为

Sτ+1=f(C,Sτ,N,R)

(1)

式中：τ为作业时间；C为元胞空间；S为元胞状态；N为邻域元胞；R为约束条件；f为调度规则.元胞机中，其演化规则是局部的，对指定元胞的状态更新只需知道当前元胞状态及其领域元胞的状态，以及所遵循的规则即可.模型中定义某工位元胞的领域元胞为其上下游单元组中的所有工位元胞.

1.2 基本演化规则

演化规则是模型的关键部分，根据多态性作业车间调度的特点将本模型的自组织演化规则归纳为以下三条，如表1所示.

表1 模型演化规则

1.3 鲁棒调度多目标函数

考虑到调度的鲁棒性，模型在最初产生调度方案时将设备故障考虑进去，另一方面实行在线动态决策.动态决策主要反映在再调度中，模型中将考虑插单工件的情况.另外，采用Leon等[9]对于鲁棒性调度的思想，将最大完成时间作为目标函数的组成部分，而平均松散时间则作为对各个方案的评价指标.

多态性作业车间鲁棒调度具有多目标性，因而为多目标调度问题的研究.根据作业车间多品种小批量的特点，加工时间的长短是首要考虑因素；为了保证客户满意度，交货期也非常重要，因此需考虑延期交货的问题；为了实现均衡化生产，还应考虑各设备负荷的平衡率.结合以上实际情况，选用的最优目标有加工总时间∑Ti、最大延迟Lmax和设备平衡率Rlb这三个，其目标函数为后面运算方便均进行了统一：

1) 工件所有工序最大完成时间最短，即

(2)

2) 工件的最大延迟最小，即

(3)

3) 各工位设备平衡率高，即

(4)

通过权重加和法，元胞机每个离散单元在每个时步内的调度多目标函数为

F=max(w1F1+w2F2+w3F3)

(5)

采用传统的优先权值设定法，事先设置各个目标值的优先权值，分别根据前面3个子目标函数的重要性设置权重值，得到：w1=0.4，w2=0.3，w3=0.3.

车间调度系统约束条件如下：

1) 工艺约束条件：

stij≥eti(j-1)i=1,2,…,n；j=1,2,…,m

(6)

2) 机器的能力约束条件：

stij≥et(i-1)ji=1,2,…,n；j=1,2,…,m

(7)

3) 工艺约束.工件在机器上加工时不能被打断，直至该工序加工完毕.

式(6，7)中：stij表示第i个工件的第j道工序的加工开始时间；etij表示第i个工件的第j道工序的加工结束时间.

2 遗传算法优化多态性作业车间元胞机模型

遗传算法是一种基于生物自然选择与遗传机理的随机搜索算法，具有良好的领域无关性，因而有很大的灵活性.本模型中，遗传算法用于寻找最优演化规则嵌套于元胞机模型中.根据这个算法过程反复迭代，直到满足终止条件，此时得到的染色体可视为经遗传算法寻优后得到的元胞机演化的最优规则.

2.1 演化过程

现将元胞机在每个时步的调度模型描述为：n个工件粒子需在具有m个同类工位的单元组中进行加工.其中，每个工位的加工效率不同，且在此单元组中每个工件只需完成一道工序，每道工序可供选择的工位根据实际情况可能是单元组中的几个或全部，在不同的工位上加工每道工序所需的时间不一.设：

2) 一个单元组内的工位集为s={s1,s2,…,sm}.

3) 工序Oij表示第i个工件的第j道工序.

以下面的算例来说明.已知，元胞机仿真模型的某个时步有6个工件pn，n=(1,2,…,6)进入2号单元组，该单元组有5台同类型的通用设备sm，m=(1,2,…,5)，5台设备的效率和性能均不相同.6个工件分别在5台设备上所需的加工时间，如表2所示，表2中，“—”表示工件pi无法在设备sj上加工，原因包括设备故障或是加工要求和设备性能不匹配等.

表2 设备加工时间表

算例对应的元胞机模型图如图2所示.

图2 算例元胞机模型图

2.2 遗传算法优化操作

2.2.1 染色体编码与解码

根据某一仿真时步内所有工序的加工工位和每个工位上的加工顺序，将调度编码分为工位染色体和工序染色体两个部分.两种编码融合后形成一条染色体，对应于时间、空间均离散的单元调度的一个可行解.

解码时，先由工位染色体来确定各道工序的加工工位，再根据工序染色体确定分到各个工位的工序的加工顺序.结合所有静态调度单元的调度方案，可获得元胞机所模拟的整个车间的调度方案.且整体调度方案随着仿真时步的推进将做出实时更新，考虑扰动因素，从而增加系统模型的鲁棒性.

2.2.2 初始种群生成

由于该染色体包含两个部分，对于收敛速度要求高，因此不采用随机初始化方法，而是直接以min(wl÷pe)为标准获得工位选择方案，及根据FCFS规则结合工件加工优先级获得排序方案，得到遗传算法的初始解.在获取初始解过程中，设置一个设备时间数组来记录每个工位的累计作业时间.初始化状态时，该数组的元素值均为0，因此第一个工件可直接选择加工时间最短的设备，然后将加工时间加到设备时间数组对应的元素上.如算例中按照p1-p2-p3-p4-p5-p6的顺序选择工位，其中一个工位初始解为5-4-3-2-2-1，对应加工设备s5-s4-s3-s2-s2-s1.具体操作过程如图3所示.

图3 算例初始解获取过程

2.2.3 适应度函数

鉴于适应度函数单值、连续、非负、最大化，合理、一致性、计算量小以及通用性强等特点，直接将目标函数设为适应度函数，即

(8)

2.2.4 选 择

2.2.5 交 叉

将染色体分为两个部分，工位染色体直接采用双切点交叉法，随机选择两个切点，交换两个切点之间的字串.工序染色体中，由于每道工序只能出现一次，考虑到染色体的合法，要求一个个体的染色体编码中不出现有重复的基因码.因此，工序排序染色体的交叉选用部分匹配交叉(PMX)操作，先随机选取两个交叉点，然后交换两个父代个体中交叉点之间的中间段，最后根据中间段给出的映射关系来生成两个子个体.

例如，下面是两个父代个体的基因码，随机选取两个交叉点“|”，即

p1：(1 2 3 |4 5 6| 7 8)

p2：(4 6 2 |1 8 3| 5 7)

首先，把两个交叉点之间的中间段互相交换，可得到

o1：(x x x |1 8 3| x x)

o2：(x x x |4 5 6| x x)

其中x表示目前未定义码，由上可得到中间段的映射关系，有：1→4，8→5，3→6.

然后，对于子代个体1，2中x部分，各自保留其父代个体中继承的未定义码2，7，可得到

o1：(x 2 x |1 8 3| 7 x)

o2：(x x 2 |4 5 6| x 7)

最后，根据上述中间段映射关系得到的子个体为

o1：(4 2 6 |1 8 3| 7 5)

o2：(1 3 2 |4 5 6| 8 7)

在映射关系中可能存在着传递关系，即备选交换码有多个，那么选择此前未确定的基因码作为交换.

2.2.6 变 异

变异可分为两个部分.第一部分为工位染色体的变异，在基因串中随机选择一个基因，在该工序的工位集中随机选取一个与其不等的整数，替换当前基因，保证可行解.第二部分为工序染色体的变异，采用基因位置互换的方法，这样保证了同一条工序排序染色体中不会出现相同的数字，保证可行解.

3 实例验证

3.1 实例描述

PTCN二厂生产电池包，整体布局复杂，产线规模各有不同，产品种类繁多，工艺复杂，是典型的多态性生产车间.以该车间为例，将其局部简化成一个元胞机模型，并把设备归类，按照多单元布局的方式，把各种设备简化成一个个单元组来布局.

在研究过程中，将生产过程进一步抽象，由于39种型号的产品都需要进行点焊，因此将点焊机这个单元组抽离出来，8台点焊机分别记为M1,M2,…,M8，它们同属于同一工位元胞单元组C11,C12,…,C18.由于各个单元组内调度情况相似，因此仅以一个单元组作为对象进行实例说明.表3为产品的订单信息.

表3 产品订单信息

同样的，交货期d也是根据每个不同的订单量确定的，这里的d主要指生产部分的交货期，详见表5.

考虑到设备故障造成的再调度情况，7，8，9月各设备故障率如表6所示.

表4 工件粒子初始状态属性表

表5 工件生产交货期

表6 第三季度设备故障率

3.2 仿真结果与分析

遗传算法参数设置：初始种群NP=10，交叉概率Pc=0.6，变异概率Pm=0.001，迭代次数80.

3.2.1 实际车间调度结果

实际上，车间进行调度的基本原则是以先到先生产进行的.订单到达后，选择可进行加工的设备，投入生产.订单陆续完成，后续订单随机选择空闲设备进行加工.图4为PTCN公司二厂电池包线点焊单元第三季度整季度订单式生产的实际调度甘特图.

3.2.2 调度及再调度

第一次调度进行实验21次，得到20个初始种群，每个初始种群分别经过适应度计算、选择、交叉和变异这几个步骤，循环80代，生成一个遗传算法优化后的解集，选取解集中的最优解作为第一次调度方案.根据8月份插单工件的情况，加之第一次调度未开始生产的工件，进行第二次调度.同上操作，得到第二次调度的优化方案.类似方法得到第三次调度的优化方案.优化后方案的甘特图如图5所示.

3.2.3 结果比较与评价

根据以上甘特图结果可以看出，遗传算法优化后的元胞机模型所得出的调度方案在加工总时间、设备利用率、设备平衡率等各个方面，全部优于原调度方案.具体对比情况可看柱状图，见图6—8.

图4 实际生产调度甘特图

图5 优化后调度甘特图

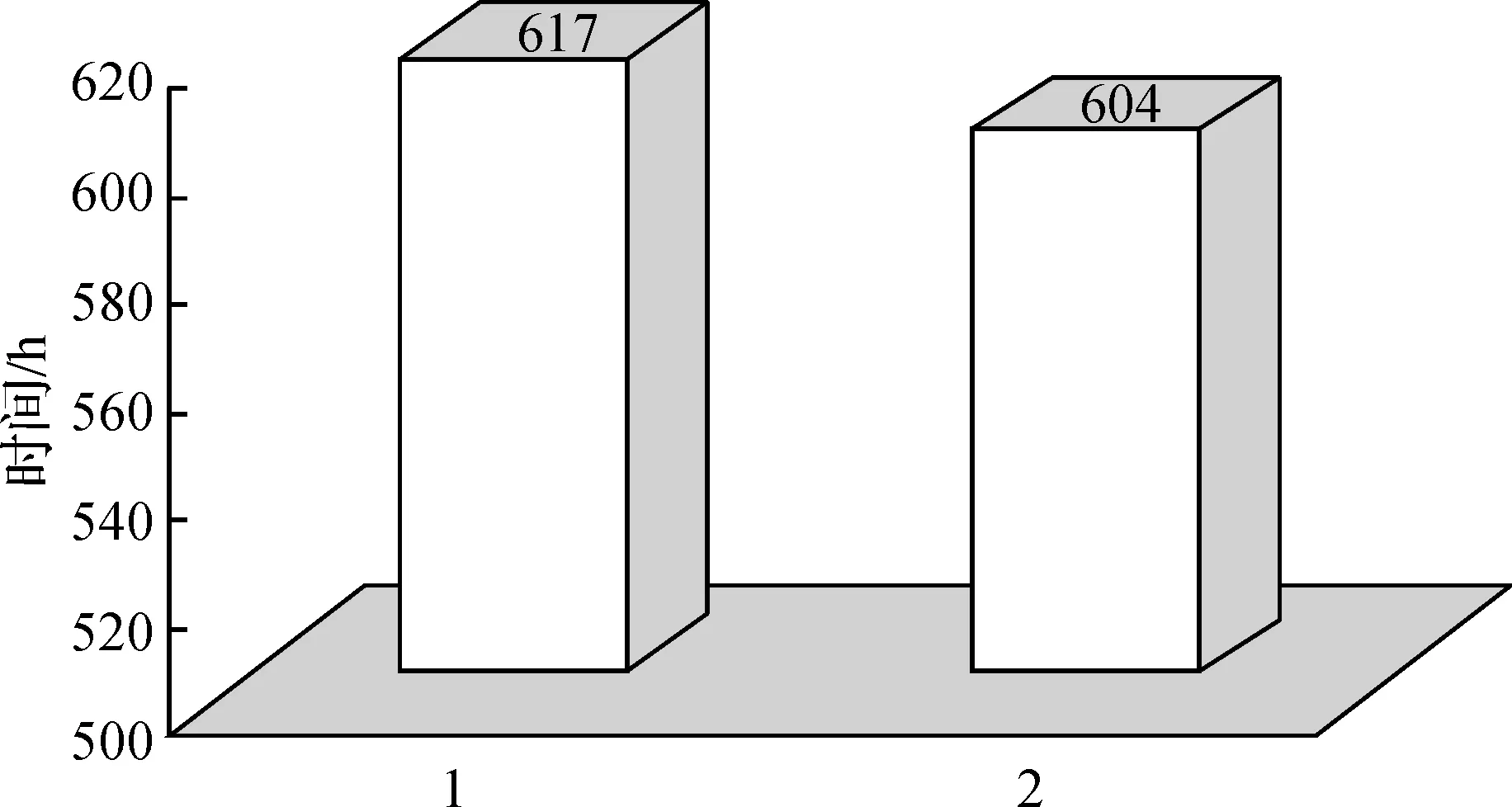
图6 优化前后加工时间对比

图7 优化前后设备利用率对比

(a) 优化前设备平衡率 (b) 优化后设备平衡率

根据平均松散时间的定义为

(9)

式中：tbi为工件i不超过最大完成时间的最晚开始时间；tai为工件的到达时间.平均松散时间值越大，说明调度方案抵抗干扰的能力越强，说明方案的鲁棒性越好.对三次调度分别计算平均松散时间，结果见表7.平均松散时间的值每经过一次再调度都会增加，说明再调度方案增强了系统的鲁棒性.

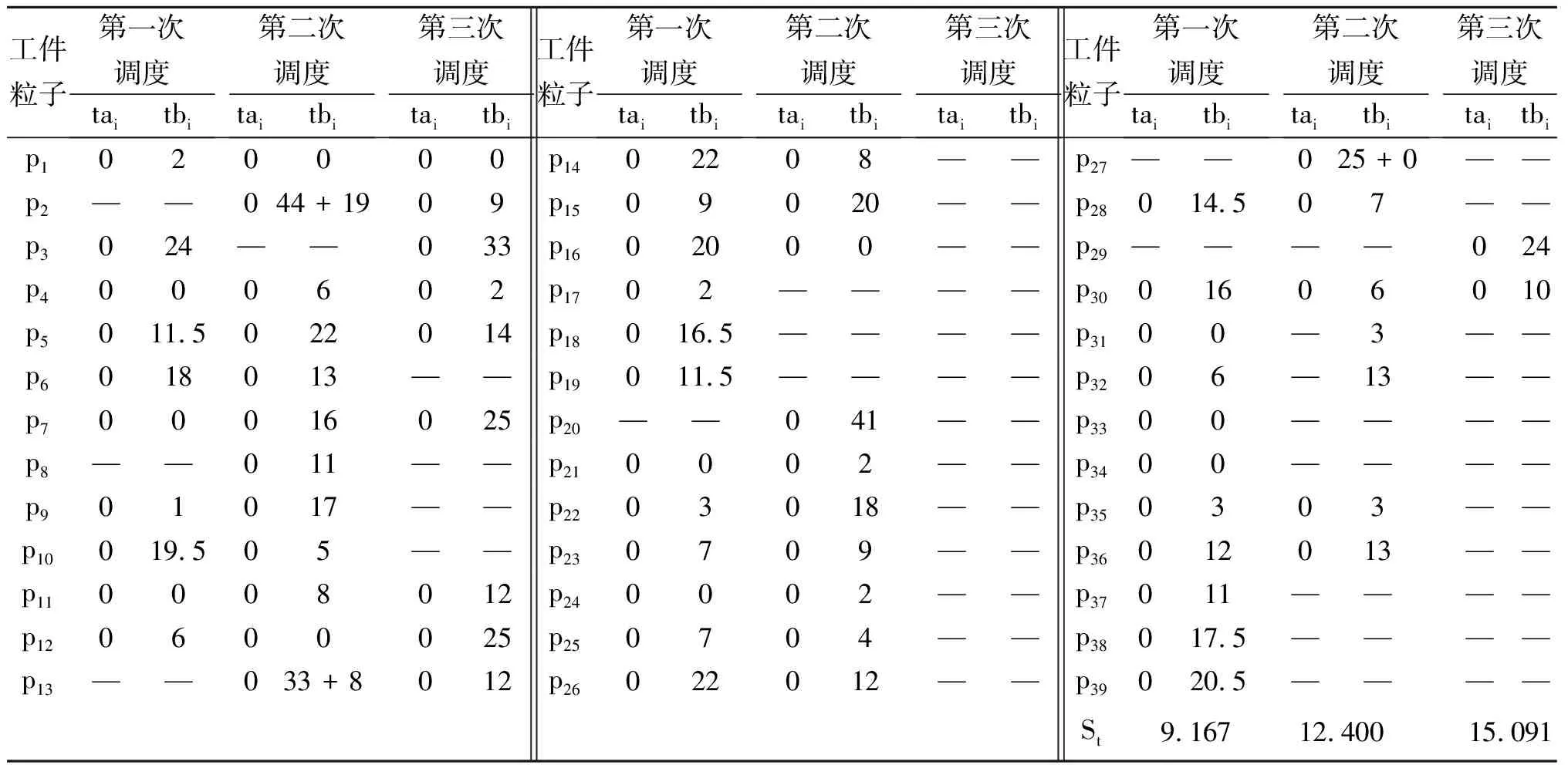
表7 平均松散时间计算表

4 结束语

针对多态性作业车间鲁棒调度问题建立了CA-GA模型，以PTCN公司车间调度为例，根据设备故障情况和订单插单情况，进行了一次原始调度和两次再调度，将最终优化方案与实际生产计划进行对比，从而验证了该模型的可行性，并通过鲁棒指标评价了再调度的优越性.但目前关于多态性作业车间鲁棒调度的研究还不完整，在考虑不确定因素对调度的影响时只提及设备故障和插单情况，且设计目标函数时只考虑了三个子目标.今后的研究中，可考虑将更多的不确定因素加入模型，并加入其他目标进行进一步探讨.

参考文献：

[1] SATAPATHY G, SOUNDAR R T K, MOORE L M. World-class logistics: managing continuous change(DIAL)[J]. Expert Systems with Applications,2011,14(8)：409-424.

[2] 鞠全勇,朱剑英.多目标批量生产柔性作业车间优化调度[J].机械工程学报,2007,43(8)：148-154.

[3] 刘爱军,杨育,刑青松,等.柔性作业车间多目标动态调度[J].计算机集成制造系统,2011,17(12)：112-119.

[4] NASR A H, ELMEKKAWY T Y. Robust and stable flexible job shop scheduling with random machine breakdowns using a hybrid genetic algorithm[J]. Production Economics,2011,132:279-291.

[5] WEI Lei, LIN Xin, WANG Meng, et al. A cellular automaton model for the solidification of a pure substance[J]. Applied Physics A: Materials Science & Processing,2011,101:123-133.

[6] HAN Y S, KO S K. Analysis of a cellular automaton model for car traffic with a junction[J]. Theoretical Computer Science,2012,450:54-67.

[7] 陈锦昌,詹伟杰,姜立军.基于2.5维元胞机的人群疏散模型[J].工程图学学报,2009(5):170-176.

[8] 陈勇,阮幸聪,王亚良.基于元胞机的大型机械构件生产车间柔性调度求解[J].浙江工业大学学报，2011,39(4)：433-439.

[9] LEON V J, WU S D, STORER R H. Robustness measures and robust scheduling for job shops [J]. IIE Transactions,1993,26(5):32-43.