等三相感应电机单相运行磁场定向控制策略研究

杜友武，方明星，王 瑞

(1.安徽师范大学 物理与电子信息学院，安徽 芜湖 241000；2.华中科技大学 控制科学与工程系院，湖北 武汉 430074)

等三相感应电机单相运行磁场定向控制策略研究

杜友武1，方明星1，王 瑞2

(1.安徽师范大学 物理与电子信息学院，安徽 芜湖 241000；2.华中科技大学 控制科学与工程系院，湖北 武汉 430074)

本文研究三相感应电机出现故障导致缺相运行时，基于磁场定向控制理论控制电机继续可靠稳定运行，确保不出现连锁性事故.首先基于三相感应电机单相运行等效电路分析了电机运行的特点，通过构建单相供电下电机正负序电流，推导出电机单相运行下，磁场定向控制的电磁转矩显性表达式，得出相应的控制框图.MATLAB仿真结果表明，当三相电机某相出现开路导致缺相运行情形下，采用磁场定向控制策略，电机仍然能够可靠稳定运行，电机运行速度越高，其空载和带载两种情形下的稳定性越好，从而验证了本文控制方法的有效性.

缺相；磁场定向控制；三相电机；Matlab仿真

随着电机控制理论的发展，矢量控制已经成为电机控制领域的标准技术.矢量控制能够让交流电机可以像他励直流电机那样进行解耦控制，使交流电机的控制性能得到大幅度的提高，文献也大都集中在三相电机的矢量控制研究[1-2].然而，一旦三相电机某相出现故障而使该相断开，将会导致连锁性故障，为了确保电机在缺相情况下继续可靠稳定运行，研究三相电机单相运行下的磁场定向矢量控制策略具有一定的现实意义.

研究表明三相电机单相运行情况下，其带负载能力远远低于三相，并且存在低频振荡转矩，不利于设备正常工作，通过引入开环矢量控制以及注入奇次谐波电流等方法改善三相电机缺相下的运行情况[3-4].本文首先给出了三相感应电机单相运行时的简化等效电路，并基于此分析电机单相运行的特点；然后通过构建正负序电流分量，推导出电机单相运行下，磁场定向控制的电磁转矩显性表达式，并得出了相应的控制框图；最后在Matlab平台上进行了仿真验证.

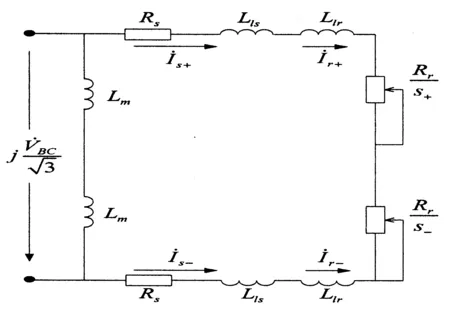
图1 感应电机单相运行简化等效电路

1 电机单相运行磁场定向控制策略

假设三相感应电机A相断开，则电机由线电压VBC供电，依据对称分量法图1给出了三相感应电机单相运行下的简化等效电路[5-8].其中：

Rs、Rr电机定转子电阻

Lm、Lls、Llr电机互感，定转子漏感

Is、Ir电机定转子电流

s转差率

+、- 正负序分量标志

由图1可以解出：

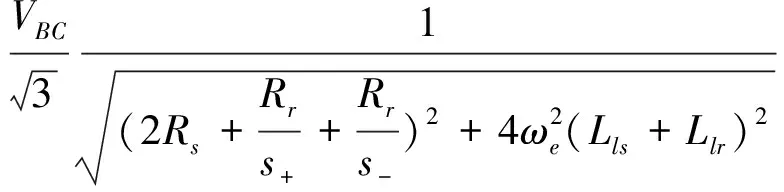
(1)

考虑到s-=2-s+，则有转矩

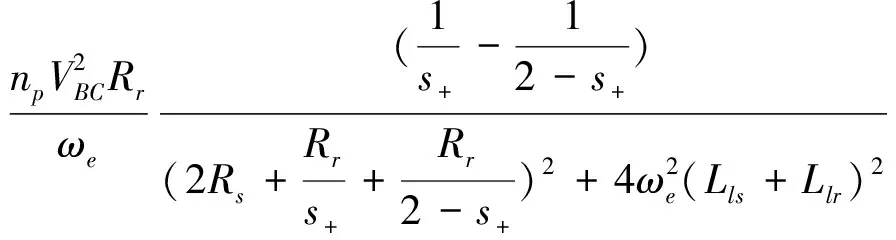
(2)

式(2)是感应电机单相运行时的机械特性方程式.从式中可以看出，当转差率一定时，电磁转矩与定子电压的平方成正比，这一点和三相对称运行时的结论是一样的.

当s+很小时，上式可以简化为

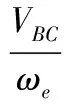
(3)

此时转矩近似与s+成正比.当s+等于1时，从式(2)可以看出转矩为零.也就是说，感应电机单相运行没有启动转矩.当电机借助外力转动起来后，观察图1可以知道，正向磁场阻抗Z+大于电机静止时的值，反向磁场阻抗Z-小于电机静止时的值.也就是说正向磁场反电动势大于反向磁场反电动势，或者说正向磁场增强反向磁场减弱.随着正序转差率的降低，正负序合成气隙磁场越接近于圆形[5].

从上述理论分析的基础上可知，三相感应电机恒压频比控制(V/f控制)同样可以适用于单相运行的情况，控制框图如图2所示.

图2 感应电机单相运行恒压频比控制结构框图

考虑到电机定子缺相工作在非对称状态，故在α-β坐标系下建立电机数学方程.假设A相断开，则iA=0，iB=-iC，

(4)

由isα=0可得缺相运行时定转子电压、磁链以及转矩方程如下：

电压方程：

(5)

磁链方程：

(6)

转矩方程：

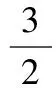
(7)

在单相供电下，定转子电流均为交流分量，从式(7)可以看出电流的乘积无法保证得到一个恒定的电磁转矩，当然，通过合适的控制方案可以调节得到所需的转矩平均值，这和前面用对称分量法分析得到的结论是一致的.

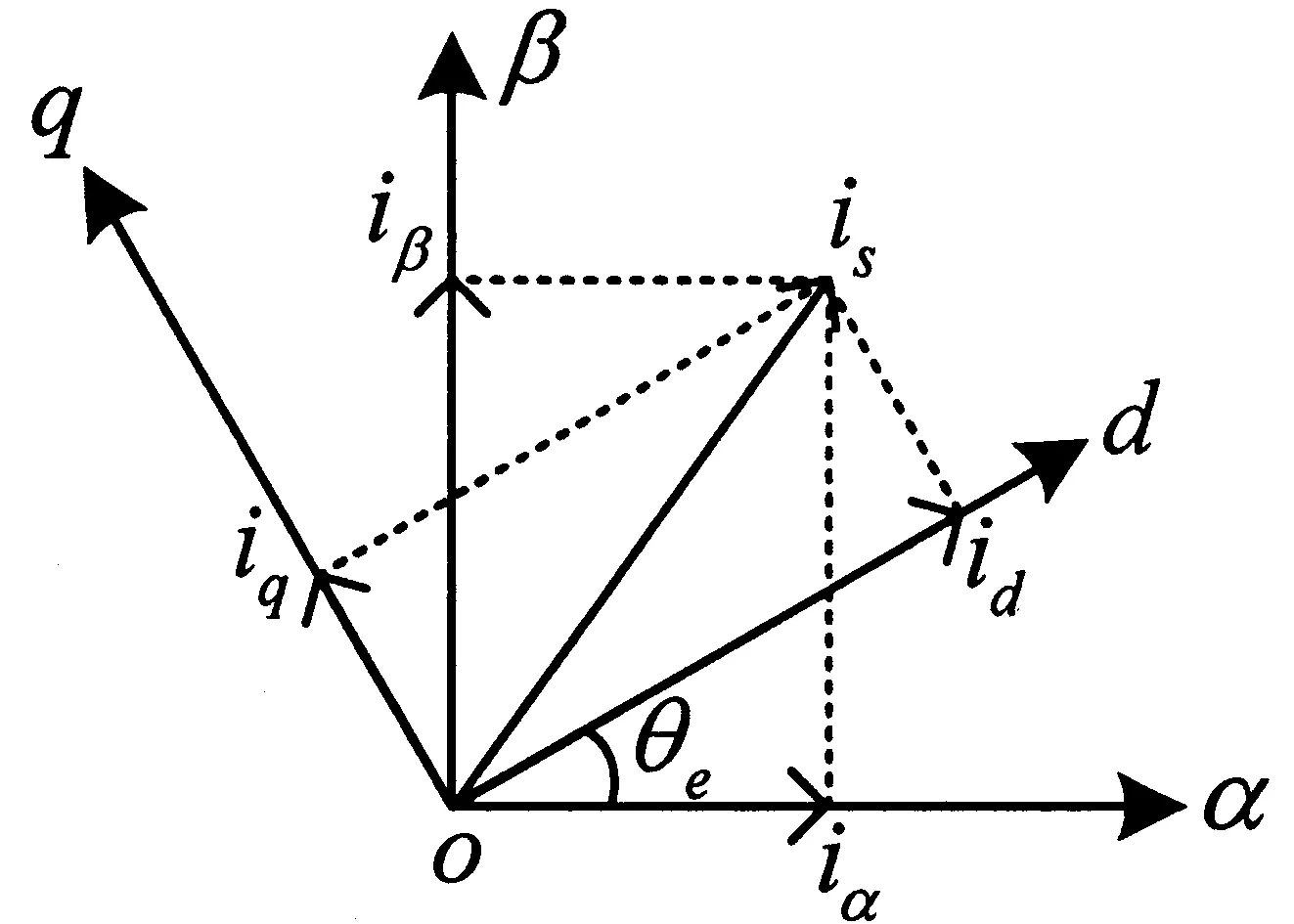
图3 两相静止坐标系到两相旋转坐标系转换示意图

根据对称分量法，单相供电下产生正序和负序转矩，单相电流无法同时控制这两个转矩.然而，如果能够控制正序转矩，同时估计出负序转矩，那么就可以通过控制正序转矩来抵消负序转矩，从而得到所需的平均转矩[9-10].为了分析问题的方便，这里首先给出两相静止坐标系(α-β)到两相旋转坐标系(d-q)变换，如图3所示.

建立两坐标系下变量转换关系如下：

(8)

该变换通常称为Park变换，其逆变换为：

(9)

d轴称为直轴，q轴称为交轴，θe为两坐标系间的夹角.在间接转子磁场定向矢量控制中，θe可由下式获得

(10)

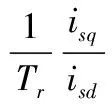
(11)

其中，ωr为转子电气角速度，ωsl为转差角速度，T为电机转子时间常数.

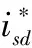
根据给定电流得到α-β坐标系下的给定正负序电流分量为：

(12)

(13)

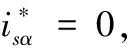
θe-=2ε-θe

(14)

(15)

由式(12)-(15)计算得

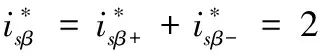
(16)

结合式(4)和(16)有

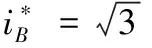
(17)

式(17)给出了单相供电相电流给定值，理想情况下实际相电流与该给定电流相等，利用Clarke和Park变换得d-q坐标系下的电流分量为：

(18)

从上式可以看出，实际电流的dq轴分量除含有给定分量外，还包含了两倍供电频率的交流分量，这正体现了单相供电的特点.

式(16)给出了定子电流β轴分量，利用式(7)计算转矩，还需要计算得到转子电流α轴分量irα.根据式(6)第三行有：

ψrα=Lrirα

(19)

同时，易知

ψrα=ψrcosθe=Lmimcosθe

(20)

其中，ψr为转子磁链幅值，im为励磁电流.结合式(19)和(20)有

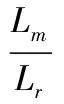
(21)

根据式(7)、(16)和(21)，得电磁转矩

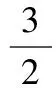
(22)

根据式(15)和(16)，注意到

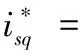
(23)

结合式(18)，则式(22)可以转化为

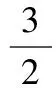
(24)

从上式可以看出，电磁转矩由电机参数，励磁电流以及定子电流q轴分量三者的乘积共同决定，这和正常运行时的结论是一致的.不同的是，这里im和isq均含有交流分量，导致转矩波动.在无转速环控制系统中，转矩给定需要根据和计算得到转矩平均值，而在带转速闭环控制系统中，这种计算可以省略，因为转速环会根据带载情况自动进行补偿[11].基于上述分析，得到整个单相闭环运行控制框图如图4所示.

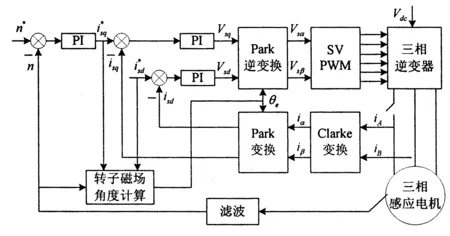
图4 感应电机单相闭环磁场定向运行控制框图

图中所示，系统包含两个控制环，外环为速度环，内环为电流环.外环速度误差通过PI调节器得到q轴电流给定，内环PI调节器的输入为交流量，输出为dq轴电压，经过Park逆变换转换到α-β坐标系，最后经过SVPWM调制得到控制逆变器所需的PWM开关信号.其中，坐标变换所需转子磁场角度θe由转子电气角速度和转差角速度之和的积分获得.对于转速波动比较大的场合，设置相应的低通滤波器，目的是为了得到转速平均值，继而得到q轴电流给定平均值.

上述控制方案和三相正常运行时的方案基本上是一致的.然而，有一点需要注意， 单相运行势必产生两倍供电频率的转矩脉动，虽然这种脉动不产生平均转矩，但会造成电机振动和噪声，特别是在小惯量系统中将导致严重的轴振动，疲劳，齿轮磨损甚至机械谐振.这种脉动在单相运行时是不可避免的，是由单相输入功率脉动特性本身所决定的.

2 仿真分析

为了验证上述分析的正确性，在MATLAB中搭建了三相感应电机单相运行仿真平台.电机额定电压1050V，额定电流129A，额定转速1800rpm，额定输出转矩1007Nm.考虑到电机单相运行没有启动转矩，故在仿真中待电机启动后再通过开关将A相断开.

图5和图6给出了100rpm和1000rpm两种单相开环空载运行工况下的转速以及相电流对比图.仿真在1.5s时刻切换到单相运行，从图中可以看出，低速下转速波动明显，理论上2倍频脉动周期为0.15s，这和图5所示很吻合.高速下转速波动幅值变小，相电流与低速时相比更接近正弦波.也就是说，随着转速的升高，空间正序磁场将会增强，负序磁场将会减弱.

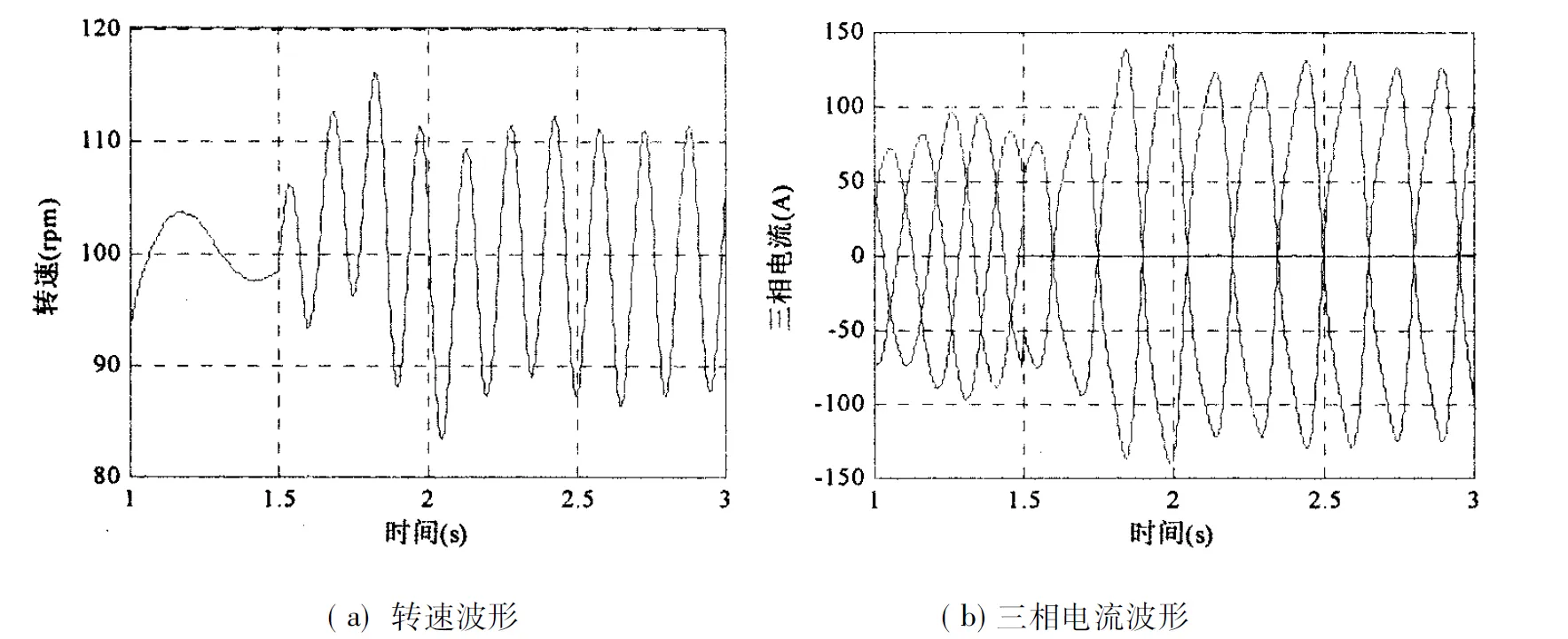
图5 单相开环100rpm时电机转速以及三相电流波形

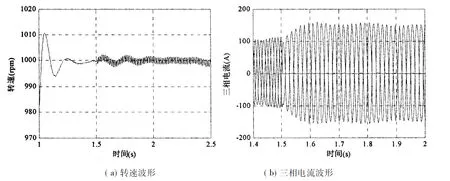
图6 单相开环1000rpm时电机转速以及三相电流波形

图7和图8给出了100rpm和1000rpm单相开环带载前后的转速波形.仿真在1.5s时刻切换到单相运行，2s时刻突加400Nm恒转矩负载.从图中明显可以看出，低速下突加负载后转速跌落，系统无法继续工作.高速下突加负载后，尽管存在一定的转速降，但仍然可以维持系统继续运行.这正验证了前面的分析，电机单相运行带载能力随着转速的升高而增强.

图7 单相开环100rpm带载前后转速

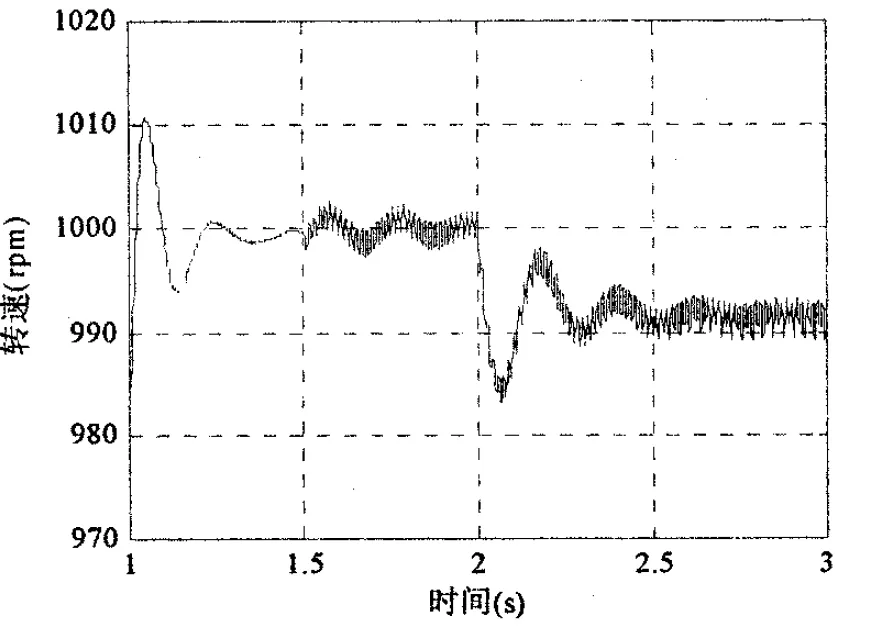
图8 单相开环1000rpm带载前后转速

图9和图10给出了600rpm单相闭环带载前后的转速以及轴电流波形.仿真在2.5s时刻切换到单相运行，3s时刻突加400Nm恒转矩负载.从图中可以看出，转速同样存在两倍供电频率的脉动，轴电流由直流分量和两倍供电频率的交流分量所组成.突加负载后，轴电流直流分量没有变化，轴电流直流分量自动调节到负载所需.这和前面的分析是一致的，验证了单相闭环运行的可行性.

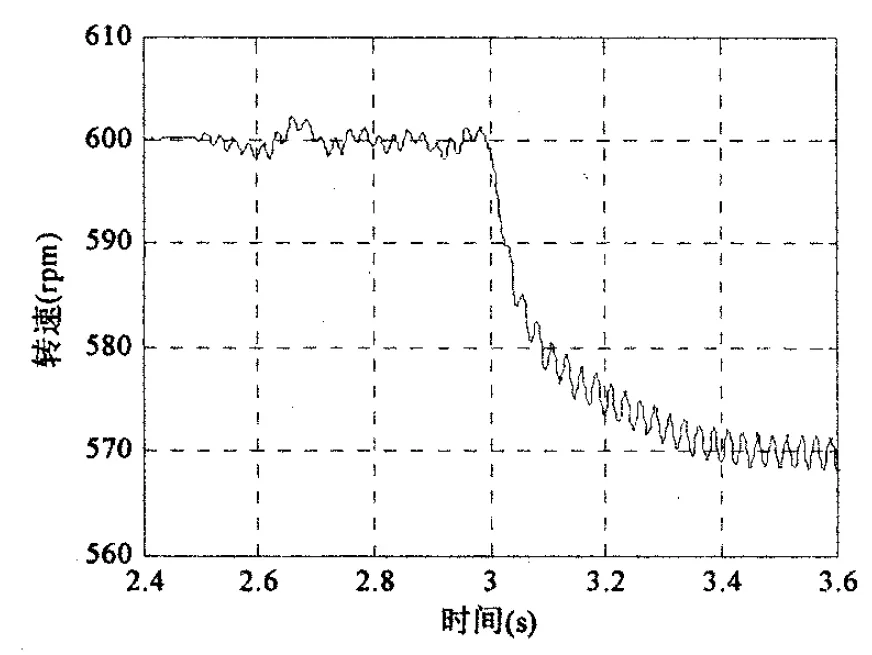
图9 单相闭环600rpm带载前后转速

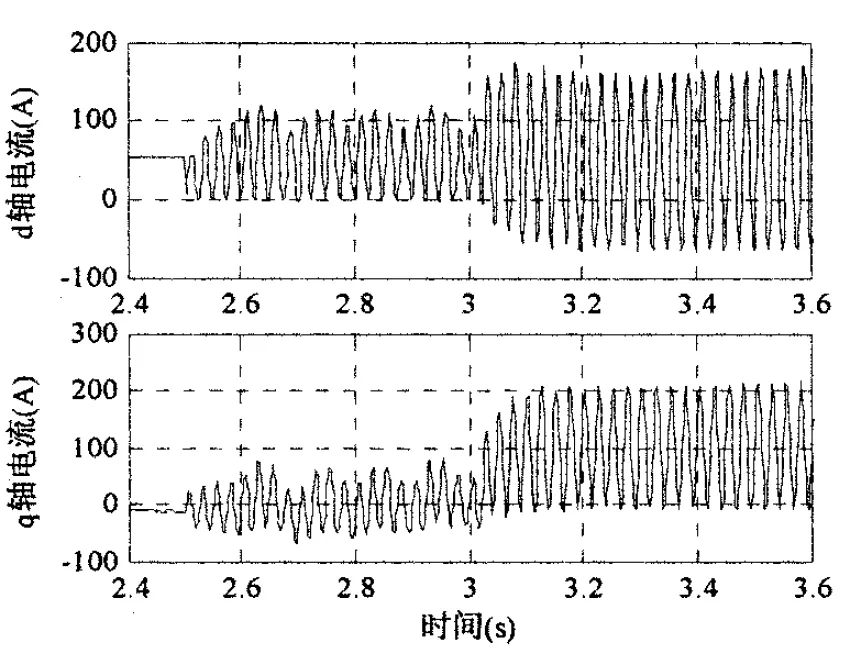
图10 单相闭环600rpm带载前后轴电流

3 结论

本文针对三相感应电机缺相运行下磁场定向控制进行了详细的理论分析.通过对电机单相运行下等效电路的求解，指出单相运行时传统的电压频率开环控制方案仍然是可行的.继而在同步旋转坐标系下推导了磁场定向闭环控制方案，与正常运行不同的是，闭环调节器的输入均为交流量，为了得到内环电流给定平均值，对于低转动惯量场合，需要设置转速低通滤波器，而对于机车牵引等转动惯量比较大的场合，滤波器的设置相对而言没那么重要.最后，对理论分析进行了仿真验证，得出了与分析一致的结果.

[1] 刘军华,王清灵,毕惠娟.基于DSP的三相空间矢量脉宽调制整流器研究[J].电力电子技术,2011,45(9):123-126.

[2] BIMAL K. Bose. Modern power electronics and AC drives[M]. Beijing: Mechanical Industrial Publishing House, 2005.

[3] Edward Randolph Collins. Torque and slip behavior of single-phase induction motors driven from variable-frequency supplies[J]. IEEE Transactions on Industry Application, 1992,28(3):710-715.

[4] Debaprasad Kastha, Bimal K Bose. Fault mode single-phase operation of a variable frequency induction motor drive and improvement of pulsating torque characteristics[J]. IEEE Transactions on Industrial Electronics, 1994,41(4):426-433.

[5] 王伟，封立泽，刘占民.管道检测机器人的设计和系统分析[J].安徽师范大学学报:自然科学版,2013，36(6)：546-549.

[6] 方进，申敏.轨道交通用高温超导直线感应电机的设计与测试[J].安徽师范大学学报:自然科学版，2013，36(4)：307-313.

[7] PAUL C. Krause, Oleg Wasynczuk, Scott D. Sudhoff. Analysis of electric machinery and drive systems[M]. New York: Wiley Interscience, 2002.

[8] William H. Kersting. Causes and effects of single-phasing induction motors[J]. IEEE Transactions on Industry Applications, 2005,41(6):1499-1505.

[9] Amr Saleh, Mario Pacas, Adel Shaltout. Fault tolerant field oriented control of the induction motor for loss of one inverter phase[C]. Proceedings of 32nd Annual Conference of the IEEE Industrial Electronics Society, 2006,817-822.

[10] Amr Saleh, Adel Shaltout, Mario Pacas. Fault tolerant field oriented control of induction motor for loss of one inverter phase with re-starting capability[C]. IEEE International Symposium on Industrial Electronics, 2007,(1)：1340-1345.

[11] 刘忠举,梁宝明,陈嘉福.基于改进型积分器的矢量控制系统的研究[J].电力电子技术,2010,44(2):62-64.

AnalysisofSinglePhaseFieldOrientedControlStrategyofInductionMotor

DU You-wu1, FANG Ming-xing1, WANG Rui2

(1.College of Physics and Electronic Information, Anhui Normal University, Wuhu 241000, China; 2. Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China.)

To ensure there will be no cascading failure of induction motor in default of one stator phase, the motor control strategy is studied under this condition based on field oriented theory. The operational characteristic is first analyzed according to the equivalent circuit of motor in default of one stator phase. By constructing the positive and negative currents under single phase power supply, the motor torque formulation is then derived and the field oriented control schematic diagram is presented. The simulink results in MATLAB show that the motor with one stator phase opened can still be operated well using rotor field oriented control. It is also concluded that the higher motor speed is, the more stable motor will be with or without load, which validates the availability of the method.

phase default; field oriented control; three phase motor; Matlab simulations

2013-10-15

国家自然科学基金项目(21173002)；安徽省自然科学基金项目(11040606M118).

杜友武(1984-)，男，安徽巢湖人，硕士，助教，主要研究方向为电力电子与机电控制.

杜友武，方明星，王瑞.等三相感应电机单相运行磁场定向控制策略研究[J].安徽师范大学学报：自然科学版，2014，37(1)：33-38.

TM346

A

1001-2443(2014)01-0033-06