基于滑模方法的挠性航天器姿态稳定控制*

史小平，李 隆，杨 婧，毕显婷，刘海龙

哈尔滨工业大学航天学院控制与仿真中心，哈尔滨 150080

1．Introduction

Spacecraft attitude control system is an important part in the whole spacecraft control system，considerable amount of work has been dedicated in recent years to the problems of spacecraft attitude control．The paper［1］address the attitude stabilization problem for a spacecraft is through the combination of optimal control and sliding mode variable structure control method．The proposed controller is also robust to external disturbances．For an under actuated spacecraft with two control actuators［2］，designs an attitude controller based on hierarchical sliding-mode control algorithm．The paper［3］investigates a quaternion-based finite time attitude synchronization and stabilization problem for satellite formation flying．A nonlinear control law based on a finite time control technique is developed such that the attitude of the rigid spacecraft will coordinate and converge to the attitude of the leader，while the angular velocity will converge to zero in finite time．In paper［4］，the problem of inertial pointing for a spacecraft with magnetic actuators is addressed and an almost global solution to the problem is obtained by means of static attitude and rate feedback．A local solution based on dynamic attitude feedback is also presented．Simulation results demonstrate the practical applicability of the proposed approach．The problem of attitude stabilization for a spacecraft system which is nonlinear in dynamics with inertia uncertainty and external disturbance is investigated in paper［5］，an adaptive law is applied to estimate the disturbances，where a sliding mode controller is designed to force the state variables of the closed-loop system to converge to the origin．Then，the spacecraft system subjected to control constraints is further considered，and another adaptive sliding mode control law is designed to achieve the attitude stabilization．Sliding mode control algorithm is used in rigid spacecraft attitude control system widely［6-9］．

Papers mentioned above only considered the stability of spacecraft attitude control system，however，the effect of orbit maneuver is not mentioned．In this paper，we take the problem of flexible spacecraft attitude stabilization at the presence of both the external disturbance torque and orbit maneuver．A flexible spacecraft attitude controller based on sliding mode algorithm is proposed．In contrast to common spacecraft attitude controller design，the sliding mode controller designed in this paper only need the information of attitude angular without the knowledge of the attitude angular velocity．Resources used in the attitude control system are greatly saved．

2．Description of mathematical model of flexible spacecraft orbit and attitude system

2．1．Dynamic equations

During orbit maneuvering，the dynamics model of flexible spacecraft with orbit control force established by Lagrange equations can be expressed as

Where m∈R is the total mass of the flexible spacecraft，V0=［V0xV0yV0z］T∈R3is the translational speed of the spacecraft，ω =［ωxωyωz］T∈R3is the attitude angular velocity expresses in the spacecraft’s body-fixed reference frame relative to the inertial coordinate system，η =［ηxηyηz］T∈R3is the model shape，F∈R3is the orbit control force during spacecraft orbit maneuvering;It∈R3×3is the flexible spacecraft’s symmetric moment of inertia matrix;L∈R3×3is the orientation matrix of reaction wheels，u∈R3is the control torque generated by three orthogonal reaction wheels，d=［dxdydz］T∈R3is the external disturbance，CVis the coupling coefficient matrix between flexible vibration motion and translational motion，Ca∈R3×3is the coupling coefficient matrix between flexible vibration motion and rotational movement，Λ =diag (ω2n1，ω2n2，ω2n3)∈R3×3is the stiffness matrix，D=diag(2ξ1ωn1，2ξ2ωn2，2ξ3ωn3)is the flexible modal damping matrix．Γ is the coupling coefficient matrix between flexible vibration motion and active vibration suppression controller．uηis the input vector of active vibration control．Here we define

where x=［x1x2x3］T∈R3．

2．2．Kinematic equations

The angular velocity vector of the flexible spacecraft described by Euler angles can be expressed as

Whereωbois the angular velocity vector of body-fixed reference frame relative to the orbit coordinate system，ωoiis the angular velocity vector of orbit reference frame relative to inertial system，Θ=［φ θψ］Tare the attitude angles described by Euler angles，ω0is the orbit angular velocity，R(Θ)and Z(Θ)can be expressed as

When the spacecraft is under the condition of small Euler angle motion，the angular velocity vector can be simplified as

In this case，the vector of gravity gradient torque on the spacecraft body axis can be expressed as

3．Main results

Here we define the auxiliary variableε=［η˙η V0］T，then equation(1)～(4)can be rewritten as

where

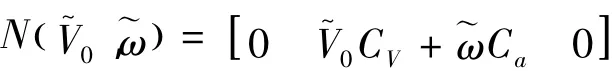
From Equation(8)，we obtain

Substituting Equation (9)into Equation(7)obtains

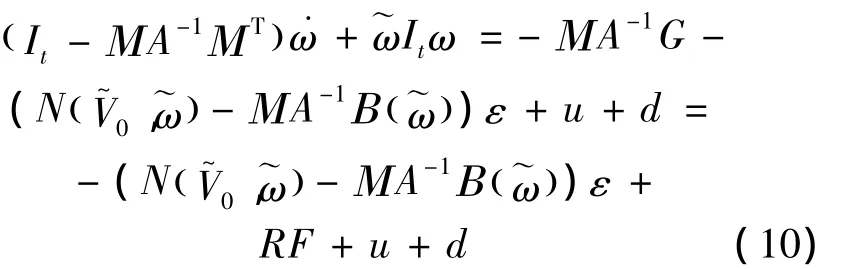
Here we ignore the inertia product of spacecraft，and assume It=diag(IxIyIz)．Substitute Equation(5)into equation with the considering of gravity gradient torque，then the flexible spacecraft dynamics described by Euler angles can be given as

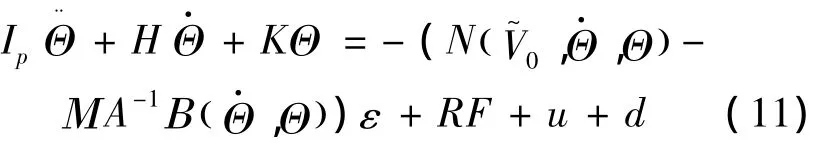
where

The whole unknown disturbance of the attitude control system Tdis defined as

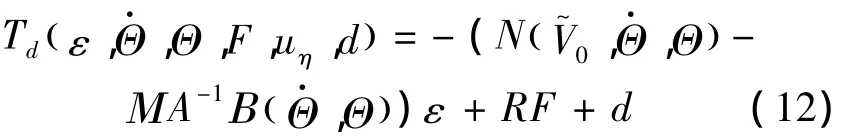
Here，we choose the sliding surface s as

where α ＞0 is a positive constant．

Assumption 1 The disturbance Tdis bounded，but the value of the bounds is unknown．

And we have the following definition

Where，ρis the boundary of Td，and it is an unknown positive value;^ρis the estimate value ofρ．Then the following theorem can be obtained．

Theorem 1 Considering the nonlinear flexible spacecraft attitude control model described by equation，if assumption1 is available，by selecting suitable control coefficientsγandβ，and choosing the attitude control laws in Equations(17)～(18)，then the closed-loop system is global asymptotic stability under disturbances and satisfies

whereβ ＞ ( α Ip-H )max．

Proof Considering the following Lyapunov function

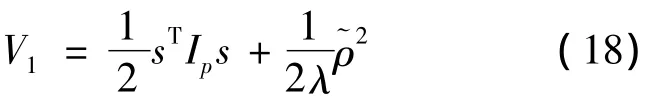
The time derivative can be expressed as

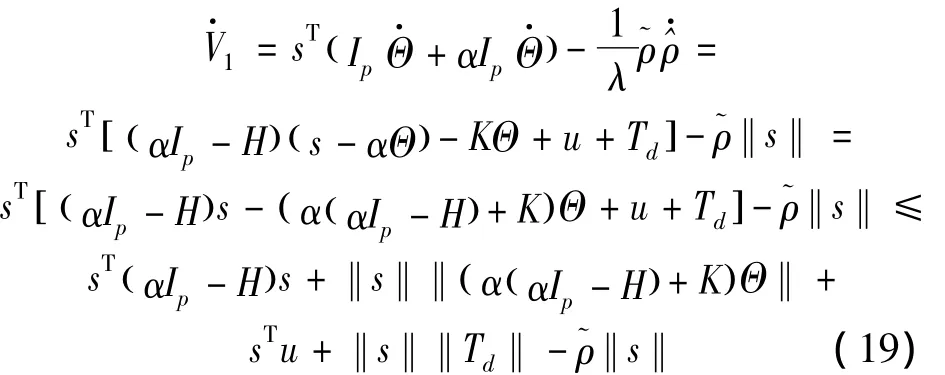
Form Equation(17)，we can obtain

Substituting Equation(22)into Equation(21)gives

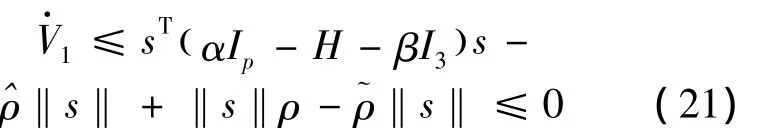
4．Simulation results

In order to demonstrate the effectiveness of the proposed approach，the application of the sliding mode control approach in this paper to the flexible spacecraft attitude control during orbit maneuver is presented using MATLAB software．The simulation parameter settings are as follows．

1)The initial value of attitude angular:

2)The initial value of attitude angular velocity:

3)Symmetric inertia matrix of the whole structure:

4)External disturbance:

Figure 1～Figure 3 are simulation results:

Figure 1．Time history of the attitude angular

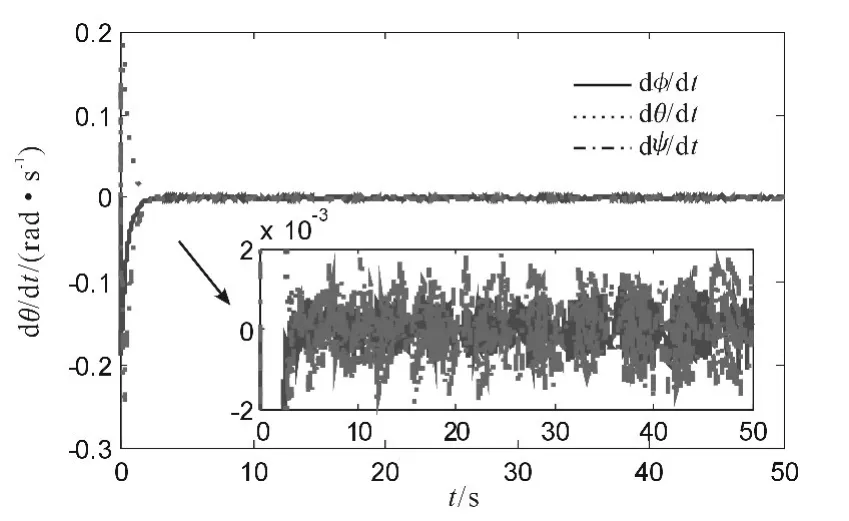
Figure 2．Time history of the angular velocity

Figure 3．Sliding mode surface

As can be seen from Figure 1～Figure 3，under the action of the proposed sliding mode attitude controller of flexible spacecraft，the closed loop system is asymptotically stable under unknown external disturbances and orbit control force．The simulation results exhibit excellent robust performance and demonstrate the validity and the correctness of the designed proposal．

5．Conclusion

This paper considers the attitude stabilization of flexible spacecraft with appendage vibration caused by external disturbance torque and orbit maneuver．The attitude controller is designed based on sliding mode algorithm．In contrast to other literature，the sliding mode controller designed in this paper only need attitude angular information with the knowledge of attitude angular velocity．The simulation results demonstrate that the spacecraft attitude system maintains stable and has the property of robust in the existence of external disturbance and orbital control force．

［1］ Chuanjiang Li，Yibo Wang，Liang Xu，et al．Spacecraft Attitude Stabilization Using Optimal Sliding Mode Control［J］．3rd International Symposium on Systems and Control in Aeronautics and Astronautics，2010(6):1085-1089．

［2］ WANG Dong-xia，JIAYing-hong，JIN Lei，et al．Hierarchical Sliding-Mode Control for Attitude Stabilization of an Under actuated Spacecraft［J］．Journal of Astronautics，2013，34(1):17-24．

［3］ Jiakang Zhou，Qinglei Hu．Decentralized Finite Time Attitude Synchronization Control of Satellite Formation Flying［J］．Journal of Guidance，Control and Dynamics，2013，36(1):185-195．

［4］ Lovera M，Astol A．Spacecraft attitude control using magnetic actuators［J］．Automatica，2004，40:1405-1414．

［5］ Zheng Zhu，Yuanqing Xia，Mengyin Fu．Adaptive sliding mode control for attitude stabilization with actuator saturation［J］．IEEE Transactions on INDUSTRIAL ELECTRONICS，2011，58(10):4898-4907．

［6］ VADALI SR．Variable-structrure Control of Spacecraft Large-angle Maneuvers［J］．Journal of Guidance，Control and Dynamics，1986，9(2):235-239．

［7］ LOSC，CHEN Y P．Smooth Sliding-mode Control for Spacecraft Attitude Tracking Maneuvers［J］．Journal of Guidance，Control and Dynamics， 1995， 18(6):1345-1349．

［8］ CRASSIDIS J L，MARKLEY F L．Sliding Mode Control Using Modified Rodrigues Parameters［J］．Journal of Guidance，Control and Dynamics，1996，19(6):1381-1383．

［9］ Feng Lu，Gong Cheng，He Changand．Error Quaternionbased Spacecraft Attitude Tracking System with Sliding Mode Control［J］．Journal of Astronautics，2000，21(1):17-22．