析解法 赏亮点 促反思——由—道高考题引发的复习教学反思

安徽省涡阳县第四中学 (邮编：233600)

安徽省涡阳县大理中学 侯立田 (邮编：233600)

每年的高考结束后，我们都会从全国各省市的数学试卷中发现不少优秀的试题，这些试题凝聚着命题者的智慧，同时也给我们以教学的启迪.笔者近来研究今年的试题时，发现高考数学安徽卷理科第19题是一道挺不错的题目，既符合教学的实际，又符合高考命题的理念，值得细细品味.

题目已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0)，过原点 O 的两条直线l1和l2，l1与E1、E2分别交于A1、A2两点，l2与E1、E2分别交于B1、B2两点.

(Ⅰ)证明：A1B1∥A2B2；

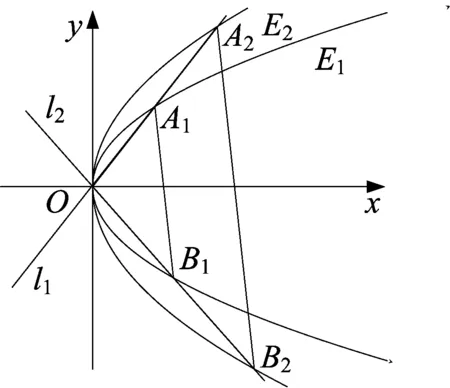
图1

1 析解法

(Ⅰ)法1设直线l1的方程为y=k1x，与抛物线E1的方程联立，得

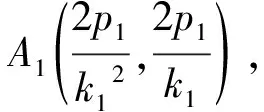
法2同法1，知A1、B1、A2、B2的坐标.

(Ⅱ)由(Ⅰ)知A1B1∥A2B2，C1B1∥C2B2，可得△A1B1C1与△A2B2C2相似,

法1|A1B1|

|A2B2|

法2由(Ⅰ)的法2知，

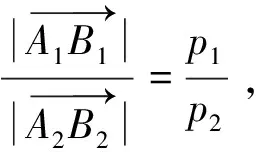
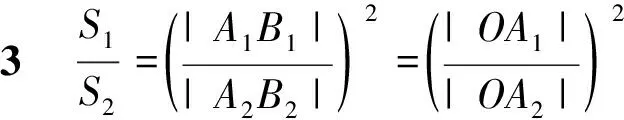
2 赏亮点

2.1 回归基础

本题从题目的文字和符号较多来看，好似一道难题，其实从解法来看，可以说还是注重基础知识的考查.两小问的法1涉及到直线与圆锥曲线的交点、两直线的位置关系和两点间的距离等都是平面解析几何的基础知识，也不用什么高技巧.

2.2 解法灵活

本题入口宽，解法较为灵活.第(Ⅰ)问既可以用斜率解，也可以用向量解；第(Ⅱ)问的三种解法分别运用了两点间的距离、向量知识和比例转换去解，可谓是仁者见仁，智者见智，各显神通.

2.3 贴近教学

本题的设计关注了高中教学的实际和初、高中教材的衔接，由于韦达定理在初中教材中作为选学内容，不作中考考试要求，致使各地在实际教学的要求不同，因而不能作为高考的统一要求，本题很好地回避了解析几何中对韦达定理的运用.

2.4 少算多思

“少一些计算，多一些思考”一直是高考的命题理念之一，从本题的解答来看，步骤较为简洁，没有了繁冗的计算，第(Ⅱ)问法1由于运用了两点间的距离公式，看似繁琐，实则简单，因为不需太多的化简，可以说本题重在考查学生的思维品质和数学修养，是道好题！

2.5 图形美观

本题不但闪烁着理性的光辉，而且具有“形”之美观.我们先看两条共顶点的抛物线，好似开放的花朵，给人以美的享受；再者，如果我们把△A1B1C1与△A2B2C2作出，我们还可以欣赏到两条抛物线与△A1B1C1和△A2B2C2构成得整个图形的和谐之美、奇妙之美！

3 促反思

“一滴水可以折射阳光的七彩”，一道考题可以反映我们的教学.从2014年安徽卷的这道题目的学生做题情况来看，并不乐观，有的学生空白没做，有的学生写了寥寥几笔，只有少数学生能进行到底.为什么这样一道计算并不繁琐的题目却出现如此情况呢？值得反思一下我们的教学.笔者认为，就本题而言，我们教学中有以下几个方面的缺失.

3.1 重视课本不够

课本是数学知识的载体，是师生教与学的重要依据，是许多专家们精心组织编写的，包括例题习题都是经过反复推敲的，凝聚着他们的智慧和心血；课本也是高考命题的重要来源之一，有的考题直接或间接取材于课本，陕西的高考曾考余弦定理的证明，2014年安徽理科就考了贝努利不等式的证明与利用，这些考题都直接取自课本.但是在全国各地的高三复习迎考中，摒弃课本的做法还普遍存在.其实数学课本能给我们提供许多高三复习教学的素材，如果我们认真去研究课本，对一些问题进行拓展、延伸和重组，就能发现许多精彩的问题.就本题来说，我们就能在课本中找到该题的影子，在《数学》(选修2-2)课本第89页习题A组第3题:求直线3x-2y=0和椭圆4x2+y2=25的交点.课本习题是求过原点的直线与椭圆的交点,而考题是需求过原点的直线与抛物线的交点,可见两题十分接近.

3.2 思维训练不足

本题从解法来看,重思维而轻计算,学生解答不好,正反映了我们平时的教学对思维训练力度不足.我们平时教学可以说有以下几种常见现象:⑴教师讲的时间多而学生思考时间少,学生没有足够的时间思考,影响了学生的良好思维品质的形成;⑵题目讲题多而拓展延伸少,就题论题,学生思维的广度、深度和灵敏度得不到很好地训练;⑶常规问题讲得多而创新问题涉及少,致使学生对常规问题得心应手,一旦碰到新颖的问题心里慌张,束手无策.就拿本题来说，我们平时在课本和资料上见到的多是直线和单个抛物线(或双曲线、椭圆)，此题给了两条抛物线，题目比较新颖，不少同学见了头脑混乱，找不到解决问题的突破口，反映了同学思维能力的不足.其实我们只需选择一条直线和其中一条抛物线作为突破口，就可以轻松把问题解决掉.此题告诫我们在平时的教学中要高度重视学生的思维训练，首先在时间上要给学生思维的空间，在内容上要引导学生向思维的广度和深度方面发展，同时关注创新思维的培养.

3.3 向量意识不强

向量是高中课程改革的新增内容，由于向量具有“数”与“形”两方面的特征，因而有着广泛的应用，在立体几何和解析几何中如直线的平行与垂直、线段的长度、角的大小等问题都可以用向量来解决，充分发挥向量的工具作用.笔者曾对今年参加高考的考生作了调查，用向量解决的少之又少，说明考生运用向量解题的意识不强.从实际教学来看，我们一线教师注重立体几何中利用向量的教学较多，而解析几何中利用向量的教学较少，笔者认为这是在此考题中学生很少有利用向量解题的主要原因.

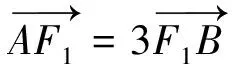
3.4 平几知识薄弱

第(Ⅱ)问采用平几知识进行比例转换，此法比较简洁，但多数考生没有想到，而这正反映了考生平面几何知识薄弱.笔者多年教学发现，在高三模拟和高考卷中只要涉及到与平面几何知识的结合，学生很容易失分.造成这种情况的原因主要有两种：其一是平面几何是初中时期学过的，高一高二用得少，造成遗忘；其二是平时教学中缺乏这方面的专门训练，以致运用平面几何知识的意识不强.现在有些省份选学《平面几何选讲》，笔者认为这是不错的选择，恰好可以弥补这方面的不足.在实际的教学中，我们应利用几个课时复习一下平面几何知识的几个重点，诸如三角形全等与相似、平行线与比例式、圆中的切线与垂径定理、圆与圆的关系等，并进行适量的训练,以此增强平面几何知识的运用意识.

4 结束语

高考试题是专家们精心命制的，是他们智慧的结晶.如果我们潜心研究高考试题，不仅能欣赏到数学的理性之光，还能够发现我们教学的缺失，益处多多，何乐而不为呢？

1 严士健，王尚志. 普通高中课程标准教科书(选修2-2)[M].北京：北京师范大学出版社.2008第3版

2 严士健，王尚志. 普通高中课程标准教科书(选修4-5)[M].北京：北京师范大学出版社.2008第3版