低精度INS/GPS组合导航大方位失准角初始对准方案

吴松羽,王可东

(北京航空航天大学宇航学院,北京 100191)

0 引 言

初始对准是惯性导航的关键技术之一,也是卫星/惯性组合导航系统的重要环节,一般分为粗对准和精对准两个阶段。传统的粗对准就是用解析方法将姿态失准角快速收敛到一个较小的范围内,为精对准阶段做准备。但在应用低精度微惯性测量单元(MEMS-IMU)的初始对准中,由于陀螺仪的误差较大,无法通过传统的解析自对准将方位失准角收敛到小角度。就造成了大方位失准角问题,导致系统方程的非线性。为了解决这个问题,一般有两种方法:一种是用非线性滤波方法替代线性卡尔曼滤波,进行非线性初始对准;另一种是建立新的线性系统方程,实现线性初始对准[1-4]。第二种方法的实时性好,更适合于车载组合导航系统应用。本文以文献[4]提出的一种方案为参考,用方位失准角的两个三角函数代替方位失准角作为状态量,建立新的线性系统误差方程,进行了可观测度分析,最后，在应用低精度MEMS-IMU和单天线GPS的组合导航车载试验中进行了验证,结果表明：在GPS和IMU精度均较低的条件下,初始对准方案仍具有很好的对准精度和对准速度,证明了方案的可行性。

1 初始对准系统方程

用方位角φ的三角函数sinφ和(cosφ-1)作为状态量,以ψ角误差模型法建立新的线性系统方程。本方案中地理坐标系取东北天(ENU),方位角正方向取北偏东为正。

1.1 粗对准系统方程

大方位失准角条件下,初始时水平失准角为小角量,方位失准角为大角量,由图1可以得到姿态矩阵为

图1 计算坐标系c与当地水平坐标系p’之间的关系

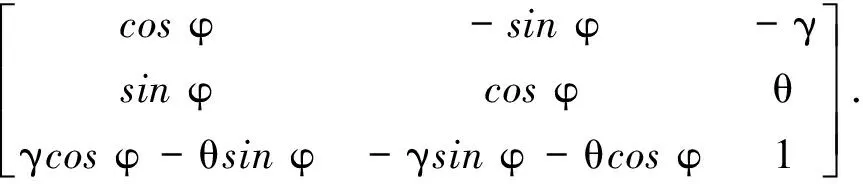
(1)

根据文献[5],在计算坐标系c中的惯导误差方程为

=fp-fc+δfp.

(2)

(3)

传统的姿态误差方程的表达式为[6]

(4)

方位失准角的两个三角函数sinφ和cosφ-1的误差方程显然为非线性。但初始时两个量变化很缓慢,即变化率很小,因此可以近似有

(5)

将姿态矩阵式(1)带入式(4)中,并与式(5)综合,得到姿态误差方程为

(6)

位置误差方程不包含非线性部分,因此与通用的方程相同[6]

(7)

1.2 精对准系统方程

在粗对准的姿态误差方程推导过程中,两个状态量sinφ和cosφ-1的模型存在较大误差,当方位角减小到一定值后,可以得到更加精确的模型。

根据式(4)可以推得

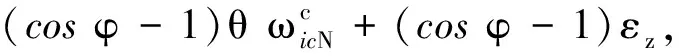
(8)

式中,θ、γ、εz均是小量,cosφ-1也是随着方位失准角的减小而趋于零的小量,当方位失准角减小到10°左右时,cosφ-1的值能减小到0.01左右。因此cosφ-1与θ、γ、εz的乘积为高阶小量,消去高阶小量近似得到

(9)

对于状态量cosφ-1,由余弦函数的特性可知,其模型仍与粗对准时相同。所以精对准姿态误差方程为

(10)

精对准的速度和位置误差方程同粗对准系统方程相同。

2 系统方程的可观测度分析

为了研究初始对准中各状态量的收敛情况与载体运动的关系,作为车载试验的参考,需要对系统方程进行可观测性分析。进行可观测性分析一般包括两部分:一是确定系统状态量是否完全可观测;二是确定系统及其状态量的可观测度。根据分段线性定常系统(PWCS)可观测性分析方法[7]进行分析,发现初始对准的系统方程的状态量完全可观测,因此，重点在于系统可观测度的分析。

对同一系统而言,系统状态量的可观测度越大,则在其他条件相同的情况下,滤波效果越好,即估计精度越高,收敛速度越快。最常用的可观测度分析方法是基于系统可观测矩阵奇异值分解法,即通过每个奇异值对应的初始状态量的大小,确定不同状态所对应的奇异值,从而定义系统各个状态的可观测度。本文选用一种省略观测量的改进奇异值分解法[8],通过分析奇异值的右奇异向量判断系统状态在不同时刻对应的奇异值,简化了分析步骤,同时也避免了奇异值标准的定义。

通过改进奇异值分解法对系统进行可观测度分析,选取不同的运动形式,观察系统各个状态量对应的可观测度的大小及其变化趋势,以便分析何种运动形式有利于状态量可观测度的提高。由于系统观测量为GPS与惯导解算的位置差和速度差,系统状态量中的位置误差和速度误差直接可观测,因此，重点分析与姿态失准角相关的系统状态量。经过分析研究发现,加速运动与圆周运动最有利于状态量可观测度的提高,匀速运动和静止状态不利于可观测度的提高。如图2所示,加速度的改变会使方位失准角相关状态量的可观测度有很大提高,说明运动形式的多变性有利系统状态量的观测。经过研究分析,最终得出初始对准的最佳运动轨迹为八字形轨迹。

图2 sin φ和cos φ-1的可观测度的变化

3 车载试验结果及分析

组合导航车载试验的硬件由精度较低的单天线GPS、MEMS-IMU、计算机组成。GPS的精度为5 m和0.5 m/s,IMU使用的是型号为ADIS16375的MEMS-IMU,其相关参数如表1所示。

表1 ADIS16375的相关参数

车载试验之前对IMU进行标定补偿,尽可能减小误差。车载试验的运动形式分为两部分:2 min的静止和5 min左右的八字运动。第一部分静止状态,是为了进行水平失准角的解析对准,得到水平失准角的初始值。第二部分八字运动状态,则应用本文中的初始对准方案进行车载试验,这部分运动的GPS测量轨迹如图3所示。

图3 八字运动的GPS测量轨迹

经过初始对准后,得到姿态失准角的估计如图4、图5所示。

图4示出的是水平失准角的估计结果,水平失准角经过静止状态下的解析粗对准收敛到较小的角度,在初始对准中的估计速度较快,在2 min左右就能收敛到4角分。图5示出的是方位失准角的估计结果,虽然对准初始阶段方位失准角较大,但方案中的卡尔曼滤波粗对准能够很快的将大方位失准角收敛,所以方位失准角在2 min左右就能收敛到10角分以内,并且收敛效果随着时间的增加而变得更好,在接近5 min时方位失准角估计收敛到了5角分。

图4 水平失准角估计

图5 方位失准角估计

同文献[4]中的高精度差分GPS相比,本方案使用的单天线GPS更简单,成本更低,适用范围更广。虽然车载试验中的IMU和GPS的测量精度均比文献[4]中的低,但对准结果中的对准时间和对准精度与文献[4]中的基本相同,证明了本方案对初始对准快速性和对准精度的提高。同时也说明了本对准方案在低精度组合导航中的适用性,其适用范围更加广泛。

4 结束语

本文针对车载低精度INS/GPS组合导航动基座初始对准的大方位失准角问题,通过变换状态量得到线性系统误差方程,建立了新的初始对准方案。在低精度的组合导航车载试验中,初始对准的结果具有很好的对准精度和对准速度,证明了本方案在低精度车载组合导航中的适用性。

[1]KELLEY R T,KATZ I N,BEDOYA C A. Design,development and evaluation of an adacoded INS/GPS open loop Kalman filter[C]//IEEE Conference on Aerospace and Electronics,Dayton,OH,USA,21-25 May,1990: 382-388.

[2]PHAM T M. Kalman filter mechanization for INS airstart[C]//IEEE:AIAA 10th Digital Avionics Systems Conference,Los Angeles,CA,USA,14-17 October,1991: 516-525.

[3]ROGERS R M. IMU in-motion alignment without benefit of attitude initialization[J]. Navigation: Journal of the Institute of Navigation. 1997,44(3)：301-311.

[4]HAN Songhai,WANG Jinling. A novel initial alignment scheme for low-cost INS aided by GPS for land vehicle applications[J]. The Journal of Navigation,2010,63(4),663-680.

[5]BENSON D O.A Comparison of two approaches to pure-inertial and Doppler-inertial error analysis [J]. IEEE Transactions on AES. 1975,11(4):447-455.

[6]WEINRED A,BAR-ITZHACK I Y. The psi-angle error equation in strapdown inertial navigation sytems[J]. IEEE Transactions on AES. 1978,14(3): 539-542.

[7]万德钧,房建成. 惯性导航系统初始对准[M].南京:东南大学出版社,1998：102-106.

[8]LIU Yufei,CUI Pingyuan. Observability analysis of deep-space autonomous navigation system[C]//Proceedings of the 25th Chinese Control Conference,Harbin,China,2006: 279-282.