城市交通枢纽短期客流量的组合预测模型

刘 杰 衡玉明 赵 辉 高学金 王 普

（1.北京公联交通枢纽建设管理有限公司 北京100161；2.北京工业大学电子信息与控制工程学院 北京100124）

0 引 言

目前我国正在大力发展以轨道交通为骨干，以公共汽车、电车交通为主体的，实现各类交通方式之间有机衔接的城市综合客运交通体系，以缓解城市客运交通的困境［1－2］。交通枢纽在城市综合客运交通体系中的主要功能是有效衔接各种交通方式，汇集和分配各种客流，满足乘客中转换乘时高效、安全、便捷、舒适的需要。城市交通枢纽的建设满足了居民的出行需要，然而枢纽内的客流量却呈现出了动态性的变化，客流量不仅影响交通枢纽的空间布局，同时也影响着枢纽内部的客流输送组织方案［3］。因此，对客流量进行短期的预测能够在一定程度上影响交通的组织方案和应急预案的调整，因而对客流量进行短期的预测是十分必要的。

1 问题分析

交通枢纽短期客流的时序性特点具有明显随机波动性，因此在众多的短期预测的模型方法中（主要包含指数平滑法［4］，灰色预测法［5］，神经网络［6］以及支持向量机［7－8］等），BP神经网络是具有适应性的简单单元组成的广泛并行互联的网络，具有良好的非线性，高度并行的处理机制［9］。使得网络具有较好的模式识别能力和在任意精度逼近非线性预测的能力。最小二乘支持向量机（LSSVM）是标准支持向量机（support vector machine，SVM）的1种扩展［10］，是建立在统计学习理论的VC维和结构最小化原理基础之上的方法，能够很好地解决有限数量样本的高维模型构造问题，且构造的模型具有很好的预测性能；可以解决小样本情况下的机器学习问题，具有良好的泛化能力；可以解决高维问题及非线性问题；人为设定的参数较少，便于使用。2种方法适合对交通枢纽的客流量进行预测。但由于交通枢纽客流量的影响因素较多，且相互之间的关系错综复杂，呈现的是1种极为复杂的高维非线性关系［11］，应用单一的预测方法往往具有片面性，不可避免地会降低预测精度。为提高客流量预测的精度，笔者采用了综合BP神经网络和最小二乘支持向量机的组合预测模型，即首先利用BP神经网络历史数据进行初步预测，再将初步预测的结果作为最小二乘支持向量机的输入，在此基础上进行训练和预测。

2 组合预测模型

2.1 BP神经网络预测模型

BP神经网络又称误差逆传播算法，是1种具有3层或3层以上的多层网络结构，每1层都由若干个神经元组成，且各层神经元之间通过不同的权重连接［12－13］，其结构图见图1。

BP神经网络的基本数学模型可表示为

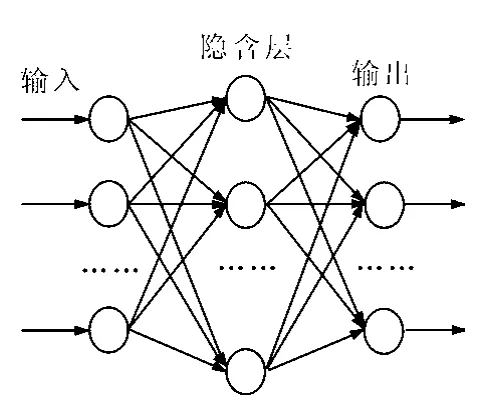
图1 3层BP神经网络Fig.1 BP neural network

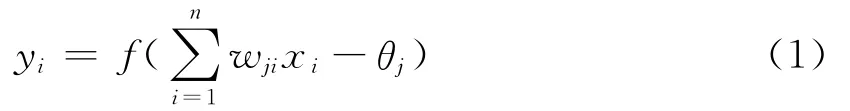
式中：wji为神经元之间的连接权；θj为神经元的阈值为神经元的激活值，再经过传输函数f就可得到输出值y，预测神经网络执行过程包括：训练过程和预测过程。所谓训练程，即BP神经网络按有导师学习方式进行训练，当学习模式提供给网络后，其神经元的激活值将从输入层经隐含层向输出层传播，在输出层的各神经元输出对应于输入模式的网络响应。然后按减少误差的原则，从输出层经隐含层回到输出层逐层修正各连接权。随着上述训练过程的不断进行，网络对输入模式响应的正确率也不断提高，而最终输出层的输出值即为所需的预测结果。

2.2 LSSVM预测模型

设给定的样本集为S＝｛（xi，yi），xi∈Rn｝（i＝1，2，…，l）。式中：xi为第i个输入数据；yi为相应于xi的目标输出；l为样本容量。那么最小二乘支持向量机预测问题就可转化为求解下面的最优化问题

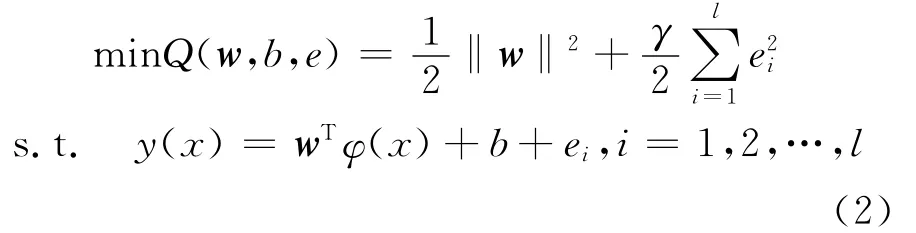
式中：φ（·）为核空间映射函数；w为权矢量；e为误差变量；b为偏差量；r为正规化参数（惩罚参数），r＞0。构造拉格朗日函数如下

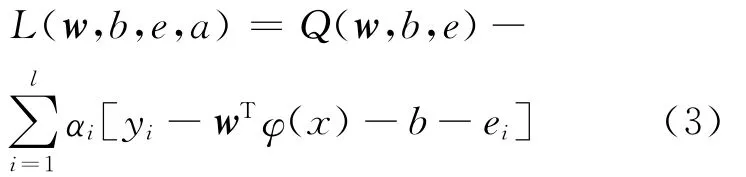
式中：αi（i＝1，2，…，l）为Lagrange乘子。将函数L分别对w，b，e，a求偏导，并令其为0，计算解得参数α（α＝α1，α2，…，αl）和b分别为

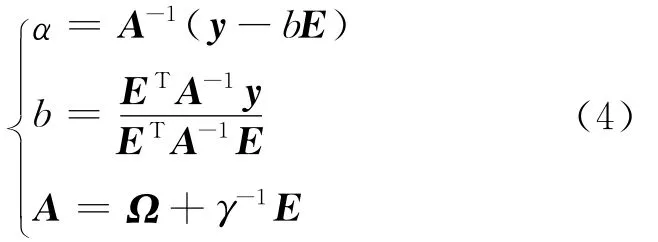
式中：y＝［y1，y2，…，yl］T，E＝［1，1，…，1］T，矩阵Ω的元素为

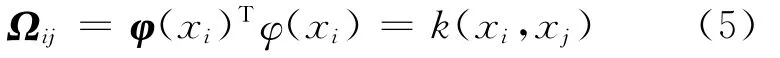
构造回归函数如下：

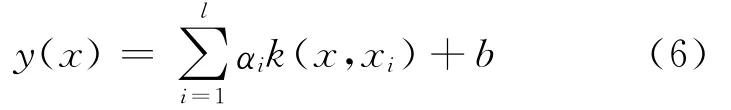
将参数代到式（6）即可得到LSSVM的预测结果，其中采用的核函数为径向基核函数。

2.3 组合预测模型

在上述2种模型中，神经网络具有很强的非线性映射功能，并具有并行分布式处理，自学习、自组织，以及良好的容错性等优点。然而神经网络的学习法采用经验风险最小化原理，不能使期望风险最小化，会出现局部极小点等问题，使得其在小样本，短期客流量的预测中效果不佳；而支持向量机方法运用结构风险最小化原则可解决神经网络所具有的一些缺陷，能够保证得到全局最优解，而且在训练样本很少的情况下具有很好的推广能力，在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势［14］，具有很强的泛化能力。

由于短期客流量的非平稳性特点，所以流随机性、不确定性更明显，导致短期客流量的预测要比长期预测受随机干扰因素影响更大，不确定性更强，规律性更不明显；单一的方法对于不同结构的数据样本，预测的差异性较大，导致预测效果的稳定性较差，从而影响预测的精度，为提高预测精度，消除单一方法带来的不确定性，采取了综合BP神经网络和最小二乘支持向量机的组合预测模型，将BP神经网络强大的非线性拟合能力与最小二乘支持向量机在小样本预测中的优势结合起来。首先利用BP神经网络对历史数据进行初步预测，再将预测的结果作为支持向量机的输入从而构建组合预测模型，具体结构见图2。

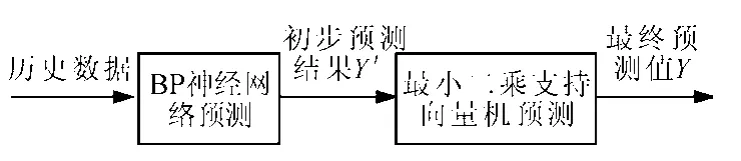
图2 组合预测模型Fig.2 Combination prediction model

3 仿真实验

为了验证文中算法在客流量预测中的有效性，采用2012年北京市东直门交通枢纽全年的实际客流量数据作为样本进行仿真实验，具体数据见图3。实验的评价指标采用平均绝对百分比误差MAPE和最大预测误差ME，即

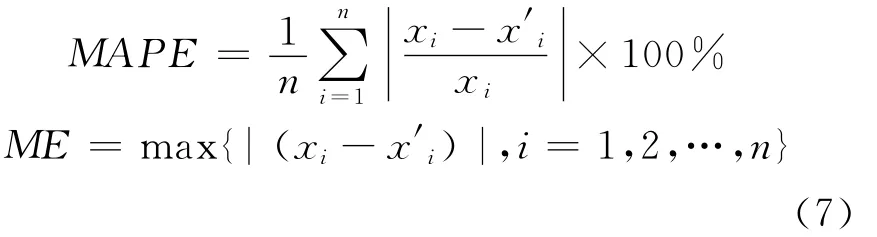
式中：xi和x′i分别为客流量的真实值和预测值；n为待预测样本个数。MAPE越小，表示模型的预测精度越高。

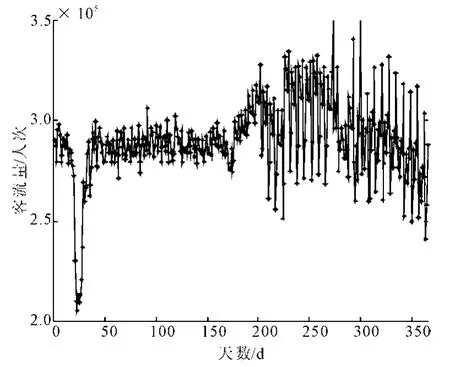
图3 东直门枢纽的客流量数据Fig.3 Passenger flow volume of Dongzhimen Transit Hub

具体实验步骤如下。

1）数据预处理。以1月1日到3月3日9周的数据为例（见图4），可看出第3周，第4周，第5周分别出现了异常的数据，究其原因这些异常点对应的日期为1月19日～2月1日，正处于春节期间，由于本文着重平日的短期客流量预测，因此将这些节假日异常点用其对应星期的其他周的平均数据代替，以完成数据预处理。同样对余下的客流量做相同的处理，并对新的时间序列做数据的归一化。

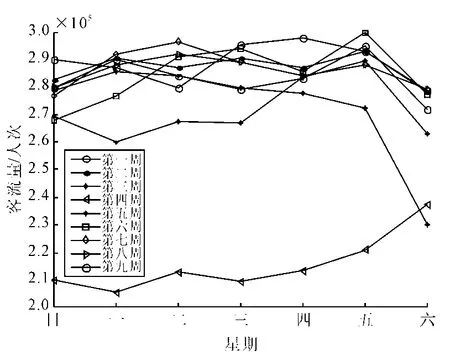
图4 九周的客流量数据（1月1日～3月3日）Fig.4 9－week passenger flow volume data

2）确定训练集与测试集。以数据时间（d）序列连续m的数据作为输入，第m＋1的数据作为输出组成1个新的样本集，包含了1个输入矩阵X和输出矩阵Y，确定测试集与训练集的比例r（测试集与训练集样本个数的比值），从而得到相应的训练集与测试集。

3）构建BP神经网络模型对训练集的样本进行初步训练和预测，得到历史的客流量预测值。

4）将BP神经网络得到的初步预测值作为最小二乘支持向量机的训练输入，构建模型对测试集进行预测，得到最终的客流量预测结果。

实验首先选取m＝3 d，r＝0.1的情况对数据进行预测，此时共有363个样本（前330个样本作为训练样本，后33个样本作为测试样本），得到预测结果见表1、图5。

表1 组合模型的预测结果对比Tab.1 Comparison prediction result of two models 人次

由表1，图5可看出笔者所提组合预测方法能够较好地与真实值相贴近，而为增加对比，采用BP神经网络与LSSVM 2种方法对表1测试集的数据进行预测并具体计算出其预测的平均绝对误差为：在m＝3，测试比例r为0.1的情况下，BP神经网络的平均绝对误差为：6.62%，LSSVM的平均绝对误差是：6.09%，而组合预测模型的平均绝对误差为5.95%，结果如表2所示。由表2可看出笔者所提组合预测方法的预测精度比LSSVM和BP神经网络的都要高，这直接验证了笔者所提方法的有效性，客流量的预测精度也得到了提高。

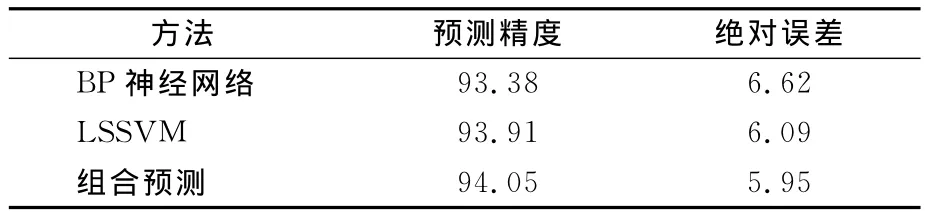
表2 笔者所提出方法预测精度与其他方法的比较Tab.2 Comparison result between the combination model and other methods

为了验证不同输入与训练比例对组合预测模型的精度的影响，笔者分别选取了m＝4，6，8；r＝0.1，0.3，0.5，求解了组合模型的预测精度并与BP神经网络与LSSVM模型进行了精度的对比，结果如表3所示。

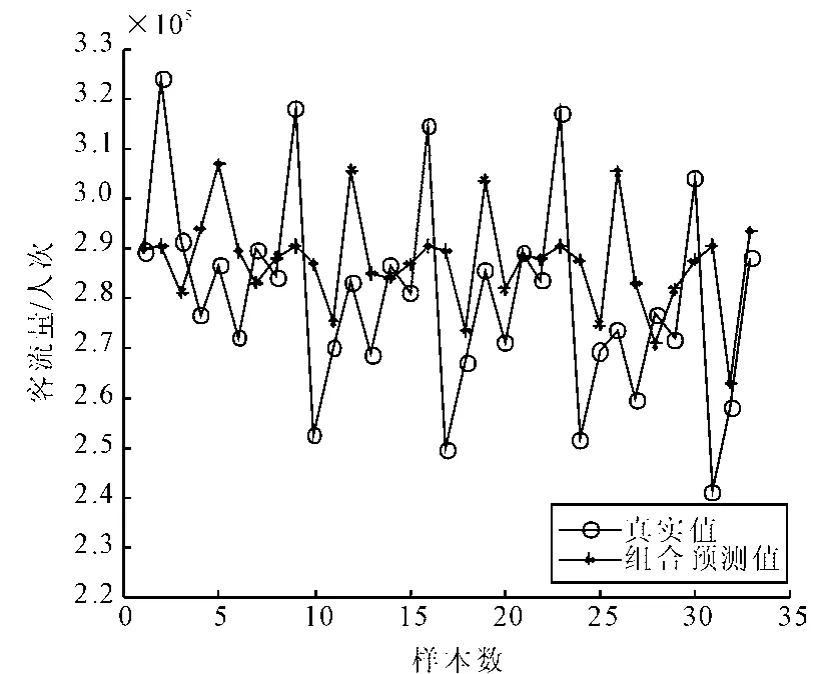
图5 2种模型的预测结果对比图Fig.5 Prediction result of two models

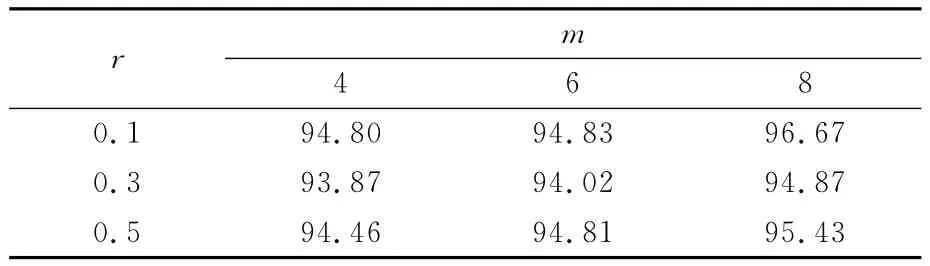
表3 不同输入与训练比例下模型的精度对比Tab.3 Prediction accuracy of the combination model in different situations %

由表3可见，不同的m与r值，模型的精度不同，总体来看测试集数量越小，精度越高，这是由于最小二乘支持向量机对短期小样本的预测问题具有优势，因此组合精度的输出会更高些。

4 结束语

针对交通枢纽客流量的复杂性，非线性等特点，笔者提出了综合BP神经网络和LSSVM的组合预测模型对客流量进行了预测，并采用了北京市东直门交通枢纽的实际数据作为验证，通过对比得知所提组合预测模型能够克服2种单一方法带来的不确定性，能够准确地预测交通枢纽的短期客流，且与其他2种模型相比，客流量的预测精度要更高些。后续的研究中将集中于改进BP神经网络以进一步提高客流量的预测精度。

［1］ 谭复兴.城市轨道交通概论［M］.北京：中国铁道出版社，2013.

［2］ 葛 亮，王 炜，邓 卫，等.城市公共交通枢纽客流量预测使用方法研究［J］.公共交通科技，2005，22（8）：110－113.

［3］ 邓军生，孔繁钰，陈小峰.基于SVR的轨道交通客流量预测［J］.重庆科技学院学报，2008，10（3）：147－149.

［4］ 刘罗曼.时间序列分析中指数平滑法的应用［J］.沈阳师范大学学报，2009，27（4）：416－418.

［5］ 吴 强，冯维琇，胡小嘉，等.灰色预测法在城轨客流预测中的应用［J］.城市轨道交通研究，2004，7（3）：52－55.

［6］ Kaan Yetilmezsoy，Ilter Turkdogan F M，Ilknur Temizel，et al.Development of ANN－based models to predict biogas and methane production in anaerobic treatment of molasses wastewater［J］.International Journal of Green Energy，2013，9（10）：885－907.

［7］ 石永辉，鲍 俊，严忠贞，等.混合智能算法在城市道路短时交通流量预测中的研究［J］.交通信息与安全，2011，29（4）：58－61.

［8］ Nicoletti M C，Bertini J R，Tanizaki M M，et al.Applications of evolutionary SVM to prediction of membrane alpha－helices［J］.Expert Systems with Applications，2013，40（9）：3412－3420.

［9］ 杨淑莹.模式识别与智能计算［M］.北京：电子工业出版社，2008.

［10］ 申富饶.神经网络与机器学习［M］.北京：机械工业出版社，2011.

［11］ 王艳辉，王 卓，贾利民，等.铁路客运量数据挖掘预测方法及应用研究［J］.铁道学报，2004，26（5）：1－7.

［12］ Cheng Hua Li，Xiang Ji Huang.Spam filtering using semantic similarity approach and adaptive BPNN［J］.Neurocomputing，2012（92）：88－97.

［13］ 林 连，林 桦.改进的BP神经网络在港口物流量预测中的应用［J］.交通信息与安全，2009，27（5）：161－165.

［14］ 杨兆升，王 媛，管 青.基于支持向量机方法的短时交通流量预测方法［J］.吉林大学学报，2006，36（6）：881－884.