卫星激光测距精度分析

李 博,李博宇,李兆南

(北京卫星导航中心，北京 100094)

0 引 言

激光测距作为高精度测距已成为无线电双向测距的有效检核手段，其精准性是科学研究、实验等诸多方面的基本物理参量[1]。

激光测距误差分为偶然误差和系统误差。卫星反射器分布所引起激光脉冲波形展宽和畸变带来的测距误差及测距仪器误差属偶然误差，如激光脉冲脉宽、时间间隔测量、收发信号探测、时间同步误差等。而对于不同激光脉宽和不同光电探测器所引起的质心改正值(CoM)、仪器系统的光电延迟的测量误差及气象参数采集及大气修正模型误差属系统误差。由于偶然误差不可控，所以主要通过修正系统误差来提高测距精度。

1 激光传播时延修正

1.1 大气延迟修正

大气修正的模型目前采用Marini-Murray模型。地平角高度20°时，估计误差约为5～10 mm.目前ILRS成立了一个研究组，正在深入研究此项修正，并希望解决更低高度的大气修正问题[2]。

当进行卫星激光测距时，激光脉冲通过大气到达卫星，经卫星反射后沿原光路返回测站。严格地说，在此过程中光脉冲的速度及方向都会因光脉冲到达的各点大气折射率的不同而不同。测距公式为

R=c·t/2 .

(1)

式中，c为真空中的光速，在大气中光速因折射率而变慢。大气折射率的变化将以两种方式影响光脉冲的传播，一是随大气密度而变的群折射率影响光速。也就是说光脉冲从测站射向卫星，其速度偏离了真空中的光速。二是大气折射率的垂直梯度，引起光的传播方向改变，使光线在大气“层”间发生弯曲，光线的轨迹是一条曲线而不是一条直线[3]，如图1所示。

图1 大气折射率壳层模型示意图

卫星与测站的几何距离为

Rg=-(RE+ht)cosθzen+

(2)

式中:RE为地球半径(取平均值6 378 km);ht为测站海拔高度;hs为卫星海拔高度；θzen为卫星天顶距。

卫星斜距测量值是沿弯曲的光线轨迹的积分：

(3)

式中:ng为光路径上任意点的大气群折射率;θ为信号路径曲线上所取的一个场点处的视天顶距。

由于大气垂直梯度的分布，故有Bouquer公式：

nrsinθ=n0r0sinθ0,

(4)

式中：n0是测站表面的大气折射率；n为光路径上的折射率。

大气延迟为

Ra=R0-Rg

(5)

大气相对群折射率为

Ng=(ng-1)×106.

(6)

在激光测距中，除测站点的折射率可以通过测量得到，光路径上其它各点的折射率是无法测量到的。所以，需要建立大气折射率模型来计算各点的折射率，以便进行大气延迟修正。

1.2 Marini-Murray大气折射改正模型

卫星激光测距中，目前普遍采用的大气延迟修正模型是1973年由Marini和Murray给出的，此模型假定大气层是由许多无限薄的同心壳层组成的，在此假定条件下，测距光路径上各点位于同一平面内，光路径上折射率的变化为一连续函数[4]。

Marini-Murray[1973]大气折射改正公式为

(7)

式中:P为大气压力(hPa);T为温度(°K);e为大气水汽分压(hPa);f(λ)为大气色散函数。在可见光波段，大气水汽分量对折射率的贡献与波长无关。

在Marini-Murray模型中，大气近似为理想气体，分压定律适用，并且大气物理参数随径向高度的变化规律假定服从流体静力学平衡方程。在此条件下，可以得到球对称大气误差修正SCMM：

(8)

式中:

F(φ,H)=1-0.0026cos2φ-0.00031H

A(PH,eH)=0.002357PH+0.000141eH

B(φ,TH,PH)=1.084×10-8PHTHK(φ,TH,

K(φ,TH,PH)=1.163-0.00968cos 2φ-

0.00104TH+0.00001435PH

其中:λ为激光波长(μm);E为卫星的仰角(°);φ为测站的纬度(°);H为测站海拔高度(m);PH为测站大气压(hPa);TH为测站大气温度(K);eH为测站水汽分压(hPa).测站水汽分压eH与大气表面相对湿度RH可以用Magnus公式表示

(9)

该模型的修正公式只需测量地面的大气压强、温度和湿度参数，就可以通过公式计算大气延迟量，其修正精度随仰角的增大而升高，对低仰角修正精度较差，原则上只适用于10°以上高度角的观测。

Marini-Murray公式与所用激光波长、大气物理参数、卫星仰角等有关，如图2所示。一般地说，对于相同仰角的不同卫星，大气延迟修正值差别不大，因为卫星的高度比较高(几百公里以上)，大气延迟主要发生在对流层与平流层内，高度在90 km以外的大气，密度甚小，对传播延迟几乎没有影响。

图2 Lageos卫星大气延迟修正随仰角变化关系

图2示出了以波长0.532 μm的绿光为测距激光，在通常大气表面参数下PH=1 000 mbar，TH=300°K，RH=50%,Lageos卫星随观测仰角变化的Marini-Murray模型的大气修正值。对Lageos卫星，当观测仰角为90°时，大气延迟值为2.45 m左右。当观测仰角20°时，大气延迟值约为7.0 m.对低仰角观测时，由于大气衰减大，修正公式误差也大，所以，应尽可能避免对低于20°的卫星的测距观测。

1.3 模型修正残差

由于大气分布极其复杂，难以用一个精确的解析公式来准确地修正大气延迟，所以修正值中必然带有误差，其误差来源于以下三个方面[5]：

1) 表面大气参数的测量误差。

2) 由于大气流动、复杂温度偏差等引起大气分层结构偏离了球对称假设。

3) 壳层模型中没有考虑横向梯度效应引起的误差。

图3示出了误差来源之一。在仰角20°时，大气压力测量值有1 hPa的误差带来8 mm的模型误差。如果大气压力测量值误差可以控制在0.3～0.4 hPa，对应的模型误差在仰角20°时，不大于3 mm，在天顶时仅为1 mm.大气温度与湿度测量误差，带来的模型误差在亚毫米量级。

图3 通过Marini-Murray模型计算的延迟修正误差

误差来源二和三均为水平不均匀带来的误差，由于大气并不完全符合流体静力学平衡方程，因此模型本身也存在一定的误差。当前卫星激光测距精度在厘米级，模型本身误差在毫米级，经实际观测结果证明：模型误差在允许范围内。

2 设备时延修正

2.1 影响设备时延的因素

设备时延包括测量系统的光路和电子设备引起的两部分时延。

SLR系统测量得到的距离是激光从主波取样探头产生的起始脉冲到回波探测器获得的关门信号之间的时间间隔。这两个探测点与仪器的相位中心不重合，带来了所谓光路时延，只要探测头位置不变，光路时延可视为常数[6]。

发射系统中，发射激光脉冲由PIN取样，经恒比鉴列器到时间间隔计数器开门，电子设备和电缆对信号产生时延。同样接收系统中回波信号经SPAD到计数器关门，也有时延。这部分时延是由设备的电子器件引起的，称电子时延[7]。电子时延与电子设备的响应时间、电缆长度、电缆接插件等因素有关，并随电子设备的工作状态而变，它是一个变化量。

为了修正设备时延，通常采用测量地靶来校准。

2.2 地靶校准

将地靶置于圆顶内，与望远镜距离约2～3 m，因此大气对地靶校正值几乎没有影响，为此近年来大多数台站广泛采用近地靶校准。如图4所示。

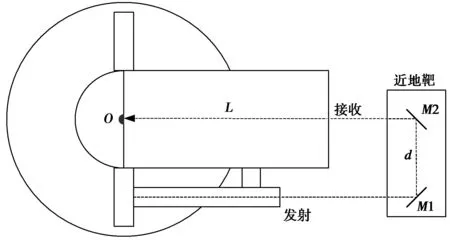
图4 近地靶校正示意图

近地靶采用两块反光板折光，所以接收到的信号光路径稳定，可以得到精度很好的校正值。O为望远镜相位中心参考点，M1、M2为地靶反射镜。测得的近地靶数据平均值减去L+d/2即为系统校正值。此校正值包含系统发射和接收光路的延迟以及电子线路的延迟，此延迟随温度变化，固在实际观测时每间隔1 h测一次地靶，以保证校正值的准确性。

3 结束语

激光测距误差主要存在于偶然误差和系统误差中，由于偶然误差不可控，通过修正系统误差的手段来提高测距精度。激光产生到发射口面及接收口面到计时器之间的光路和电路延迟总量可以通过测地靶的手段将这一部分误差从卫星测距过程中扣除掉，故不影响激光测距结果；观测站与卫星之间的光路传播时延通过建立Marini-Murray模型进行大气延时修正，当观测仰角过低时，大气衰减变大，修正公式误差增加，因此，应尽可能提高观测角度以便提高测距精度。

[1] 崔 鹏,史学舜，陈坤峰，等.基于光电延时法的激光测距精度测试系统[J].宇航计测技术,2011,2(1):57-61.

[2] 于彦梅.激光测距机及发展趋势[J].情报指挥控制系统与仿真技术,2002(8):19-21.

[3] 张承铨.国外军用激光仪器手册[M].北京:兵器工业出版社, 1989.

[4] 李建文.单颗导航卫星精密定轨与激光精度评估[J].武汉大学学报,2009,11(4):1276-1278.

[5] 王海先,叶 艾.大气衰减系数对激光测距能力影响的研究[J].舰船科学技术,2007,12(6):116-119.

[6] 许华冠.GPS卫星的激光测距和应用研究[J].天文学进展,1998，12(4):251-259.

[7] LIN C S,Cole TR dynamic model for global positioning system block IIR space vehicle[J].Journal of Spacecraft and Rockets,1997,3(3)：354-359.