北斗区域系统解算对流层天顶延迟比对分析

潘文超,郝金明,刘伟平

(信息工程大学,河南 郑州 450052)

0 引 言

卫星导航技术和现代通信技术的蓬勃发展,为空间定位技术带来了革命性的变化,开创了以GPS为代表的空基无线电导航定位技术的新时代。卫星导航系统作为一国的基础设施,不仅关乎国防安全和国计民生,同时拥有巨大的市场和广阔发展前景,世界各国都积极研制建设属于自己的卫星导航系统。中国作为卫星导航系统建设的后起之秀,随着2012年底北斗(BDS)区域系统正式投入运行,中国的卫星导航系统正稳步向全球系统迈进,针对北斗导航系统的应用和热点、难点问题将会掀起新一轮卫星导航系统研究高潮[1]。

卫星导航系统建设伊始,以它全球、全天候、高精度而广受关注,而影响卫星导航系统空间定位误差有很多:如在一定空间范围内,可以通过单差、双差等方法削弱空间相关性误差,如电离层延迟,对流层延迟,轨道偏差等;其他如天线相位中心,多路径误差等非空间相关性误差[2-3]。其中,与卫星信号传播有关的大气折射误差是全球导航卫星系统(GNSS)精密定位测量的主要误差源之一。产生大气折射误差的来源为电离层和对流层。电离层大气为弥散介质,可利用双频接收机准确计算出卫星信号在电离层中的传播延迟,从而达到消除电离层延迟误差。而对流层为非弥散介质,故无法采用双频观测值的方法来消除对流层延迟误差。

将对流层延迟分成天顶延迟和映射函数两部分是目前研究对流层延迟的最广泛也是最有效的方法。天顶延迟大小的确定以及计算的精度,将对后续的对流层延迟的确定产生较大的影响。同时对流层天顶延迟模型是气象元素的函数,在数值天气预报和GPS/MET有着广泛的应用[4]。因此很有必要对当前BDS解算对流层天顶延迟的精度进行比较和验证,为BDS区域系统乃至全球系统的进一步发展和应用,奠定坚实基础。

利用PANDA软件,对2013年多个站点的BDS原始观测数据进行解算,求得站点天顶延迟结果,并与相应GPS解算结果进行对比,分析当前BDS区域系统的稳定性和可靠性,以及下一步建设BDS全球系统需要改进的工作。

1 对流层延迟

1.1 对流层延迟

对流层延迟的主要影响:1)大气折射使传播路径弯曲,传播路径延长;2)电磁波传播速度被减慢。时间上的延迟等同于传播路径上的增加。

针对对流层延迟的研究可以追溯到20世纪中叶的无线电传播延迟改正,当电磁波在对流层中穿过时,传播速度将发生变化,路径也将产生弯曲。设对流层中的大气折射率为n,真空中的折射率为1.则信号传播路径上对流层延迟改正[5-6]

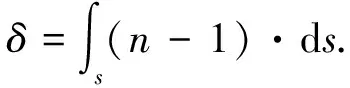
(1)

为了避免繁琐的积分程序,1954年Smith和Weintranb经过大量的实验得出模型,将对流层折射函数分为干气部分Nd和湿气部分Nw.在GPS后处理改正对流层误差时,若将所有信号传播路径上的对流层延迟作为未知量,会造成方程系数阵秩亏。于是有学者提出假设:任意方向上的路径延迟均与天顶方向延迟相关。将对流层延迟写为天顶延迟(ZTD)与映射函数(MF)乘积的形式为

(2)

对流层延迟数学理论方法的研究基本上可分为两大类,1)以Saastamoinen改正公式为代表,先将大气折射积分中的被积函数按高度角进行三角函数级数展开,再逐项积分;2)以Marini连分式映射函数和在此基础上发展起来的CFA模型为代表,采用数值积分方法求出对称大气模型下的不同高度角对流层折射延迟改正,再对积分值按高度角用一定的数学模式进行拟合,求出拟合系数[7]。

1.2 对流层天顶延迟

对流层天顶延迟可表示为折射指数沿天顶方向的积分[8]

(3)

式中:N(z)为大气折射指数; dz为沿测站天顶路径的积分元,可见天顶延迟是大气折射指数沿测站天顶路径的积分。现阶段减小对流层延迟影响的方法主要有三种:经验模型法,参数估计法和外部修正法。现有的天顶延迟和映射函数模型有很多种,主要有Hopfield模型、Saastamoinen模型、Black模型和EGNOS模型等[9-11]。其中映射函数是卫星高度角的函数。把ZTD与任意方向上的路径延迟联系起来。

将Hopfield的干模型误差式与Saastamoinen模型对比可知,压强测量误差的系数基本相同,而Hopfield模型却多出一个温度误差项,使得实践中Saastamoinen模型要比Hopfield模型改正结果好[12]。另外,Saastamoinen模型将温度梯度作为常数分层计算,而Hopfield模型只按单层计算,又定义了对流层高度值,对流层高度与测站纬度和季节有关,所以这个高度并不合适。因此许多GPS解算软件包括GAMIT和BERNESE都默认采用Saa-stamoinen模型[13]。采用Saastamoinen模型,求解BDS原始观测数据,得到相应ZTD值。

2 天顶延迟数据处理与结果分析

2.1 数据来源

选取信息工程大学分析中心提供的全球连续监测评估系统(iGMAS)2013年6月1日至6月30日(年积日为152至181)多个站点利用BDS和GPS原始数据解算的ZTD结果进行比对分析。解算的ZTD结果文件记录数据间隔为2 h,通过比较分析,剔除BDS和GPS不共有的站点,同时顾及北斗区域系统覆盖的地区以及南北半球站点分布,站点的比对性,选取了其中的6个站点共30天的数据。这6个站点包括三个IGS站,分别是BRST(法国),GMSD(日本)和REUN(法国);三个非IGS站CUT0(澳大利亚),DHAB(阿联酋)和HKTU(香港)。

2.2 数据处理和结果比对分析

通过对站点数据的合并筛选,得到6个站点单独每天的ZTD观测数据和6个站点单独的所有天的ZTD解算结果。导入MATLAB中,计算绘图。将BDS和GPS一个月内每天间隔为2 h的ZTD解算结果进行比较,如图1所示。

同时,以GPS解算结果为真值,对每个站点的BDS和GPS解算ZTD结果进行做差,得到BDS解算ZTD的差值曲线,如图2所示。

比较图1可知,BDS在6个站点均能显示出ZTD值变化趋势,对急剧的天气变化均能很好展示。在BRST、CUT0、DHAB和GMSD四个站点的ZTD解算值BDS和GPS基本符合的很好,只有CUT0站点年积日172以后BDS解算的ZTD出现了较大的波动。而HKTU和REUN则相差较大,在HKTU站点的BDS解算的ZTD值均小于GPS解算值,REUN解算值出现了较大偏差,尤其是在179,180,181这三天的最大差值接近1 dm.由图2,BDS解算的ZTD与GPS的差值76%位于±2 cm之间,而位于之间的差值不到50%.CUT0 、HKTU和 REUN站点差值波动较大,大部分在±6 cm之间。

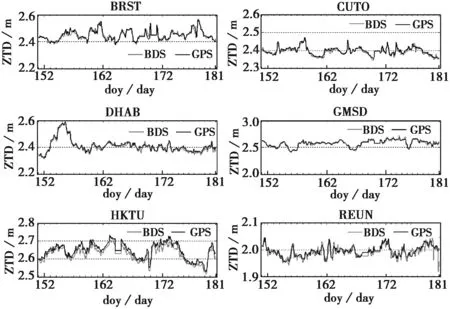
图1 6个站点BDS与GPS解算ZTD结果比较

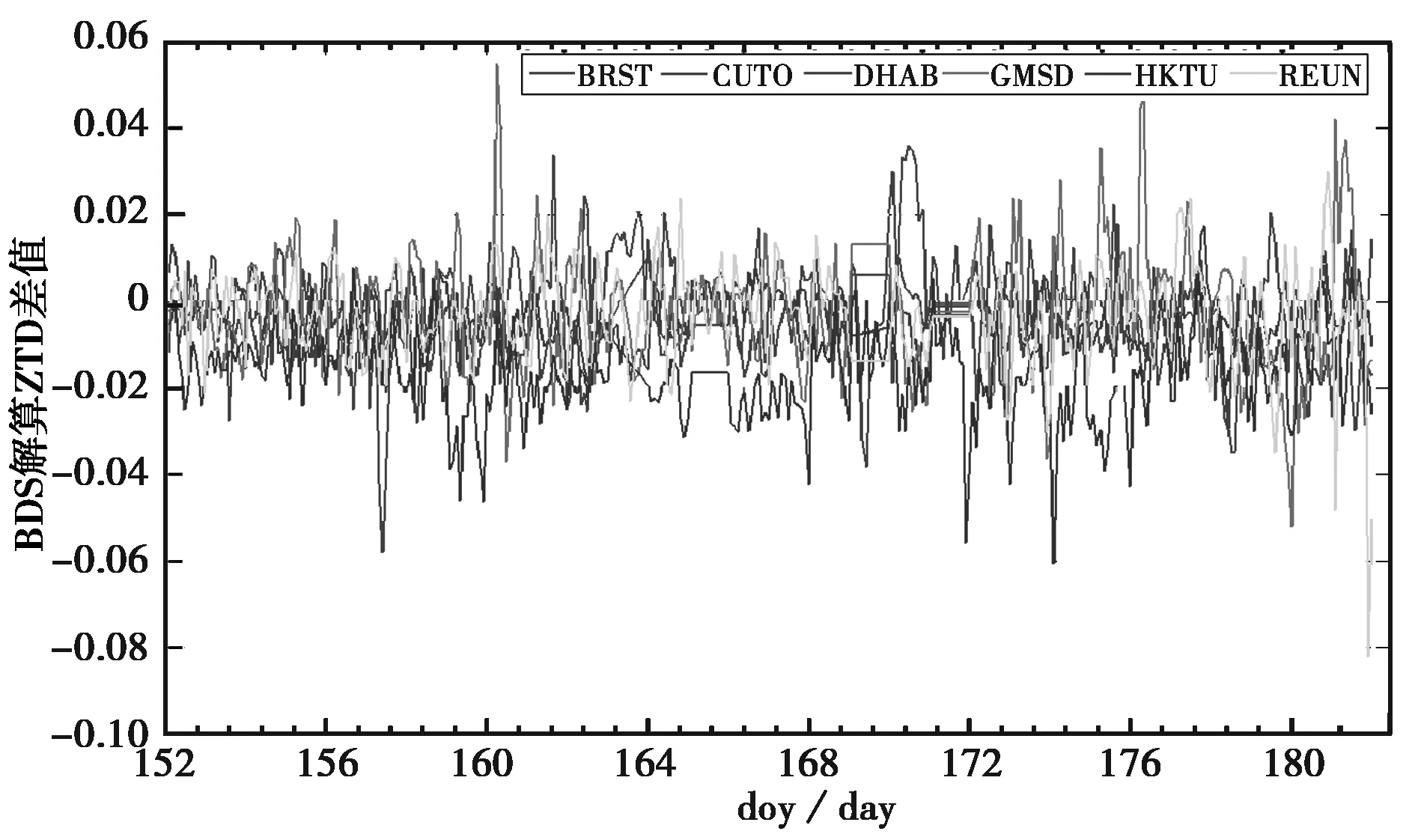
图2 6个站点BDS解算ZTD差值

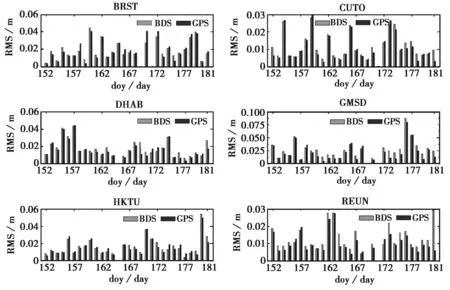
图3 BDS和GPS解算ZTD中误差比对

同时,对BDS和GPS解算的每天ZTD的中误差进行了比较,如图3所示,可以看出除了REUN站点二者解算ZTD每天中误差相差较大外,其它5个站点二者相差均不大,在位于中国香港的HKTU站、日本的GMSD站和阿联酋的DHAB站,二者解算的RMS变化均较平稳,其余三个站点变化较大。

通过上述分析比较可知,现阶段北斗区域导航系统已经基本具备全球系统的一些功能,在面对全球多个地区不同站点的解算的ZTD均可以投入实际使用,但相对于GPS而言,在精度、稳定性和可靠性上有待进一步的提高。同时出现上述问题的可能原因:1)在站点数据选择和时间段选择上,由于6月份全球水汽丰富,天气变化剧烈,对流层湿分量变化较大(目前众多改正模型对干分量的改正精度较高可达90～95%,而对湿分量的改正精度只能达到10～20%),BDS解算的ZTD出现较大的误差; 2)选取的站点距离中国较远,现阶段的区域星座分布还无法满足全球ZTD解算的精度要求; 3)由于北斗现阶段主要是针对区域服务进行优化,因此相比较GPS全球系统而言,仍有大量工作需要改进。

3 结束语

通过比对可以发现,北斗区域导航系统在解算ZTD时已经初步具备全球系统的能力,在中国周边地区已经具备和GPS相同的解算水平,在面对剧烈的天气变化时可获得与GPS相同的可靠性,但在精度和稳定性上有待进一步的提高。下一步的工作主要有:1)选用中国周边的多个站点的长期观测数据,进一步分析验证北斗区域系统的精度、稳定性和可靠性,同时积极做好全球系统的铺垫工作。2)参考成熟的GPS对流层延迟改正方法,建立适合北斗导航系统的中国乃至全球的对流层改正模型。

致谢感谢信息工程大学分析中心提供的全球连续监测评估系统(iGMAS)对本文工作的帮助和支持!

[1]杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6.

[2]李浩军,王解先,胡丛玮.GPS对流层延迟的历元间差分分析[J].同济大学学报, 2010,38(3):448-452.

[3]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005年.

[4]张双成,叶世榕,刘经南,等.动态映射函数最新进展及其在GNSS遥感水汽中的应用研究[J].武汉大学学报·信息科学版,2009,34(3):280-283.

[5]李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009年.

[6]张双成,张鹏飞,范朋飞,等.GPS对流层改正模型的最新进展及对比分析[J].大地测量及地球动力学,2012,32(2):91-95.

[7]丁晓光.对流层延迟改正在GPS数据处理中的应与研究[D].西安:长安大学,2009.

[8]殷海涛. 基于参考站网络的区域对流层4D建模理论、方法及应用研究[D].成都:西南交通大学,2006.

[9]AHMES M M, SULTANA Q,REDDY A S,etal. Tropospheric error correction in assisted GPS signals[J].India Journal of Radio & Space Physics,2013:159-166.

[10] HONMA M, TUMURA Y, REID M J,etal.Tropospheric delay calibrations for VERA[J]. Astronomical Society of Japan,2008:951-960.

[11] KHAYKIN S M, POMMEREAU J-P, HAUCHECOME A. Impact of land convection on temperature diurnal variation in thetropical lower stratosphere inferred from COSMIC GPS radiooccultations[J]. Atmosphric Chemistry and Physics, 2013:6391-6402.

[12] 黄丁发,周乐韬,李成钢,等. GPS增强参考站网络理论[M].北京:科学出版社,2011.

[13] XU Guochang. GPS theory algorithms and applications [M].2 ed. Heidelberg:Springer Berlin,2007.