组合导航中一种新息自适应卡尔曼滤波算法

薛文婷,张 波,李署坚

(北京航空航天大学电子信息工程学院,北京 100191)

0 引 言

卡尔曼滤波是在组合导航中常用的信息融合算法,使用标准卡尔曼滤波的前提条件是系统的动力学特性和噪声的统计特性已知,但在实际情况中由于全球定位系统接收机与航位推算(DR)器件及外部环境变化导致的不确定噪声使得这个前提不能满足,常导致滤波发散[1]。要控制发散首先需要判断系统所处的不稳定状况,然后选择不同的发散控制方式,新息可以用来作为判断和调整滤波器增益的依据[2]。目前,国内外对于自适应卡尔曼滤波器的研究逐渐集中在两个方面:基于新息自适应估计(IAE)[3]的卡尔曼滤波器和多模型卡尔曼滤波器(MMAE)[4]。本文提出了一种基于IAE的卡尔曼滤波算法,可以通过实际新息的量测计算直接实现修正卡尔曼滤波增益,提高了在GPS测量发生较大变化时卡尔曼滤波器的精度和鲁棒性[5]。通过仿真实验对比分析了这种方法与传统卡尔曼滤波方法的定位误差,研究结果表明基于新息的卡尔曼滤波具有优于传统卡尔曼滤波的定位结果且不易发散。

1 IAE尔曼滤波算法

1.1 卡尔曼滤波新息的概念

离散卡尔曼系统有以下两个方程

Xk=φk,k-1Xk-1+Γk,k-1Wk-1，

(1)

Zk=HkXk+Vk，

(2)

式中:Xk为n维状态向量;φk,k-1为n×n阶状态转移矩阵;Γk,k-1为n×p阶干扰矩阵;Wk-1为p维系统噪声向量;Zk为m维观测向量;Hk为m×n观测矩阵;Vk为m维观测噪声向量。假定Wk与Vk为相互独立的零均值白噪声序列,分别有协方差阵

cov[WkWj]=Qxδkj，

(3)

cov[VkVj]=Rkδkj.

(4)

假定系统为一致完全能观和一致完全能控,则滤波是稳定的,激荡滤波递推充分多步以后,滤波误差协方差阵Pk,k将趋于常数矩阵P+,增益矩阵Kk将趋于常数矩阵K,预测误差协方差阵Pk,k-1将趋于常数矩P-,它们之间关系为

P-=φP+φT+ΓQΓT，

(5)

K=P-HT(HP-HT+R)-1，

(6)

P+=(I-KH)P-，

(7)

(8)

式中:rk为预报残差,通常称为新息,描述了滤波器的观测量的估计值与实际观测量之间的差值。

1.2 改进的IAE卡尔曼滤波算法

以新息方式列写卡尔曼滤波算法,状态的一步预测为

(9)

状态估计

(10)

滤波增益矩阵

(11)

一步预测误差方差阵

(12)

误差估计方差阵

Pk=(I-KkHk)Pk,k-1.

(13)

滤波器的新息序列rk状态和其新息方差Crk的表达式为

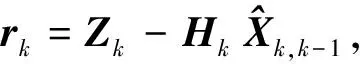
(14)

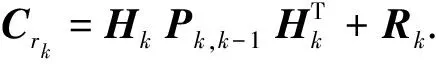
(15)

(16)

基于零均值白色滤波新息更新序列,滤波的统计新息矩阵的更新方程为

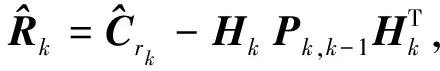
(17)

(18)

式中:Δxk=Kkrk,将式(15)带入式(11),即得改进的IAE自适应卡尔曼滤波增益的计算公式为

(19)

图1 IAE卡尔曼滤波算法流程框图

2 GPS/DR组合导航模型

本算法将GPS/DR信息进行集中处理,运动模型为当前统计模型。即当前机动目标在以某一加速度机动时,它在下一瞬间的加速度取值是有限的,并且在当前加速度的领域内呈现某种统计分布。状态量一般选取位置信息或位置差信息、速度或速度差信息、加速度或加速度差信息,便于直观观测运动状态的变化。DR系统一般选取陀螺仪和里程计作为航位推算部分,考虑在状态量中加入DR设备量,且知道陀螺和里程输出均为单位时间内变化量,所以考虑加入陀螺和里程 误差量作为状态量的一部分。

系统的状态量选为

将GPS接收机输出的定位信息er、en以及陀螺仪的输出θ和里程计的输出s作为外部观测量。

当前时刻状态量与前一时刻状态量及当前时刻观测量之间的关系表示为

X(k)=Φ(k,k-1)X(k-1)+μk,

(20)

Z(k)=H(k)X(k)+εk.

(21)

H[X(k,k-1)]=

3 仿真结果

对改进的新息自适应卡尔曼滤波算法进行仿真验证,设定仿真条件为:接收机三轴定位误差均为20 m, 接收机量测误差方差为10 m, 接收机采样周期为1 s,陀螺零漂为0.05(°)/h,里程计零漂0.05,东向和北向机动加速度误差方差1.5 m/s2,误差相关时间0.1,东向和北向位置误差相关时间设为0.01,微机械陀螺误差和里程计误差相关时间均为1 000 s,仿真时间设定为2 000 s,陀螺误差均方差0.1°/h,里程计误差均方差2 m.车辆沿着东北方向变加速行驶,初始速度为10 m/s,仿真时间1 600 s,采样周期1 s.为观测系统对外部量测干扰的效果,对GPS观测数据进行加噪处理,做如下设定:测量误差选择三种不同强度的误差,1～300 s取1倍的观测误差,301～600 s取4倍的观测误差,601～900 s取9倍的观测误差,之后量测误差恢复为1倍。常规的卡尔曼滤波算法模型始终采取预先设定的量测误差。改进的自适应卡尔曼滤波采取有限记忆的滑动新息方差,数据窗口大小N=20,以改进卡尔曼增益K的计算。滤波效果如图2～图4和表1所示。

图2 一般卡尔曼滤波位置误差与观测误差

图3 改进IAE卡尔曼滤波位置误差与观测误差

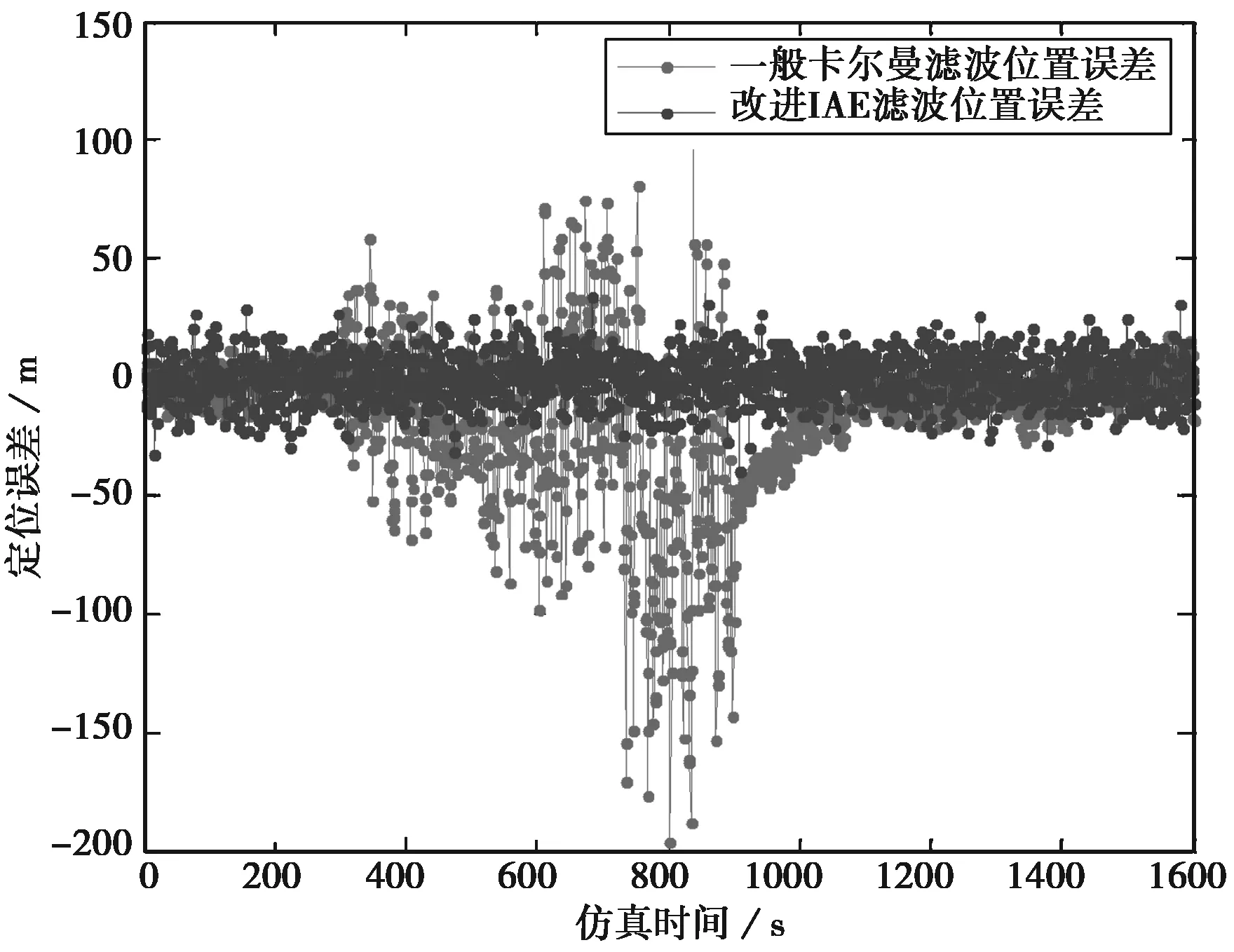
图4 联邦卡尔曼滤波与改进的IAE滤波

表1新息自适应卡尔曼滤波与联邦卡尔曼滤波算法位置误差统计特性

与参考轨迹的误差范围/m新息自适应卡尔曼滤波联邦卡尔曼滤波 小于1050.12%17.26% 小于2081.55%32.96% 小于3094.06%56.54% 小于40100%62.32% 小于50100%76.89%

4 结束语

在系统量测噪声较大时,改进的新息卡尔曼滤波算法仍能保持较好的滤波效果,而传统卡尔曼滤波算法则随量测噪声的变化出现了较大的发散,证明改进的新息自适应卡尔曼滤波算法能根据外界噪声变化自适应的调整滤波,在系统噪声增强时候可以保持优于联邦卡尔曼滤波的定位精度及稳定性。

[1]李 旦.组合导航自适应卡尔曼滤波改进算法研究[J].测控技术,2011,3:114.

[2]卞鸿巍，李 安，覃方君，等.现代信息融合技术在组合导航中的应用[M].北京:国防工业出版社.2010.

[3]MOHAMED A H, SCHWARZ K P. Adaptive Kalman filtering for INS/GPS[J]. Journal of Geodesy, 1999, 73(4):193-203.

[4]LOEBIS D, SUTTON R, CHUDLEY J,etal. Adaptive tuning of a Kalman filter via fuzzy logic for an intelligent AUV navigation system[J]. Control Engineering Practice, 2004, 12(12):1531-1539.

[5]卞鸿巍,杨艳娟，金志华，等.基于GPS姿态量测系统的综合导航系统研究[M].弹箭与制导学报,2003,23(5):8-11.