惊讶事件的证据力探析
2014-08-20杜文静
杜文静
(华东政法大学人文学院,上海201620)
关于科学理论的形成过程,爱因斯坦(Albert Einstein,1879-1955)说:“由经验材料作为引导,研究者提出一种思想体系,一般来说,它是在逻辑上从少数几个所谓公理的几个基本假定中建立起来的。我们把这样的思想体系叫做理论。”[1]115柯匹(Irving M.Copi,1917-2002)和伯吉斯-杰克逊(Keith Burgess-Jackson,1957-)提出了科学研究有七大步骤,即:问题、预备假说、收集额外事实、形成假说、演绎进一步后承、检验后承和应用,因此,科学研究被定义为从可观察的事实或经验到那些事实之合理解释的任何推理[2]249~257。换句话说,科学研究离不开推理,也离不开逻辑。其中,推理主要是归纳推理和概率推理,而逻辑主要是归纳逻辑和概率逻辑。如我们所知,归纳逻辑与概率逻辑是科学逻辑的核心组成部分,而归纳推理和概率推理的评价都不离开证据。卡尔纳普(Rudolf Carnap,1891-1970)在区分了三个确证语义概念基础上给出了确证证据的定义,探讨了确证证据的一般形式[3]79。当然,惊讶事件(surprising events)的证据价值是我们无论探讨科学证据还是法律证据都不应当回避的问题。但在本文中,我们不打算从科学证据角度为惊讶事件的证据力进行合理性辩护,只试图在霍里奇(Paul Horwich,1947-)给出的惊讶事件的定量描述定义以及相对性思想基础上,通过惊讶事件的刑事侦查证据力来为霍里奇的惊讶事件定义进行合理性辩护。
一、确证、验证与惊讶事件
卡尔纳普把波普尔(Karl Popper,1902-1994)的“验证度”(Grad der Bewährung/degree of corroboration)译成“证成度”(degree of confirmation),而且在他俩之间还有过专门讨论,波普尔曾被卡尔纳普说服并放弃了自己的概念,但后来因为卡尔纳普把“确证度”与“概率”视为同义语而使波普尔又捡回自己原有的概念。不管是波普尔的“验证度”还是卡尔纳普的“证成度”,都与概率密切相关,甚至卡尔纳普把“确证”与“概率”看作同义语[4]249。由此可见,要讨论霍里奇的惊讶事件定义理论,必然离不开卡尔纳普的“确证”与波普尔的“验证”。当然,我们在此并不想深究波普尔和卡尔纳普的孰是孰非,而只关注惊讶事件与确证和验证的密切联系,因此,我们暂且采用卡尔纳普的部分观点,即确证与验证是同义语。
一个理论要获得信任和支持,就必须得到经验材料的确证或验证。在科学确证理论中,如果一个理论或假说能够推断或解释某一经验陈述为真并且该陈述在当时背景环境下被公认为真,则该陈述就构成了人们信任这个理论的一个理由,或者说这个陈述提供了一个确证或验证了该理论的证据。然而,从直观上讲,在当时背景环境下,假如一个理论能够预测到令人惊讶的事件,则为该理论的信任提供了很强的支持力,也就是说,如果一个理论能够预测一些在当时背景环境下被认为是不可能的事情,或者能够解释当时背景环境下一些离奇的、异常的现象,那么这个理论将获得人们更多的支持。
到底什么样的事件会令人感到惊讶?通俗的解释是当人们确信不可能的事情却实际发生了,就会让人感到惊讶。由于这种非常确信不会发生的事情却实际发生的概率都是非常小的,因此,惊讶事件一定是小概率事件。霍里奇根据主观概率给出惊讶事件的定量描述定义:
【霍里奇定义】在一定的背景环境下,令C表示在该背景环境下产生的信念,令E表示可能令人惊讶或可能不令人惊讶的陈述,那么,必要条件是在信念C下产生P(E)≈0,并且一个更强的条件是P(C/E)<<P(C),E才是惊讶的,即事件E为惊讶事件[5]101。
通俗地讲,根据霍里奇的观点,如果P(E)≈0[即条件(1)]且P(C/E)<<P(C)[即条件(2)],其中C代表假定的背景环境信念,那么事件E就是惊讶事件。换句话说,在给定的背景环境C下,事件E几乎不可能出现;一旦事件E发生,信念C的概率实质地减少了。
后来,霍里奇的这一定义被曼森(Manson)与思拉什(Thrush)[6]、奥尔森(Olsson)[7]以及怀特(White)[8]等人支持和应用。曼森和思拉什在论述“宇宙微调论”时,根据霍里奇惊讶事件的定义,解释了为什么星星、银河系、生命的出现让人很惊讶。奥尔森利用霍里奇惊讶事件解释了在证人协议中,低先验概率蕴含着低后验概率,从而说明了科恩(Cohen)的证人协议理论并不是普遍有效。怀特借助霍里奇惊讶事件说明了“宇宙微调论”和“多重宇宙假说”的关系。另一方面,当确信会发生的事情而实际未发生,人们也会感到惊讶!然而这种事情却是高概率事件。不过,它与霍里奇的定义并不矛盾,因为霍里奇的惊讶事件定义是为了确证一个理论,并为信任该理论提供一个强有力的证据支持。当一个理论或假说能够成功地解释或预测一些几乎不可能、令人惊讶的事件,人们当然会更加相信、更加接受该理论或假说。而非常确信会发生但实际未发生事件也确实令人惊讶,但是当一个理论或假说能够蕴涵这种高概率发生的事件而实际却未发生时,它只能是证伪了该理论,从而为该理论提供了一个强烈的证伪证据。可见,奥尔森对证人协议理论的说明与霍里奇的惊讶事件在本质上是有所不同的,因为它们用于论证的目标恰恰相反,但并不相悖。
二、哈克尔对霍里奇定义的改进
根据霍里奇的定义,惊讶事件E不是一个绝对概念,而是一个相对概念。事件E的出现令人惊讶,是相对于一定的背景环境信念而言的,并且在该背景环境信念下,事件E发生的概率非常小。比如将一颗“均匀的”骰子独立地投掷60次,如果连续60次都出现点数6,人们会对这个投掷结果感到惊讶不已,因为对于此时的背景环境C为“均匀的骰子”而言,连续出现60次点数6这个结果序列的概率非常小,该概率仅为(1/6)60。
可是,并非所有小概率事件都会令人惊讶。根据惊讶事件条件(1),只有小概率事件才是惊讶事件,换句话说,小概率是惊讶事件的必要条件。再以前面的骰子投掷为例。
“在连续60次投掷过程中,一个由点数1、2、3、4、5、6各出现10次构成的投掷序列”概率仍是(1/6)60,然而该结果却符合人们的主观预期,因此,人们对这次投掷结果并不会感到惊讶。
一个理论或假说所预测的资料E具有很小的先验概率,主要有下列两种情形:其一,另一种被强烈信任的理论几乎蕴含E为假;其二,没有理论给E提供更多的信任凭证,并且E是许多可能实验结果中的某一个,例如温度中的某个值。然而,仅在第一种情形中,资料E的发现是令人惊讶的。人们之所以对前者感到惊讶,是因为前者满足惊讶事件条件(2),而后者却不满足,因此条件(2)排除了某些不会令人惊讶的小概率事件,使得惊讶事件的定义更加合理化。
在霍里奇的定义中,条件(1)的验证很容易实现,通常是在背景环境C下赋予事件E一个很小的主观概率,但条件(2)却比较难验证。霍里奇构造了对背景环境的另一可能的备选假设K,通过验证比较容易判断的条件:

然后,用它来验证条件(2),这是因为如果(*)式满足则一定下列公式成立。
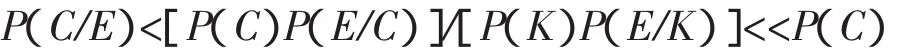
进而,P(C/E)<<P(C)得到了满足,这样事件E就是一个惊讶事件。当我们去验证一个事件是否为惊讶事件时,备选假设K1的存在与选择对于验证霍里奇定义的条件(2)具有至关重要的作用。为了验证条件(2),人们急切地需要寻找对背景环境的另一个可能的备选假设K2,且K2能使E更可能发生,甚至几乎可以蕴含事件E为真。
可是,在哈克尔(David Harker)看来,并不是对所有惊讶事件的例子都能找到这样的备选环境假设,并且有些对备选环境假设的解释是违反事实的,甚至是错误的。例如,大部分人对“生日问题”会感到惊讶,即在23个人中,有两个人生日相同的概率超过50%。在这个例子中,人们就无法找到相应的备选环境假设K。哈克尔认为霍里奇对惊讶事件的定义是有问题,他指出惊讶事件应该是小概率且与人们的期望相冲突的事件。于是,哈克尔对霍里奇的定义作了一些修改,并给出了如下定义:
【哈克尔定义】在一定的背景环境C下,如果它同时满足三个条件:
(1)P(E)≈0;
(2)P(A/C)高,其中A表示感到惊讶的个体的某种期望或信念;并且
(3)P(A/E)≈0,
则事件E为惊讶事件[9]。
因此,哈克尔将这三条判断标准概括为:一个事件E是惊讶的,如果E在认识论上是不可能的,并且E不能用符合人们预期的方式忠实地描述。在生日问题中,人们要以50%的概率保证一群人中有两个人生日相同的预期总人数要远远超过23人,所以按照哈克尔的定义,生日问题是一个惊讶事件,而对霍里奇来说,生日问题却无法解释。
哈克尔对惊讶事件的定义虽然能解释更多的让人感到惊讶的事例,但他的定义太过依赖于感到惊讶个人的期望,过于主观,因此,其证据力较弱。例如,在连续投掷一枚均匀硬币100次的试验中,背景环境信念C是“均匀的硬币且投掷也是公平的”,这样任意一个特殊的投掷结果序列出现的概率都很低,且都等于(1/2)100。令E表示“连续出现100次人头”这个结果序列,令A1表示期望“出现人头的次数在40到60次之间”,则P(A1/C)很大,且P(A1/E)=0,所以E是一个惊讶事件。但是,如果令A2表示期望“出现人头的次数在0到100次之间”,则P(A2/C)高,但P(A2/E)=1,不满足哈克尔的条件,所以E“连续出现100次人头”又不是一个惊讶事件。
哈克尔进一步提出,惊讶事件并不要和每个期望都相冲突,只要事件和一个期望相冲突,那么它就是惊讶的。不过,我们认为,哈克尔的这一说法正说明他的定义具有很大的主观性和随意性。相比较而言,我们认为,尽管霍里奇的定义无法解释某些人感到惊讶的事情,甚至不承认某些人感到惊讶的事情是惊讶的,但他的定义条件更强、更客观。对霍里奇来说,事件E的出现是惊讶的,仅当在背景环境信念C下,事件E似乎不可能发生,且在事件E发生的条件下,背景环境信念C的概率实质性地缩小了,即P(C/E)远远小于P(C)。背景环境信念C的概率实质性地缩小,这一要求不依赖于感到惊讶个人的主观期望,客观性更强,要求也更严格。所以,尽管霍里奇定义的惊讶事件的范畴更小,但是恰恰这种要求严格的惊讶事件却更具有独特的证据价值。
三、惊讶事件的证据学意义
一个理论或假说能精确地预测或解释惊讶事件,为什么将获得更强的支持和信任?我们的回答是:
【惊讶事件的证据力】惊讶事件的证据力主要取决于:
(1)惊讶事件的出现与人们在一定背景环境下对该事件主观想法形成巨大的反差,更容易引起人们的警觉和重视;
(2)惊讶事件是小概率事件,对于确证该理论具有很高的确证度。
根据科学确证的概率含义:在背景环境信念C下,证据E提供信任假说H的理由大于信任假说J的理由,仅当在背景环境信念C下,有P(H/E)/P(H)>P(J/E)/P(J)成立。利用贝叶斯公式,可以得到:
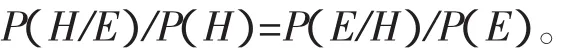
由于假说H能预测到惊讶事件E,所以P(E/H)=1,从而
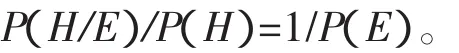
根据霍里奇的定义,惊讶事件E的概率相当低,从而P(H/E)/P(H)一定高,所以惊讶事件E的出现极大提高了理论或假说H为真的可能性。所以,惊讶事件E对H具有很高的确证度和支持度。
首先,让我们利用案件“新娘之死”来展现惊讶事件在刑事侦查中可以为公安人员快速找到案件突破口的逻辑魅力所在。2013年7月7日,中央一台“今日说法”栏目播出了一宗名叫“新娘之死”的案件。在这个案件的侦破过程中,惊讶事件是警方成功破案的突破口,为警方提供了重要的线索指引。下面,我们先还原该案件的基本案情:
【基本案情】2013年3月16日上午11点到12点之间,在上海嘉定区,一位刚结婚5天且怀孕不久的新娘小丽在家中被人活活掐死,并遭到纵火焚尸灭迹。根据警方各方侦查取证,最终将嫌疑人锁定为这两个人:小丽的丈夫杨亮,以及小丽夫妇公司的前一天刚辞职的司机翟雪锋。然而,根据杨亮和翟雪锋对他们当天行踪活动的陈述,并通过警方一一核实之后,警方发现他们都没有作案时间,都有不在作案现场的证据。
正当案件陷入僵局的时候,有一个细节引起了警员沈超锋的怀疑,那就是翟雪峰对自己当天的行踪刻画的每一点、每一个细节都非常清楚、准确。翟雪峰说他当天上午10点50分左右离开家里,然后出去找工作,他然后还能具体说出在哪条路上,哪家厂门口,看到什么样的招工信息,招工信息上有哪些具体的要求。这些信息经过警方一一核实之后,除了他离家时间应该是上午9点多钟外,其他信息完全吻合。超强的记忆能力和清晰的行踪陈述不得不让人“惊讶”,也不得不引起人们的怀疑。
一个人的记忆如果能够强化到这个程度,那就是他在有意地回避某些东西,或者刻意在规避某种风险的程度下,他才会讲得如此清楚。在这里,超强的记忆能力和如此清晰的行踪陈述就是一个“惊讶事件E”,因为在现有背景环境C“人的记忆力不可能如此精确”下,一个人在正常情况下,不可能把自己的行踪记得如此清楚,除非他是刻意要记下自己的行踪。正是因为这个令人“惊讶”的超强记忆力,警方提出假说H“翟雪峰在说谎”。
于是,警方对翟雪峰当天的行踪作了进一步的核实。核实发现,翟雪峰所说的当天12点左右在金园八路看到的一家招工启事,事实上是当天下午2点多钟才张贴出来的。这时,翟雪峰才露出马脚,原来他为了制造没有作案时间的证据,自己当天下午刻意去踩点,把那些找工作的行踪记得非常清楚。但百密一疏,时间上碰不上,细节上有出入,翟雪锋一直在说谎。后来,经过警方进一步多方取证,证实了犯罪嫌疑人就是翟雪峰,之后他也对自己的犯罪行为供认不讳。从这个案件中可以看到,对惊讶事件的察觉和发现,为警方寻找破案的突破口提供了重要的线索指引,这表明在刑事侦查工作中惊讶事件具有重要的证据力。
其次,当今社会比较流行的科学证据,如测谎证据、指纹证据和DNA证据,其证据力也会依赖于惊讶事件的证明力,因为这些证据都是通过严厉测试得到。严厉测试与惊讶事件具有非常紧密的联系,通过某种严厉测试就是一个惊讶事件;而惊讶事件的主要表现形式之一则是通过严厉测试。
在案件侦查活动中,许多侦查手段本质上就是一种严厉测试,如测谎、指纹识别和DNA鉴定,甚至被法律禁止的“刑讯逼供”也是一种严厉测试。如果一个理论或假说T通过了某些严厉测试,则这个结果是令人惊讶的,于是它将获得人们更多的支持和信任。对一个理论或假说T进行严厉测试,是指对T中某一先前被认为是非常可能错误的断言进行真假判断。也就是说,严厉测试是指主观上理论或假说T不可能通过的测试。
例如,测谎就是一种严厉测试。测谎仪的机理在于通过测定被测试者的呼吸、脉搏、血压、瞳孔、皮肤电、脑电波等参数,并将该参数与正常值(所谓的“讲真话”时的参数)相比较,得出被测试者的测试参数是否处于正常值的范围,从而确定被测试者是否说谎。耶鲁大学法学院乔恩·R·华尔兹(Jon.R.Waltz)教授在《刑事证据大全》一书中指出:统计数字表明,测谎检查的准确率一般在90%左右。可以设想一下,在科学技术高度发达、测谎仪检测参数设计得足够合理的背景下,测谎检查的准确率还将大大提高,这样说谎者几乎不可能通过测谎检查。有学者认为:测谎是对人精神的“刑讯逼供”,是测试者与被测者之间的精神较量,测谎专家利用数据、指标,使犯罪嫌疑人经历一场“精神浩劫”。所以,测谎就是一种严厉测试。对嫌疑人进行测谎检查,实际上就是对假说“此人没有说谎,他与案件无关”进行严厉测试。如果嫌疑人通过了测试,那么这个结果是令人惊讶的,因为说谎者几乎不可能通过测试,这样我们就有足够的理由相信假说“此人没有说谎,他与案件无关”为真。因此,可以断言:利用精密测谎仪对嫌疑人进行测谎检查,实际上是一种严厉测试,具有重要的证据参考价值。类似的,我们还可以断言,在案件侦破中广泛应用的“指纹识别”和“DNA鉴定”技术都应该是一种严厉测试,并且测试的结果将为筛选嫌疑对象、提高破案效率提供重要的指导意义。
四、结语
惊讶事件不仅在法律的刑事侦查中而且在科学发现中都具有重要的证据价值,但我们这里仅讨论了其法律证据学意义。霍里奇利用主观概率定量地对惊讶事件的描述尽管受到了哈克尔的挑战,但从法律证据学角度来讲,我们认为霍里奇惊讶事件的定义比哈克尔的更合理、更恰当,因为我们根据霍里奇定义并结合贝叶斯公式就可以判断在一定的背景环境下哪些经验陈述是令人惊讶的,也就是哪些为惊讶事件。惊讶事件的证据力表现为:如果一个理论或假说能精确地预测或解释惊讶事件,那它将获得人们更强的支持和信任,因为惊讶事件是小概率事件,它和一个理论或假说的确证度成反比关系,即惊讶事件的概率越小,则预测该惊讶事件的理论为真的可能性越高。同时,从科学逻辑角度来讲,惊讶事件是严厉测试的一种表现结果,反过来讲,严厉测试可以产生惊讶事件。这一点在案件侦查和法庭审判等司法活动中都表现得更加明显。在司法过程中,如果充分利用惊讶事件的证据力,那就可以大大降低错案发生的概率,从而为通达司法公正、维系法律理性和建设法治中国提供方法支援。
[致谢]本文还得到了华东政法大学校级项目(12HZK005)资助,特此致谢!
[1]爱因斯坦.爱因斯坦文集:第一卷[M].许良英,等,译.北京:商务印书馆,1976.
[2]Copi Irving M.,Burgess-Jackson K.Informal Logic:3rd edition[M].New Jersey:Prentice Hall,1996.
[3]Achinstein P.The Concept of Evidence[M].New York:Oxford University Press,1983.
[4]Popper K.The Logic of Scientific Discovery[M].New York:Routledge,2004.
[5]Horwich P.Probability and Evidence[M].Cambridge:Cambridge University Press,1982.
[6]Manson N A.,Thrush M J.Fine-Tuning,Multiple Universes,and The“This Universe”Objection[J].Pacific Philosophical Quarterly,2003,(1).
[7]Olsson E.Corroborating Testimony,Probability and Surprise[J].British Journal for the Philosophy of Science,2002,(2).
[8]White R.Fine-Tuning and Multiple Universes[J].Noûs,2000,(2).
[9]Harker D.A Surprise for Horwich(and Some Advocates of The Fine-Tuning Argument(Which Does Not Include Horwich(As Far As I Know)))[J].Philosophical Studies,2012,(2).
