动态VaR约束下Stein-Stein波动的保险最优决策

孙宗岐，刘宣会

（1.西安思源学院高数教研室，陕西 西安710038；2.西安工程大学理学院，陕西 西安710048）

0 引言

近几年，对投资组合选择问题的研究已经很丰富，但大多数研究都集中在个人投资主体领域，而对保险资金的投资组合问题相对较少.虽然两者理论框架大致一致，但研究保险资金的投资组合问题有其不容忽视的特殊意义.我国从2005年开始对保险资金进入资本市场逐步开放，保障保险资金的良性运作由此显得十分重要，目前国内在这方面的研究已经起步.郭文旌［1］在风险证券价格服从跳-扩散过程假设下，利用均值-方差准则通过使用最优控制原理研究了保险公司的最优投资问题.张言林［2］等采用动态规划原理研究了最大化投资期间消费效用的带实业项目的投资组合问题.陈树敏［3］等在保险公司盈余服从扩散过程的假设下，应用混合随机控制-最优停时方法，研究了最小破产概率下保险资金投资于资本市场和实业项目时最优投资组合问题.在这些文献中，普遍假设方差为常数或确定性函数，然而研究表明，风险资产的波动率是随机的［4-8］.作为一种双侧风险，方差常常把高收益的部分划为风险加以限制，这显然有悖于投资者的初衷.VaR方法作为一种下侧风险近年来深受研究者的青睐，已有学者引入到保险资金的管理研究中，如郭文旌等［9］以VaR度量保险公司的整体风险，利用均值-VaR模型研究了保险公司的投资策略选择问题；王海燕等［10］研究了保险公司再保险一投资问题在均值-方差（M-V）模型和均值-在险价值（M-VaR）模型下的最优常数再调整策略.但是他们都只度量了终端时刻的静态VaR风险，没有度量整个投资过程的动态VaR风险.陈树敏，李仲飞［11-12］考虑了动态VaR风险约束下的保险投资决策问题，但是没有对风险资产的波动率做随机假设，这显然和资本价格的随机波动性不符.到目前为止，国内在动态VaR约束下考虑具有随机波动率风险的保险公司最优投资组合问题较少，本文中将采用Stein-Stein模型来度量随机波动率，同时考虑受动态VaR约束的保险公司最优投资决策问题，在最小破产概率准则下，运用随机最优控制原理和库恩-塔克条件得到最优金融决策的显式解.

1 建立模型

1.1 模型描述 刻画保险公司盈余水平的经典模型是Cramer-Lundberg过程其中x0是初始盈余，p是保费率表示保险公司到t时刻为止的累积索赔，其中Yi表示第i次发生的索赔额，Yi独立同分布，假设Yi服从参数为的指数分布，N（t）是参数为λ的泊松过程，表示到时刻t为止发生的索赔次数.为了安全起见，保费率需满足p＝（1＋γ）λα，γ＞0称为相对安全负荷.

根据Taksar［13］的研究，保险公司的盈余水平R（t）可近似地用扩散过程

其中r是无风险利率，波动率V（t）满足Ornstein-Uhlenbeck（OU）过程，即

即

亦即

为了能对模型经行严格数学描述，假定上述所有随机变量和过程都定义在完备概率空间（Ω，F，P）上，且产生的σ信息流为｛Ft：t＞0｝.设P是R0＝x下的条件概率，所有平方可积且Ft适应的策略π的集合为可行集Π.定义破产时刻

根据VaR的定义，对于给定置信水平α，

其中N-1（α）是标准正态分布的分位数，x＋＝max｛0，x｝.

2 求解模型

我们的目的是在t≥0时，求解下列最优控制问题

2.1 动态VaR控制的等价条件

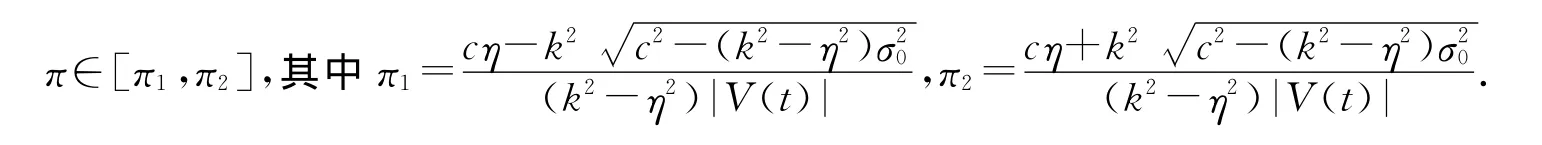
命题1的证明

即

进而动态 VaR约束等价于π∈［π1，π2］.

即

根据 Lundberg等式［15］，不妨假设 HJB方程有形如ψ（t，x，V（t））＝e-β［a（t）x＋（v（t）-θ）］，a（t）＞0形式的解，则ψt＝e-β［a（t）x＋（v-θ）］［-βxa′（t）］，ψx＝e-β［a（t）x＋（v-θ）］［-βa（t）］，ψV＝e-β［a（t）x＋（v-θ）］（-β），ψxx＝e-β［a（t）x＋（v-θ）］［-βa（t）］2，ψVV＝e-β［a（t）x＋（v-θ）］（-β）2，ψxV＝e-β［a（t）x＋（v-θ）］［-βa（t）］（-β）.显然满足ψx＜0，ψxx≥0，且ψ（t，x，L）∈C1，2，2（R＋×R＋×R＋）.

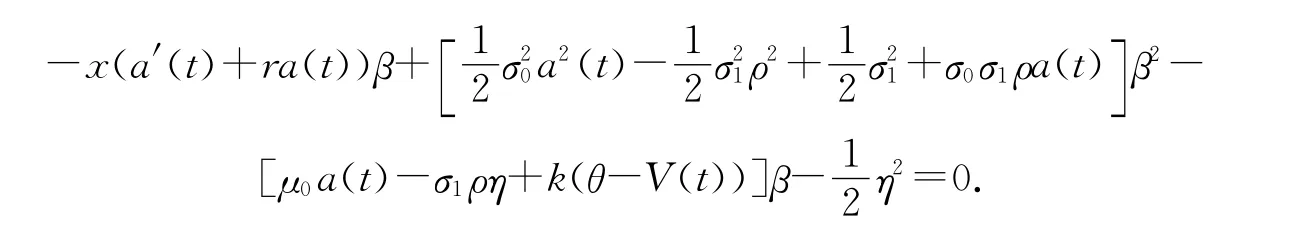
上式消去对x的依赖可得两个方程a′（t）＋ra（t）＝0，a（0）＝1和

容易解第一个方程得a（t）＝e-rt.

下面解第二个方程，显然

2.3 受动态VaR约束的最优投资策略及最小破产概率的显式解定理1 在动态VaR约束下，最优化问题（2）的最优投资策略为

最优化问题（2）的最小破产概率为

定理1的证明 当V（t）≠0时，优化问题（2）作为不等约束的非线性规划我们可建立如下随机Lagrange函数［16］

由一阶最优性条件有

进而

若λ＝0，则

若其满足不等式约束条件，即动态VaR约束条件，则其是最优投资策略，此时说明动态VaR约束与无约束时一致.如果其不满足VaR约束，即πt＊＜π1或者πt＊＞π2，当时，显然因此先讨论将代入（3）式，注意到ψxx＞0，有所以λ≥0，即π1是K-T（库恩-塔克）点.又由于该问题是凸规划问题，所

以π＊＝π1.

注意到当a（t）＝1，V（t）＝θ时，即破产概率与时间无关，并且资产价格波动率是确定常数时，就是林祥［15］研究的破产概率，因此文章也扩展了林祥的最小破产概率公式.

3 结语

在保险公司盈余服从扩散过程的假设下，考虑具有随机波动率的保险公司最优投资决策问题.在动态VaR约束下，使用动态规划原理建立了最优投资选择模型，在最小化破产概率准则下通过求解HJB方程和运用库恩-塔克条件得到了最优投资决策和最小破产概率的显示解.结果对于保险公司的管理具有一定的现实指导意义，同时对金融数学中的保险资金的投资消费选择问题也具有一定的理论价值.

［1］郭文旌，赵成国，袁建辉.跳扩散市场的最优保险投资决策［J］.系统工程理论与实践，2011，31（4）：749-760.

［2］张言林.投资于实业项目且借款利率高于存款利率时的投资组合优化问题［D］.济南：山东大学金融研究院，2005.

［3］陈树敏，李仲飞.保险公司实业项目投资策略研究［J］.系统科学与数学，2010，30（10）：1293-1303.

［4］Heston S L.A closed-form solution for options with stochastic volatility with applications to bond and currency options［J］.Review of Financial Studies，1993：327-34.

［5］Stein E M，Stein J C.Stock price distributions with stochastic volatility：an analytic approach［J］.Review of financial Studies，1991（4）：725-752.

［6］Hull J，White A.Pricing interest-rate derivative securities［J］.The Review of Financial Studies，1990（3）：573-592.

［7］Hull J，White A.One factor interest rate models and the valuation of interest rate derivative securities［J］.Journal of Financial and Quantitative Analysis，1992，28：235-254.

［8］吴鑫育，马超群，汪寿阳.随机波动率模型的参数估计及对中国股市的实证［J］.系统工程理论与实践，2014，34（1）：35-44.

［9］郭文旌，李心丹.VaR限制下的最优保险投资策略选择［J］.系统管理学报，2009，18（5）：583-587.

［10］王海燕，彭大衡.再保险一投资的 M-V及 M-VaR最优策略［J］.经济数学，2011，28（3）：72-76.

［11］Chen S M，Li Z F.Optimal investment-reinsurance policy for an insurance company with VaR Constraint［J］.Insurance：Mathematics and Economics，2010，47：144-153.

［12］陈树敏.保险公司风险控制与投资策略研究［D］.广州：中山大学数学与计算机科学学院，2010.

［13］Taksar M，Markussen C.Optimal dynamic reinsurance policies for large insurance portfolios［J］.Finance and Stochastic，2003（7）：97-121.

［14］Krylov R.Controlled diffusion process［M］.New York：Spring-Verlag，1980：24-25.

［15］林祥，钱艺平.跳-扩散风险模型的最优投资策略和破产概率研究［J］.经济数学，2009，26（2）：1-8.

［16］刘宣会，赵宁宁，续秋霞.基于随机LQ控制的套期保值策略研究［J］.系统工程理论与实践，2010，30（6）：1034-1039.