关键路径的矩阵计算公式
2014-08-20朱志雄
朱志雄
(武汉软件工程职业学院人文学院,湖北 武汉430205)
0 引言
计划评审方法(program evaluation and review technique,PERT)和关键路线法critical path method,CPM)广泛地用于系统分析和项目管理,是20世纪50年代由美国的两个不同公司、机构分别提出并发展起来的.由于PERT与CPM有着相同的目标应用,由有很多相同的术语,这两种方法常被合并为一种方法,称为PERT/CPM,也称为求关键路径法.PERT/CPM是一种基于数学计算的项目计划管理方法.它是将整个工程项目分解成为多个独立的活动并确定每个活动的工期,按工期完成的前后逻辑顺序将活动连接成一个有向赋权图——AOE网(activity on edge),从而能够计算项目的工期、各个活动时间特点(最早、最晚时间、时差)等.并从中分析影响整个工程项目中关键项目的路径、时间长度及缓冲时间等.
关键路径法的计算原理大致相同,主要用于大型项目管理,由于软件工具的先进性,人们的关注点主要集中在软件程序设计的实现[1-2]以及计算程序在时间复杂度(数量级)上[3-4].而关注从原理自身出发的数学公式化研究的人不多[5].从原理上看,它是有向赋权图的分析、计算,而有向赋权图的数学计算是基于其矩阵运算.笔者试图从原理出发,给出有向赋权图的矩阵表示,并相应地定义其矩阵的运算,由此推导出关键路径法最简单的数学表达式(矩阵计算公式).它是受最短通路研究[6]的启发,利用“对偶性”,将计算最短通路方法中著名的Dijkstra算法[7-8]“移植”于关键路径法上.
所谓“对偶”,是因为在赋权图中,求最短通路问题与最长通路问题—PERT/CPM图中的关键路径问题互为“对偶”问题.由此,定义“对偶”的邻接矩阵,并借助于最短通路邻接矩阵算法中“加法”(取小)运算的思路,定义有向图简单赋权图邻接矩阵以及其相应的“乘法”(取大)运算,并巧妙利用“乘法”运算中零元、单位元的运算性质,从而得出PERT/CPM图关键路径的矩阵计算公式,推导关键路径的矩阵计算公式,其现实意义在于,其一数学公式表达简单直观,从而体现数学抽象化之美感、数学表达式之精辟扼要;其二让更多的人从原理上,通过简单易行的数学公式掌握关键路径的计算方法,以达普及运用之目的.
1 有向简单赋权图邻接矩阵定义
在研究最短通路时,定义了有向赋权图的邻接矩阵及其算法[6].在此基础上,根据对偶性,不难定义PERT/CPM图的邻接矩阵.在求最短通路问题中,不相邻的顶点间的“权”定义为“∞”;在求最长通路问题(PERT/CPM)中,不相邻的顶点间的“权”定义为“0”[9].
定义1 设简单有向赋权图D=〈V,E,W〉,其中V,E,W分别是图D的点集、边集及边对应的权的集合,|V|=n,在D上定义一个n阶矩阵A=(aij)n×n.

其中1)eij∈E为V中顶点vi与顶点vj之间的边,wij∈W为eij对应的权;
2)若顶点vi与顶点vj之间不存在边,则令aij=0(“乘法”运算中的零元)[9];
3)特别地,若顶点vi与顶点vj之间存在边eij,且wij=0,则令aij=e(e为“乘法”运算中的单位元);
4)并规定aii=e;
则称矩阵A=(aij)n×n为D的赋权邻接矩阵.
2 有向简单赋权图邻接矩阵的“乘法”运算定义
在最短通路中我们定义了矩阵的“加法”运算.在研究最长通路时,由对偶性,不妨定义赋权简单有向图的矩阵的“乘法”运算.(对偶性:“加法”运算⊕取小运算[6];“乘法”运算⊗用取大运算定义).根据乘法运算中的零元和单位元运算法则,给出以下矩阵乘法的定义:
定义2 设A=(aij)n×n,B=(bij)n×n是两个n阶矩阵,定义矩阵C=(cij)n×n为矩阵A与B的“乘法”⊗
运算,即C=A⊗B,其中cij=max{ai1⊗b1j,ai2⊗b2j,…,ain⊗bnj}.
定义:当aik≠0,bkj≠0时,aik⊗bkj=aik+bkj;
并且有:aij⊗0=0⊗aij=0;aij⊗e=e⊗aij=aij.
3 PERT/CPM图的定义与性质
定义3 设简单有向赋权图D=〈V,E,W〉为PERT/CPM图,其中|V|=n.根据PERT/CPM图的定义和性质,对顶点vi下标作如下顺序标注规定:
1)v1是发点,vn是收点[10];
2)如果i<j,边(vi,vj)=eij存在,其权为wij=aij,其中aij≥0,若wij=0,则令aij=e;
3)如果i>j,(vi,vj)=eij不存在,令其权wij=aij=0;
4)如果i=j,则wii=e.
由定义1、2、3以及PERT/CPM图的定义,可得以下性质:性质1 1)PERT/CPM图的邻接矩阵A为上三角形矩阵;
2)其转置矩阵AT对应的图形也是PERT/CPM图,其邻接矩阵为下三角形矩阵,它是原图的反向PERT/CPM 图,vn是发点,v0是收点.
设PERT/CPM图对应的赋权邻接矩阵A,记A2=A⊗A,A3=A2⊗A,…,An-1=An-2⊗A.性质2 设a(k)ij,a(k-1)ij分别是Ak,Ak-1(k=2,3,…,n)中第i行j列的元素,则必有:a(k)ij≥a(k-1)ij.所以时,因为所以,当l=k时,由Ak=Ak-1⊗A,可得
性质3 由定义2及A⊗A=A2,因为
性质2的证明l=2时,由矩阵乘法的定义所以是顶点vi到顶点vj通路中,通路长度不超过2的最长通路的权,
同理,在A3中是顶点vi到顶点vj通路中,通路长度不超过3的最长通路的权.
在Ak中是顶点vi到顶点vj通路中,通路长度不超过k的最长通路的权.
4 PERT/CPM图关键路径求解的矩阵计算公式
定理1 设有向简单赋权图D=〈V,E,W〉为符合定义3的PERT/CPM图,|V|=n,A=(aij)是D的n阶邻接矩阵.令A2=A⊗A,A3=A⊗A⊗A=A2⊗A,……,An-1=An-2⊗A.一定存在1≤k≤n-1,使得Ak=Ak⊗A=Ak+1.
在矩阵A=(aij)中,如果则相应的通路v1→vi→vj→vk→…vm→vn是图D的关键路径.
注:D的转置矩阵AT是图D的反向PERT/CPM图,其“乘法”可以得到图D的反向图的关键路径,其通路与图D的相反,即vn→vm→…vk→vj→vi→v1也为其关键路径.
5 PERT/CPM图中关键路径的求法
求关键路径的方法是,通过计算PERT/CPM图中从发点v1到收点为vi(i=1,2…,n)的最早完成时间和最晚完成时间[10],导出v1到vn的关键路径.
6 例题
例题:求在题图1中顶点v1到顶点v2,v3,…,v7的最早完成时间和顶点v1到顶点v7的关键路径[10].
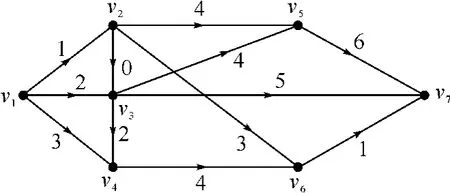
图1 PERT/EPM图
解:由题图得,赋权邻接矩阵为:

所以,A4=A3.
由定理1及矩阵A3可得:v1到v7的最早完成时间为12.在邻接矩阵A中,由于a13+a35+a57=2+4+6=12=a(3)17.所以,图D的关键路径为:v1→v3→v5→v7.
具体求关键路径步骤为:
1)顶点v1到顶点v1,…,v7的最早完成时间分别为e,1,2,4,6,8,12.(A3中第一行的各元素);
2)顶点v1,…,v7到顶点v7的最早完成时间分别为12,10,10,5,6,1,e.(A3中最后一列的各元素);
3)l1i=为顶点v1到顶点vi(i=1,2,…,7)从发点v1到收点v7路径中的的最晚完成时间,分别为,e,2,2,7,6,11,12;
4)对照比较顶点v1到顶点v1,…,v7的最早完成时间a(3)1i与最晚完成时间li(i=1,2,…,7),可得所以,顶点v1,v3,v5,v7是关键点,它们的连线v1→v3→v5→v7就是关键路径.而顶点v2,v4,v6为缓冲点.顶点v2的缓冲时间为顶点v4的缓冲时间为顶点v6的缓冲时间为
7 结束语
用赋权图邻接矩阵的新定义及相对应的矩阵“加法[6]”、“乘法”运算的定义,对最短通路与PERT/CPM图关键路径(即最长通路)问题进行研究的意义在于:有利于把最短通路和PERT/CPM图关键路径问题中复杂的计算公式用简单明了的矩阵运算公式表达;有助于我们用赋权图的邻接矩阵及两种新运算对其他赋权图问题的研究;由此也可以对赋权图矩阵的“加法”、“乘法”运算的代数结构等做进一步的研究.
[1]徐凤生.一种新的关键路径求解算法[J].计算机应用与软件,2005(6):97-99.
[2]郭黎斌.关键路径算法的实现[J].机械管理开发,2006(10):77-79.
[3]白青海.几种求关键路径算法的分析[J].内蒙古民族大学学报,2008(2):134-137.
[4]王明福.一种求解关键路径的新算法[J].计算机工程,2008(5):106-108.
[5]徐利民.关键路径的矩阵算法[J].淮南职业技术学院学报,2001(1):100-102.
[6]朱志雄,杨树清.无向赋权图最短通路的矩阵算法[J].湖北工业大学学报,2012(5):106-108.
[7]Kenneth H.Rosen.离散数学及其应用[M].袁崇义,屈婉玲,王贪,译.北京:机械工业出版社,2002:475-477.
[8]John A.Dossey,等.离散数学[M].章炯民译.北京:机械工业出版社,2007:132-133.
[9]司守奎,孙玺菁.数学建模算法与应用[M].北京:国防工业出版社,2013:38.
[10]任现淼.计算机数学基础(上)[M].北京:北京中央广播电视大学出版社,2000:182-183.
[11]邵学才,蒋强荣,等.离散数学[M].2版.北京:机械工业出版社,2007:98.
