考虑极限倾覆失效的混凝土坝整体稳定状况分析

，，，

(1.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，南京 210029；

2.河海大学 水利水电学院,南京 210098)

1 研究背景

在结构设计和安全状况分析时须综合考虑承载能力极限状态和正常使用极限状态。以往分析中，多将2种失效状态混合考虑，这种方法不便于各种安全状况的分级分档。基于失效机理的结构安全状况细化分析能更好地反映实际，使结构安全评价更合理。混凝土坝安全计算分析中通常考虑滑移、坝踵拉裂和坝趾压碎应力超限3类失效模式[1]。应力超限本身并不是一种整体极限失效模式，而是一种正常使用极限状态；局部压缩、拉裂或剪切破坏并不会直接导致整体失效，但可能是整体失效的致因[2]。更严格地说，整体失效模式是多个局部应力超限失效模式的并联事件。将应力超过承载能力作为一种失效状态，不允许坝踵拉裂和坝址压碎，是因为并未考虑极限倾覆(Limit overturning)这一极限失效状态。本文重点研究混凝土坝整体失效极限状态，所指整体失效是坝体和基岩构成的整个系统不能满足设计规定的功能要求。

依据坝高为30～170 m建于1912—1974年间17座不同基岩类型的钻孔样本的试验数据，EPRI(Electric Power Research Institute)统计得到重力坝坝体混凝土-基岩胶结面的抗拉强度，平均抗拉强度为0.8 MPa，大约为坝体混凝土强度的50%[3]。Fishman进行了大量室内和现场试验(如Kurpsay坝、Krapivino坝和Tashkumir坝)，试验结果表明混凝土-基岩胶结面并不一定是应力超限的最薄弱区域，当有效粘结时，胶结面强度的存在使得失效往往发生在相对强度较低的基岩内；同时，试验还表明，即使基岩变形模量较低，仍可能存在较高的抗剪强度[4-5]。这些研究成果都表明，欲更加准确地辨识混凝土坝的安全状况，需要将坝基、坝体及其胶结面视为一个系统考虑，以识别其整体失效模式[6-9]。

事实上，若基岩不存在软弱面且相对坝体强度较低时，混凝土坝既不会发生滑移失稳也不会发生倾覆失效；但可能发生坝体-基岩整体极限倾覆失效。极限倾覆失效的起始阶段即产生拉伸裂缝在实际混凝土坝工程中并不少见(如Malpasset坝、Austin坝、Bratsk坝和Schlegeis坝等)，向基岩扩展的拉伸裂缝导致坝基扬压力显著增大，灌浆帷幕断裂，进而引起渗流量增大、排水孔和测压孔喷水等。以往设计分析时，经常忽视极限倾覆失效，以Malpasset坝为例，设计时充分考虑了基岩剪切失稳问题而忽视了基岩的低抗拉和抗压性，最终因极限倾覆失稳造成严重后果。为此，一些国家(如俄罗斯)的标准规范已经将极限倾覆失效纳入设计标准规范中。

本文在现有研究的基础上，以重力坝为例，探索研究了基岩上混凝土坝的极限倾覆失效模式，推导了极限倾覆失效模式的状态函数，进而建立了重力坝失效模式的通用模型，在此基础上，以一在役工程为例，计算比较了抗滑失稳和极限倾覆2种整体失效状态，结合坝体-胶结面-基岩系统的非线性数值分析结果，表明了重力坝整体稳定分析时考虑极限倾覆失效模式的重要性。

2 重力坝系统的极限倾覆失效

2.1 极限倾覆失效的初步分析

对于粘结良好的混凝土-基岩胶结面，坝体-基岩系统的失效模式比较复杂，普遍认可将最先在加载端的奇异点处(如坝踵处)产生拉裂缝并扩展，而对最终失效不同学者则有不同的看法。部分学者认为系统最终会因基础剪切破坏而失效；部分学者假定基岩是完整的，对坝体、坝基和胶结面分别采用相应的合理的本构模型，通过数值分析认为，重力坝一般有3条主要破坏模式[4-5, 10-11]：1条在基岩内发展，1条在坝体内发展，这2条的起始点都在坝踵处；第3条则是坝体与基岩的胶结面。重力坝既受到自重引起的压力又受到水荷载等引起的剪切力，当坝体或基岩强度不足，就可能引起拉裂或压碎。对于相对较软弱的基岩，Fishman通过多座重力坝的现场试验同样发现，在失效的最后阶段会在块体受剪荷载的另一端基础内(如坝趾处)的受压区会产生不连续面，并伴随着明显的旋转。上游面基岩拉裂和下游面基岩压裂过程中，坝基防渗和排水系统失效，扬压力增大，进一步加剧了极限倾覆失效。重力坝的系统失效与基岩性质有很大关系，当基岩性质较差时，破坏主要可能发生在坝基内[4-5, 10-11]。

ICOLD的1995年公报总结了混凝土坝失事的主要原因，其中坝基问题是最主要原因，侵蚀和强度不足分别占失事原因的21%[12]。以坝趾的相关点为矩心，如果自重抗力力矩小于倾覆力力矩，将发生极限倾覆失效。除此之外，根据基岩极限承载能力准则，如果在上游坝踵产生拉伸裂缝，将导致坝体-基岩胶结面扬压力过大，故要确保抗倾覆稳定，还需要将坝体受到的合力控制在胶结面中心的3/5范围内。类似极限承载能力极限状态，这一控制准则也不是真正意义的极限状态准则。

2.2 基础抗压合力的计算

极限倾覆状态的稳定系数可以定义为

Fs=ΣMr/ΣMs。

(1)

式中：ΣMr和ΣMs分别是抗力和倾覆力相对图1中O转轴点的力矩总和。

图1 混凝土重力坝倾覆模式受力示意图

分别计算图1中各外力的力矩，ΣMr包括结构自重G、基岩抗压抗力S和下游静水压力Wd的力矩；ΣMt则包括上游静水压力Wu、泥沙压力E、扬压力U和地震力Peq。O轴由以下两式确定：

a=N/tRcr;

(2)

d=(h2+2ae-a2)1/2-h。

(3)

式中：Rcr是坝基的抗压抗力；N和T分别是外力的垂直和水平方向分量的合力；h和e分别是T和N对下游坝趾B的力臂；t是坝段的宽度。从而可得基岩抗压抗力为

S=(a2+d2)1/2tRcr。

(4)

2.3 坝基抗压抗力测试确定

对基础抗压抗力，可以通过室内或现场试验的方法测试得到。试验模型如图2所示，给模型施加二维荷载即法向荷载N和剪切荷载T。

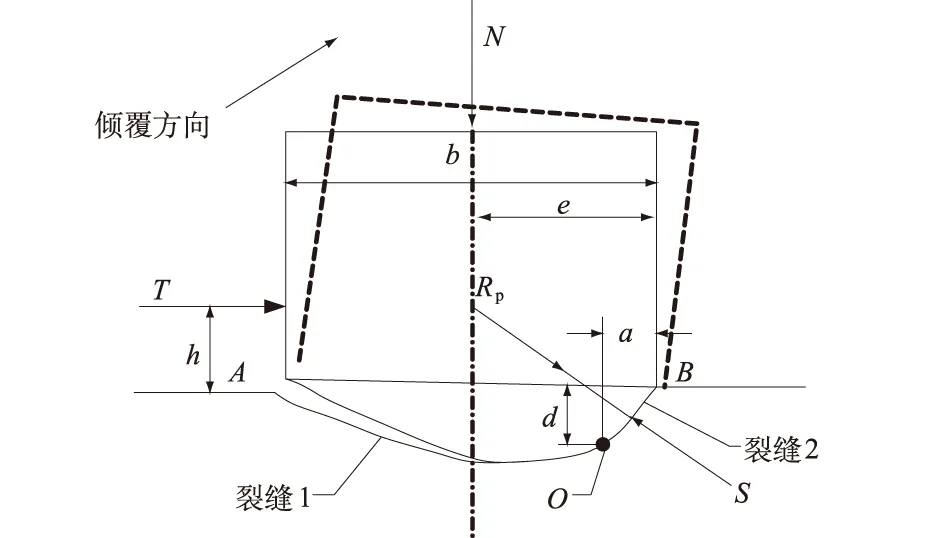
图2 岩基上混凝土结构失效连续模型

由静力平衡(ΣX=0;ΣY=0)和力矩平衡(ΣM=0)方程得到极限剪切荷载为

Tp=[(htRcr)2+2NetRcr-N2]1/2-htRcr。

(5)

相应地，剪切面的极限剪切应力为

(6)

由式(5)和式(6)可以得到抗压抗力

(7)

上述公式中：τp=Tp/A,τp可通过试验计算得到;σn=N/A;A=bt；A为基底面面积；t为坝体厚度;m和n分别为荷载N和T的偏心率，即m=0.5-e/b,n=h/b。

基础抗压抗力Rcr也根据下式由基岩弹性模量Er估算[6]：

Rcr=13×10-4Er。

(8)

3 重力坝系统的整体失稳模式和状态函数

考虑极限倾覆失效，建立如图3所示的混凝土重力坝整体失稳模式体系。图中，沿胶结面(完整和损坏2种情况)失稳、基岩软弱面(完整和损坏2种情况)失稳以及倾覆失稳等失效模式分别记为Z1,Z2,Z3,Z4,Z5。

图3 混凝土坝系统失稳模型

混凝土-基岩胶结面表现为脆性，在较小的相对位移下即可能失效。失效前胶结面的剪切抗力可以用M-C失效准则描述；而当胶结面损坏或者部分损坏时，剪切抗力则由内摩擦角和剪胀角确定。按胶结面是否完好对沿混凝土-基岩胶结面的抗滑稳定极限状态分别定义。

当胶结面完好或者部分完好时(图4(a)至图4(d))的极限状态函数为

Z1=cAc+N′Rtanφi-T。

(9)

式中：Ac为有黏聚力c的胶结面面积；N′为有效法向荷载；R为法向应力作用在Ac的比例；φi为内摩擦角；T为平行胶结面的荷载。

胶结面破坏时(图4 (e))的极限状态函数为

Z2=N′tan(φb+i)-T。

(10)

式中：φb为基本摩擦角；i是粗糙峰引起的剪胀角。

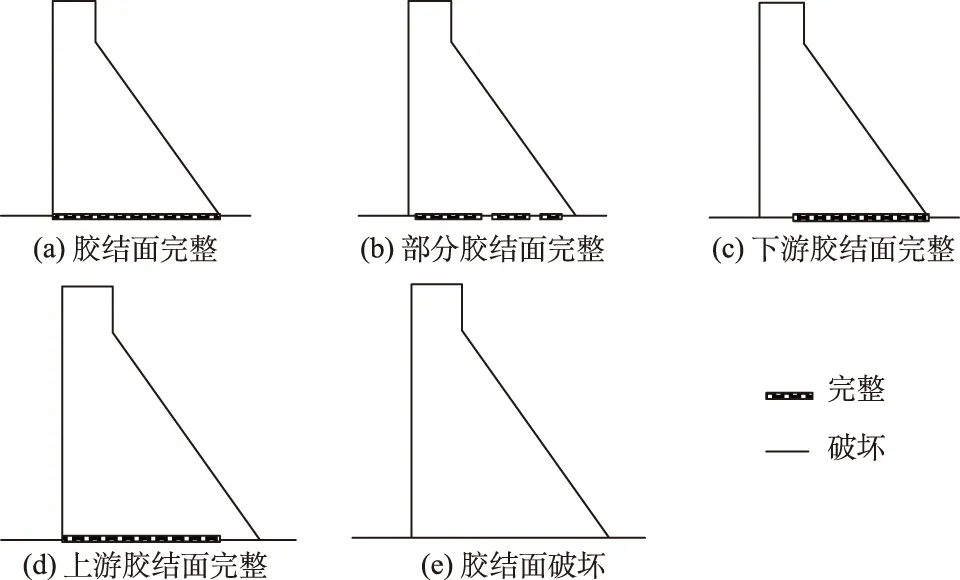
图4 混凝土-基岩胶结面状况

当极限状态Z1发生后，只有当极限状态Z2也发生，坝体才会沿基础面滑动，也就是，极限状态Z1和Z2是平行的系统，如图3。

沿基岩软弱面或节理的滑动受节理面抗压强度、表面粗糙度、风化程度和填充物类型影响。类似地，基岩内的滑动同样有2个极限状态函数，且2种极限状态也为平行的系统。当滑动面完整时，

Z3=cmAm+N′tanφm-T。

(11)

式中：cm和φm分别为基岩的黏聚力和内摩擦角；Am为潜在滑移路线上的完整基岩的面积。

沿节理的滑动极限状态函数则为

Z4=N′tan(φbj+ij)-T。

(12)

式中φbj和ij分别为节理的基本摩擦角和剪胀角。

坝体应力可由Navier公式计算得到，即σ=(V/A)±(Mcytp/I)，其中，V为竖向荷载，Mc为过胶结面中心轴的力矩；ytp为计算点距质心的距离，I为惯性矩。如前所述，应力超限是整体失效的诱发因素，而不作极限状态考虑。将极限承载力状态包含在倾覆失效模式中，极限状态函数为

(13)

4 工程实例分析

4.1 工程概况

某在役水电站拦河大坝为1级水工建筑物。水库正常蓄水位173 m，坝顶高程179.00 m，设计、校核洪水位分别为174.76(洪水重现期为0.2%)、177.80 m(洪水重现期为0.02%)，下游水位基本稳定，属不完全调节水库。典型挡水坝段截面如图5，坝顶宽度7.0 m，坝底高程80.0 m，坝底宽度73 m，坝基面水平。

图5 典型纵向剖面示意图

坝体的综合弹性模量为27.71 GPa，泊松比ν=0.189。岩石-岩石抗剪断强度为tanφbj=1.4，cm=2.5 MPa。坝基微风化花岗岩弹性模量为1.25×104MPa，泊松比ν=0.2。混凝土-基岩胶结面的摩擦系数和黏聚力，抗剪断强度建议值tanφi=1.15，c=1.2 MPa；有关抗拉强度的信息较少，这里根据脆性材料断裂的Griffith理论中有关抗拉强度σt和黏聚力c的关系c=2σt近似得到胶结面的抗拉强度。

基于实测数据，坝体上游水位均值H=93.0 m；运行初期的实测扬压力折减系数α为0.341。

4.2 整体稳定状况分析

4.2.1 极限倾覆失效模式分析

上游面基岩拉裂和下游面基岩压裂导致坝基防渗和排水系统失效，假定拉裂破裂面上的扬压力从上游到下游呈直线下降。依据图1所示受力图，只考虑静水压力工况，计算作用在单宽横剖面(图5)上的荷载(106N)：坝体自重G=3.579γc、上游水压力Wu=0.005H2。两者对下游坝趾B点的力臂分别为：eG=48.9 m和eH=31 m。根据下文中混凝土坝系统应力的数值分析结果，确定基岩上游坝踵以下拉应力和下游坝趾以下压应力的主应力面，由此可得扬压力U=32.53，eU=49.76。竖向合力力臂e=48.38 m，水平向合力力臂h=27.78 m。

由式(2)和式(4)，代入参数，可确定O轴的坐标：

a=N/tRcr=53.49/16.25=3.29(m);

d=(h2+2ae-a2)1/2-h=

(27.782+2×3.79×48.38-

3.29×3.29)1/2-27.78=5.07(m)。

压碎面OB的长度为

bcr=(a2+d2)1/2=(3.292+5.072)1/2=6.04(m)。

抗压碎峰值力为

S=Rcrbcrt=16.25×6.04×1=98.21×106(N)。

相对O轴坝体倾覆的抗力矩和为

ΣMr=G(eG-a)+0.5Sbcr=G(48.9-3.29)+

0.5×6.042×Rcr=42 141.13(MN·m)。

相对O轴坝体倾覆的力矩和为

ΣMs=Wu(eH+d)+Uv(eUv-a)+Uh(d-eUh)=

Wu(33.1+5.07)+Uv(49.76-3.29)+

Uh(5.07-1.69)=2 532.71(MN·m)。

其中Uv，Uh分别表示垂直向、水平向的扬压力分量。从而可得极限倾覆的安全系数为

Fs=ΣMr/ΣMs=4 214.13/2 532.71=1.66。

4.2.2 抗滑稳定失效模式分析

考虑到基岩完整，无明显的软弱面和断层，只需分析混凝土-基岩胶结面的抗滑稳定状况。胶结面的扬压力为Uc=(0.03+0.395α)H。由此，胶结面的抗滑稳定系数为

Fs=(cAc+N′tanφi)/T=

(73×1.2+72.24)/43.25=3.7。

4.2.3 对比分析

从以上分析可以看出，坝体极限倾覆的安全系数为1.83，小于沿混凝土-基岩胶结面抗滑稳定系数(即3.7)，从而该坝的整体失效模式应当考虑极限倾覆状况。

如前文所述，在数值分析过程中，如果分别采用不同的合理的坝体、胶结面和基岩本构模型，能够更加实际地模拟混凝土坝系统的实际工作性态，反映其最可能失效模式。采用与极限倾覆失效相同的参数，针对坝体混凝土、混凝土-基岩胶结面和基岩，分别采用混凝土损伤模型、水-力耦合模型(或Mohr-Coulomb弹塑性模型)和Drucker-Prager弹塑性模型等，通过非线性有限元分析判断大坝的安全性态。计算得到的x向(顺河向)主应力如图6所示，进一步分析表明，坝踵下方的基岩坝踵处出现一定的塑性应变，损伤参数为0.42。数值分析结果表明，当前状态下，混凝土坝系统工作正常，不会出现应力超限失效(小于达到破坏的损伤参数阈值)；但遭遇基岩老化和偶然突发荷载等工况时，混凝土坝系统失稳最可能从坝踵附近基岩拉裂开始，进而由于基岩的破坏和发展引起极限倾覆失效。

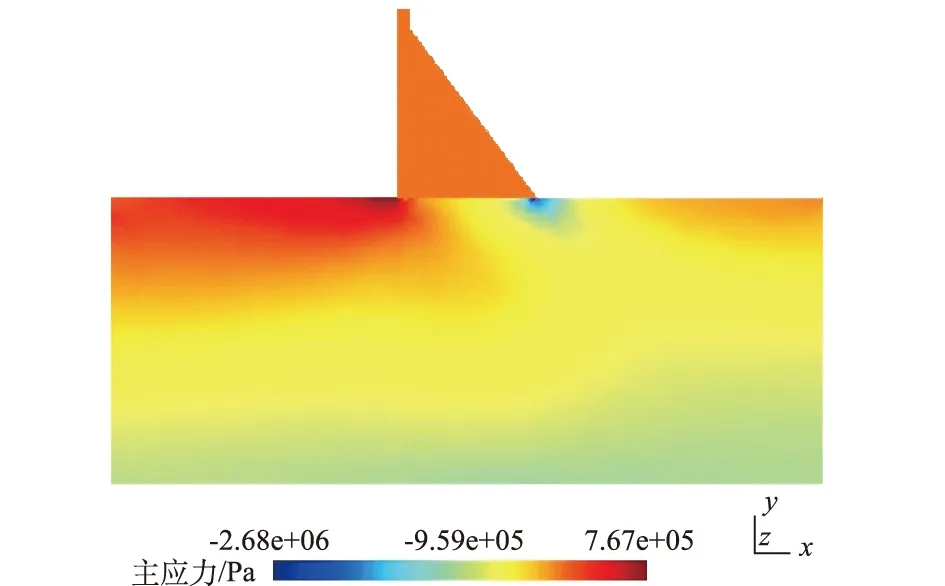
图6 x向(顺河向)主应力云图

以上分析说明，若混凝土-基岩胶结面两侧岩石与混凝土坚硬、强度高，基岩与混凝土成刚性接触，剪切破坏严格沿胶结面发生；若两侧岩石与混凝土软弱、完整性差，或一侧软弱，则除沿胶结面外，还可能局部或大部分甚至全部在软弱一侧基岩中发生破坏。

5 结 语

坝基问题是导致岩基上重力坝失效的主要成因，本文针对坝基为完整软弱基岩的情形，提出了因坝踵以下基岩拉裂、坝趾以下基岩压碎引起的极限倾覆失效模式，推导出极限状态函数；同时，提出了基岩基础抗压抗力测试方法。综合已有研究成果，考虑了重力坝系统失效的主要模式，构建了包含极限倾覆模式在内的重力坝失效模式串并联模型。通过某工程实例的分析，说明了在分析重力坝整体安全状态时考虑极限倾覆失效模式的重要性。

参考文献：

[1] SU Huai-zhi, WEN Zhi-ping, HU Jiang,etal. Evaluation Model for Service Life of Dam Based on Time-varying Risk Probability [J]. Science in China Series E: Technological Sciences, 2009, 52(7): 1966-1973.

[2] SU Huai-zhi, HU Jiang, WEN Zhi-ping. Service Life Predicting of Dam Systems with Correlated Failure Modes [J]. Journal of Performance of Constructed Facilities, 2013, 27(3):252-269.

[3] Stone and Webster Engineering Corporation. Uplift Pressures, Shear Strengths, and Tensile Strengths for Stability Analysis of Concrete Gravity Dams [R]. California: EPRI, 1992.

[4] FISHMAN Y A. Features of Shear Failure of Brittle Materials and Concrete Structures on Rock Foundations [J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(6): 976-992.

[5] FISHMAN Y A. Stability of Concrete Retaining Structures and Their Interface with Rock Foundations [J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46(6): 957-966.

[6] 胡 江. 混凝土坝老化病害及其影响的递进分析方法[D]. 南京: 河海大学, 2013. (HU Jiang. Hierarchical Analysis Methods of Aging and Degradation Actions and Their Influences on Concrete Dams[D]. Nanjing: Hohai University, 2013. (in Chinese))

[7] 顾冲时, 苏怀智. 综论水工程病变机理与安全保障分析理论和技术[J]. 水利学报, 2007, (增1):71-77. (GU Chong-shi, SU Huai-zhi. Review on Theories and Technologies in Analyzing Serious Troubles Mechanism and Ensuring Safety of Hydraulic Engineering[J]. Journal of Hydraulic Engineering, 2007, (Sup.1):71-77. (in Chinese))

[8] 祁顺彬, 王向东. 考虑开裂约束的重力坝体型优化设计[J]. 长江科学院院报, 2008, 25(6):106-109. (QI Shun-bin，WANG Xiang-dong. Shape Optimization Design of Gravity Dam Considering Crack Constraint[J]. Journal of Yangtze River Scientific Research Institute, 2008, 25(6):106-109. (in Chinese))

[9] 殷德胜, 汪卫明. 大坝/地基系统应力-应变分析的不连续有限元法[J]. 岩石力学与工程学报, 2010, 29(12):2449-2455. (YIN De-sheng，WANG Wei-ming. Discontinuous Finite Element Method for Stress-strain Analysis of Dam/foundation System[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(12):2449-2455. (in Chinese))

[10] 吴世伟, 李同春. 重力坝最大可能破坏模式的探讨[J]. 水利学报, 1990, (8): 20-28. (WU Shi-wei, LI Tong-chun. An Approach to the Most Possible Failure Mode of Gravity Dams[J]. Journal of Hydraulic Engineering, 1990, (8): 20-28. (in Chinese))

[11] 郝明辉, 张艳红, 陈厚群. 基于材料非线性的坝体-地基体系损伤本构模型研究[J]. 水力发电学报, 2011, 30(6):30-33. (HAO Ming-hui, ZHANG Yan-hong, CHEN Hou-qun. Constitutive Model of Dam-foundation System Damage for Nonlinear Materials[J]. Journal of Hydroelectric Engineering, 2011, 30(6):30-33. (in Chinese))

[12] ICOLD. Dam Failures: Statistical Analysis ICOLD Bulletin 99 [M]. Paris: International Commission on Large Dams, 1995.