基于博弈论组合赋权的边坡稳定性集对分析
2014-08-17,,,
,,,
(南华大学 城市建设学院,湖南 衡阳 421000)
1 研究背景
边坡稳定性问题一直是岩土工程领域的一个重要研究课题,能否正确评价其稳定性直接关系到人民的生命财产安全。在我国已受到边坡灾害威胁和可能受到边坡灾害威胁的地区约占全国陆地面积的1/5~1/4,每年因边坡灾害造成的损失达60亿元以上,给国家和人民生命财产带来巨大损失,其危害十分巨大[1]。由于边坡稳定受多种因素的综合影响,各影响因素不但具有随机性、模糊性等不确定性的特点,还与边坡稳定性之间呈复杂的非线性关系,这就导致了确定性及线性分析方法难以对边坡的稳定性做出准确评价[2]。传统广泛使用的分析方法有极限平衡法和数值分析法[3-8]。然而这些方法都是依据相应的力学理论的前提下评价边坡的稳定性,其精度对岩土本构模型的选择和输入参数准确性均有较高的要求,由于岩土边坡稳定性的影响因素复杂多变,参数不准和模型不准已成为极限平衡法与数值模拟的2大瓶颈[9]。近年来,随着人们对边坡稳定性问题研究的不断加深,一些学者开始将模糊数学理论引入进来,从定性和定量2个方面来研究边坡的稳定性,以更好地体现岩土边坡非确定性的特征。薛新华等[10-11]根据边坡稳定性影响因素的特点,利用神经网络可以对信息并行处理和非线性映射的特点,建立了基于神经网络的边坡稳定性评价模型,分别利用遗传算法的模糊神经网和自组织特征映射神经网对收集到的边坡样本进行评价,为边坡稳定性评价提供了一种新的方法;李元松等[12]将模糊逻辑推理融入到神经网络非线性计算中,视整个边坡的稳定状态为同一变形规律的评价模式,对施工期间岩土边坡进行了综合评价;G.R.Dodagoudar和G.Venkatachalam[13]将模糊集理论引入到岩土边坡稳定性分析中来,将不确定性参数作为模糊集,用模糊不确定性的方法对其进行逻辑和系统分析,并给出了具体的分析过程;黄建文等[14]建立了岩土边坡稳定性模糊综合评价模型,运用层次分析法确定评价指标的权重,采用模糊数学方法对边坡的稳定性进行综合评价;付士根[15]将模糊分析理论和随机可靠性分析相结合,提出了边坡模糊随机可靠性分析的点估计法,应用统计矩点估计方法估计边坡的安全系数均值和可靠度,得出边坡的失稳概率;朱玉平等[16]在综合探讨岩体质量、结构面特征、边坡几何条件等影响因素的基础上,将边坡系统看作部分信息已知、部分信息未知的灰色系统,建立了灰关联评价模型,为工程地质类比从常规定性分析向定量分析过渡提供了一种直观有效的处理方法;谈小龙等[17]应用物元理论和可拓集合关联函数,建立了多层次多目标的岩土边坡整体安全综合评价体系,并给出了安全评价等级标准,将其应用到了锦屏一级水电站左肩槽岩石高边坡的整体安全评价中,效果显著,具有一定的借鉴意义。综合以上研究可以发现,各种方法在实际工作中都有一定程度的应用,并取得一定评价效果,但由于其理论出发点不同,评价结果的准确率也有所差别,目前还没有标准的评价方法。
由于影响岩土边坡稳定性的因素复杂,评价指标与稳定等级之间存在着复杂的非线性关系,对于正确地评价边坡的稳定性增加了很大的不确定性。本文在借鉴前人研究的基础上,尝试运用集对分析理论来研究岩土边坡的稳定性。集对分析法是我国学者赵克勤于1989年首次提出的用于描述和处理综合集成问题的一种系统分析方法,目前已经在多个领域得到成功应用。本文综合集对分析法和博弈论,从新的角度探索岩土边坡稳定性评价方法。
2 基于博弈论的集对分析模型
2.1 集对分析基本原理
集对分析是用于处理不确定性问题的系统分析方法,其核心思想是将确定性与不确定性问题视为一个确定与不确定系统,将确定性分为“同一”与“对立”2个方面,将不确定性称为“差异”,用同一度、对立度、差异度来体现系统中各元素既相互联系、相互影响、相互制约,又在一定条件下相互转化的复杂关系[18]。通过引入联系度统一表示系统的各种不确定性。
假设有联系的2个集合A和B构成一个集对H(A,B),A和B共有N个元素,则其联系度可以表示为[19]
(1)
式中:S,F,P分别表示集对中2个集合元素相比较得到的同一性、差异性、对立性元素的个数;S/N,F/N,P/N分别表示2个集合的同一度、差异度、对立度,可分别记为a,b,c,且a+b+c=1;i,j分别表示差一度系数、对立度系数,有时可仅起标记作用。
式(1)即为常用的三元联系度表示式,可对bi项进行扩展,得到多元联系度的表示式,即
(2)
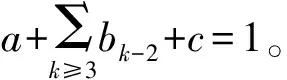
2.2 岩土边坡稳定性集对分析方法
岩土边坡稳定性评价实质是根据评价指标的实际值和各等级标准之间的相似性,对岩土边坡进行分类。首先,应当建立岩土边坡稳定性评价指标体系和评价等级标准。将待评价边坡的评价指标的实际值xl(l=1,2,…,n)记为集合Al,将相应的评价标准记为集合Bk(k=1,2,3,…,m),构成集对H(Al,Bk)。然后,构造联系度表达式。由于本文是将岩土边坡的稳定等级分为Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ 5个等级,即分别为稳定、较稳定、基本稳定、不稳定、极不稳定,所以需要构造5元联系度表达式。假设s1,s2,s3,s4分别为岩土边坡稳定性等级标准的门限值,见表1。

表1 评价标准示意
可以看出门限值的边界具有模糊性,规定若单个指标评价落入某个等级的情况视为同一,则指标落入相邻的范围视为差异,落入相隔的等级视为对立,即利用差异度分量解决等级边界模糊性的问题[20]。所以根据岩土边坡评价指标的特性,针对越小越优型的指标,其联系度计算表达式为
(3)
针对越大越优型指标,其联系度计算表达式为
(4)
通过式(3)和式(4)计算出各评价指标的联系度后,结合各评价指标的权重ωi,可计算出综合联系度为
(5)
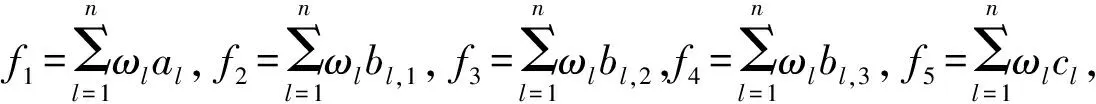
μA-B=f1+f2i1+f3i2+f4i3+f5j。
(6)
采用置信度准则来判定岩土边坡的稳定等级,即
hk=(f1+f2+L+fk)≥λ。
(7)
则可判断出待评岩土边坡的稳定性等级为k级。其中λ表示置信度,一般在[0.50,0.70]内取值,λ取值越大,则评价结果越保守、稳妥[20]。
2.3 基于博弈论的指标综合赋权
传统的确定评价指标权重的方法主要有层次分析法、熵权法、专家调查法、简单关联函数法等。通常采用某一种方法对评价指标赋权时,不是存在较大的主观因素的影响,就是没有考虑指标本身的问题重要性的差异。实际上,指标因素的重要性程度是客观存在的,并受到决策者主观意愿的影响,只有将主客观权重综合考虑在一起才能完全反映评价指标的重要性程度[21]。鉴于此,本文采用基于博弈论的综合赋权法,将由层次分析法确定的主观权重与由熵权法[18]确定的客观权重相结合,从而得到岩土边坡稳定性评价指标的综合权重。具体算法如下[22]:
对于多指标评价系统,假设采用L种方法得到指标的权重,记权重向量为
ωk=(ωk1,ωk2,…,ωkn), (k=1,2,…,L);
(8)
由此可以得到一个基本的权重集ω,L种权重向量的线性组合为
(9)
为了选择出最满意的权重向量ω*,需对线性组合系数ak进行优化,从而使ω与每个ωk的离差极小化,由此,可导出对策模型:
(10)
则根据矩阵的微分性质,可导出式(10)的最优化一阶导数条件为
(11)
由式(11)可以求得(a1,a2,…,aL),然后由(12)式对其进行归一化处理,即可得到综合权重向量ω*。
(12)
(13)
3 实例分析
3.1 确定评价指标和评价标准
岩土边坡的变形失稳是在众多因素的共同影响下发生的,由于各种因素的作用机理不同,使得岩土边坡的破坏具有复杂性和不确定性。根据统计资料和近年来的研究发现,岩土边坡的破坏除了与边坡地质体自身因素有关外,在一定程度上还受到外界因素的干扰。所以,准确地选取评价指标和评价标准也就显得至关重要。本文在综合前人研究的基础上,为验证基于博弈论组合赋权的岩土边坡稳定性集对分析模型的合理性和可行性,特选取文献[23]中的案例为评价对象,评价标准如表2所示。
坡1是渝黔高速公路某边坡,位于丘陵斜坡地带,坡高为46 m,边坡坡角约为64°,边坡岩体结构为上部砂岩,下部为泥沙层;坡2至坡4为首钢某矿区边坡,位于华北地台北缘、燕山沉降带中部。各边坡的具体数据见表3,其具体地质状况介绍见文献[23],在此不再详细叙述。

表2 边坡稳定性评价标准

表3 待评边坡评价指标实测值
3.2 基于博弈论的综合赋权指标权重的确定
本文客观权重采用文献[18]中熵权法确定,根据表3中待评边坡评价指标的实测值可以得到归一化后的判断矩阵为:

由熵权法理论可以求得评价指标的客观权重为ω1=(0.143,0.141,0.143,0.142,0.141,0.143,0.147)。
主观权重采用层次分析法[23],并经过一致性检验后所确定的权重为ω2=(0.034,0.378,0.023,0.150,0.094,0.057,0.250)。
可以看出,主客观权重还是存在一定的差异的,有必要进行权重的集成。根据式(11)可以得到博弈论综合赋权的最优化一阶线性方程组为
3.3 计算联系度及等级评定
由表2可知,既有成本型评价指标,又有效益型评价指标,所以针对不同类型的评价指标分别利用式(3)、式(4)计算其联系度,如表4所示。根据置信度识别原则,本文取置信度λ=0.6,可以识别出各岩土边坡的稳定等级,验证本文所建模型的适用性,并与灰关联分析和可拓评价的结果进行对比,如表4所示。

表4 边坡稳定性评价结果对比
从表4可以看出,坡1的稳定性最差,属于极不稳定级别,今后不仅要加大对其监测力度,还要采取有效的加固措施以降低发生滑坡的可能性,其余边坡的稳定状态都较好,但采取一定的监测手段和正常的日常维护是必不可少的。通过对比可以发现,本文所建模型的评价结果与其他方法比较一致,只有坡3的评价结果不同。实际上,单对坡3从定性分析的角度出发就不难发现,7项评价指标中就有4项指标属于较稳定级别,只有1项属于稳定级别,即坡3属于较稳定的可能性比较大,更偏向于Ⅱ级,凸显出本文的评价结果更加合理。
4 结 论
(1) 岩土边坡稳定性评价是一种多目标评价问题,评价指标赋权是否合理将会严重影响评价结果的准确率。本文基于博弈论综合赋权的优化模型,将层次分析法确定的主观权重与熵权法确定的客观权重融合为一个统一的权重,既兼顾了人为主观意愿的影响,又可以体现指标实测值的贡献,增强了评价结果的合理性。
(2) 岩土边坡稳定性评价涉及众多不确定因素,且指标与稳定等级之间存在着复杂的非线性关系。本文尝试应用集对分析理论构建岩土边坡稳定性评价模型,既考虑了等级标准边界的模糊性,又可以避免差异不确定性系数取值难的问题,结合置信度准则确定边坡稳定等级,还可以避免“最大隶属度”准则和“取大取小”算法丢失部分评价信息的问题,评价结果比较稳定可靠。对比发现,评价结果与其他方法比较一致,进一步说明了该方法的有效性,为边坡的稳定性分析提供了一种新的方法。
参考文献:
[1] 谢全敏, 陈立文, 夏元友. 基于案例挖掘的边坡稳定性智能评价系统研究[J]. 岩土力学, 2008, 29(1): 145-148.(XIE Quan-min, CHEN Li-wen, XIA Yuan-you. Study on Intelligent Evaluation System of Slope Stability Based on Case Mining [J]. Rock and Soil Mechanics, 2008, 29(1): 145-148. (in Chinese))
[2] 郭瑞清, 木合塔尔·扎日, 刘新喜. 基于自适应神经元模糊推理系统的岩质边坡稳定性评价方法[J]. 岩石力学与工程学报, 2006, 25(增1): 2785-2789. (GUO Rui-qing, ZARI M, LIU Xin-xi. Stability Evaluation Method of Rock Mass Slope Based on Adaptive Neural-net Work Based Fuzzy Interference System [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Sup.1): 2785-2789. (in Chinese))
[3] 曾亚武, 田伟明. 边坡稳定性分析的有限元法与极限平衡法的结合[J]. 岩石力学与工程学报, 2005, 24(增2): 5355-5359. (ZENG Ya-wu, TIAN Wei-ming. Slope Stability Analysis by Combining FEM with Limit Equilibrium Method [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(Sup.2): 5355-5359. (in Chinese))
[4] 方 薇, 杨果林, 刘晓红, 等. 非均质边坡稳定性极限分析上限法[J]. 中国铁道科学, 2010, 31(6):14-20. (FANG Wei, YANG Guo-lin, LIU Xiao-hong,etal. The Upper-bound Limit Analysis of the Inhomogeneous Slope Stability [J]. China Railway Science, 2010, 31(6): 14-20.(in Chinese))
[5] 郭明伟, 李春光, 王水林. 基于有限元应力的三维边坡稳定性分析[J]. 岩石力学与工程学报, 2012, 31(12): 2494-2500. (GUO Ming-wei, LI Chun-guang, WANG Shui-lin. Three-dimensional Slope Stability Analysis Based on Finite Element Stress [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(12): 2494-2500. (in Chinese))
[6] 陈国庆, 黄润秋, 周 辉, 等. 边坡渐进破坏的动态强度折减法研究[J]. 岩土力学,2013,34(4):1140-1146. (CHEN Guo-qing, HUANG Run-qiu, ZHOU Hui,etal. Research on Progressive Failure for Slope Using Dynamic Strength Reduction Method [J]. Rock and Soil Mechanics, 2013, 34(4): 1140-1146. (in Chinese))
[7] 肖锐铧, 王思敬, 贺小黑, 等. 非均质边坡多级稳定性分析方法[J]. 岩土工程学报,2013,35(6):1062-1068.(XIAO Rui-hua, WANG Si-jing, HE Xiao-hei,etal. Multi-level Stability Analysis of Inhomogeneous Slopes [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1062-1068. (in Chinese))
[8] 郭院成, 陈 涛, 钱 辉. 基于强度折减的边坡动力安全系数确定方法研究[J]. 土木工程学报, 2012, 45(增2): 117-120. (GUO Yuan-cheng, CHEN Tao, QIAN Hui. The Determination Method of Dynamic Safety Factor for Slope Based on Strength Reduction [J]. China Civil Engineering Journal, 2012, 45(Sup.2): 117-120. (in Chinese))
[9] 刘勇健, 李彰明, 杨雪强. 岩质边坡稳定性评价的粗糙集-支持向量机方法[J]. 工程地质学报, 2009, 17(3): 322-328. (LIU Yong-jian, LI Zhang-ming, YANG Xue-qiang. Rough Set and Support Vector Machine Based Method for Evaluation of Rock Slope Stability [J]. Journal of Engineering Geology,2009,17(3):322-328.(in Chinese))
[10] 薛新华, 张我华, 刘红军. 基于遗传算法和模糊神经网络的边坡稳定性评价[J]. 岩土力学, 2007, 28(12): 2643-2648. (XUE Xin-hua, ZHANG Wo-hua, LIU Hong-jun. Evaluation of Slope Stability Based on Genetic Algorithm and Fuzzy Neural Network [J]. Rock and Soil Mechanics, 2007, 28(12): 2643-2648. (in Chinese))
[11] 薛新华, 张我华, 刘红军. 基于SOFM 神经网络的边坡稳定性评价[J]. 岩土力学, 2008, 29(8): 2236-2240. (XUE Xin-hua, ZHANG Wo-hua, LIU Hong-jun. Evaluation of Slope Stability Based on SOFM Neural Network [J]. Rock and Soil Mechanics, 2008, 29(8): 2236-2240. (in Chinese))
[12] 李元松, 陈文峰, 李新平, 等. 基于模糊神经网络的边坡稳定性评价方法[J]. 武汉理工大学学报, 2013, 35(1): 113-118. (LI Yuan-song, CHEN Wen-feng, LI Xin-ping,etal. Stability Assessment of Rock Slope Based on Fuzzy Neural Network [J]. Journal of Wuhan University of Technology, 2013, 35(1): 113-118. (in Chinese))
[13] DODAGOUDAR G R, VENKATACHALAM G. Reliability Analysis of Slopes Using Fuzzy Sets Theory [J]. Computers and Geotechnics, 2000, 27(2): 101-115.
[14] 黄建文, 李建林, 周宜红. 基于AHP的模糊评判法在边坡稳定性评价中的应用[J]. 岩石力学与工程学报, 2007, 26(增1): 2627-2632. (HUANG Jian-wen, LI Jian-lin, ZHOU Yi-hong. Application of Fuzzy Analysis Based on AHP to Slope Stability Evaluation [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Sup.1): 2627-2632. (in Chinese))
[15] 付士根. 基于模糊随机可靠性的边坡稳定性评价[J]. 中国安全生产科学技术, 2012, 8(8): 98-101. (FU Shi-gen. Stability Assessment of Opencast Mines Slope Based on Fuzzy Stochastic Reliability [J]. Journal of Safety Science and Technology, 2012, 8(8): 98-101. (in Chinese))
[16] 朱玉平, 莫海鸿. 灰关联分析法在岩质边坡稳定性评价中的应用[J]. 岩石力学与工程学报, 2004, 23(6): 915-919. (ZHU Yu-ping, MO Hai-hong. Application of Gray Correlation Analysis to Rock Slope Stability Estimation[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(6): 915-919. (in Chinese))
[17] 谈小龙, 徐卫亚, 梁桂兰. 可拓方法在岩石边坡整体安全评价中的应用[J]. 岩石力学与工程学报, 2009, 28(12): 2503-2509. (TAN Xiao-long, XU Wei-ya, LIANG Gui-lan. Application of Extenics Method to Comprehensive Safety Evaluation of Rock Slope [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(12): 2503-2509. (in Chinese))
[18] 孟宪萌, 胡和平. 基于熵权的集对分析模型在水质综合评价中的应用[J]. 水利学报, 2009, 40(3): 257-262. (MENG Xian-meng, HU He-ping. Application of Set Pair Analysis Model Based on Entropy Weight to Comprehensive Evaluation of Water Quality [J]. Journal of Hydraulic Engineering, 2009, 40(3): 257-262. (in Chinese))
[19] 王文圣, 金菊良, 李跃清. 基于集对分析的自然灾害风险度综合评价研究[J]. 四川大学学报(工程科学版), 2009, 41(6): 6-12. (WANG Wen-sheng, JIN Ju-liang, LI Yue-qing. Risk Degree Assessment of Natural Disaster Based on Set Pair Analysis Method [J]. Journal of Sichuan University (Engineering Science), 2009, 41(6): 6-12. (in Chinese))
[20] 李文宾, 姚阿漫. 基于熵权的五元联系数在地下水水质评价中的应用[J]. 水资源与水工程学报, 2013, 24(2): 118-120. (LI Wen-bin, YAO A-man. Application of Five-element Connection Number in Evaluation of Groundwater Quality Based on Entropy [J]. Journal of Water Resources & Water Engineering, 2013, 24(2):118-120. (in Chinese))
[21] 尚俊龙, 胡建华, 莫荣世, 等. 可爆性分级的博弈论-物元可拓预测模型及其应用[J]. 采矿与安全工程学报, 2013, 30(1): 86-92. (SHANG Jun-long, HU Jian-hua, MO Rong-shi,etal. Predication Model of Game Theory-matter-element Extension for Blast Ability Classification and Its Application [J]. Journal of Mining & Safety Engineering, 2013, 30(1): 86-92. (in Chinese))
[22] 张志清, 陈 瑞,沈 忱, 等. 基于博弈论的可拓评价方法在城市轨道交通路基养护质量评价中的应用[J]. 武汉理工大学学报(交通科学与工程版), 2012, 36(4): 691-694. (ZHANG Zhi-qing, CHEN Rui, SHEN Chen,etal. Application of Extension Assessment Method Based on Game Theory to Evaluate the Maintenance Quality of Urban Rail Transit Subgrade [J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2012, 36(4): 691-694. (in Chinese))
[23] 丁丽宏. 基于改进的灰关联分析和层次分析法的边坡稳定性研究[J]. 岩土力学, 2011, 32(11): 3437-3441. (DING Li-hong. Research on Estimation of Slope Stability Based on Improved Grey Correlation Analysis and Analytic Hierarchy Process [J]. Rock and Soil Mechanics, 2011, 32(11): 3437-3441. (in Chinese))
