卡门常数研究现状及存在的问题

，，，

(长江科学院 河流研究所, 武汉 430010)

1 研究背景

自从1895年雷诺(O’Reynolds)由时均概念出发研究N-S方程从而导出了雷诺方程以后，雷诺方程便成了现代紊流研究的基础，但是在后来的研究中一直未能从根本上解决雷诺方程的封闭问题，这给紊流理论研究和工程技术实际应用都带来了一定困难。于是，1925年普朗特提出了混合长度假说和动量理论[1]，他的理论精髓为

(1)

式中：τ为紊动应力；ρ为密度；u′,ν′均为脉动流速；l为普朗特长度；y为深度；u为深度y处的流速。

紊流研究进展到这一阶段之后，进一步的工作是决定紊流的混掺长度从而推导流速分布。根据混掺长度理论不难推断混合长度与流速没有关系，而只是水流中所处位置的函数。于是，1934年T.Von Karman[2]提出了紊流局部运动相似理论，在该理论中引入了一量纲常数k作为比例系数，并且给出了混合长度计算公式，即

(2)

式中k为卡门常数。

根据尼古拉兹试验，清水管流中卡门常数k为0.4，冠利根[3](G.H.Keulegan)分析了巴津(H.E.Bazin)的试验资料，证明在不同形状及糙率的明渠清水流中，卡门常数k亦为0.4，只有在挟沙水流中，卡门常数k因挟沙浓度或理查逊数Ri(挟沙浓度梯度)及垂线位置而异。在1933年，Taylor提出了涡旋传递理论，指出在液团脉动过程中动量必然要发生变化，紊动过程中紊动切力形成涡量，故涡量保持守恒，而不是动量保持不变[4]。但是涡量传递理论与动量传递理论都归结于混掺长度，所以没有多大的价值。由上述可知，卡门常数k是关于混掺长度和速度廓线的经验系数，在清水中其值是0.4，在浑水中它是一变量。

2 卡门常数k的实质及用途

2.1 卡门常数k的实质

固液两相流是一种复杂的运动，泥沙在水流的影响下运动反过来又影响水流的运动，卡门常数k是水动力学、泥沙运动学和流体力学中的一个重要参数，鉴于此，有必要探究卡门常数k的实质。根据实测资料，在黏性层以上直至y/h=0.1～0.2这一范围内，流速梯度很好地满足下式：

(3)

式中：h为水深；u*为深度y处的摩阻流速。

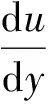
2.2 卡门常数k的用途

2.2.1 预测流速分布

目前，固液两相流流速分布有2种模式，其一就是变k模式，持这种观点的人占大多数，而变k模式中最有影响的流速分布公式就是卡尔曼-勃兰德对数公式[6]，即

(4)

式中umax为深度y处的最大流速。

根据式(4)可以计算出流速廓线。

2.2.2 计算泥沙悬浮指标

20世纪30年代劳斯(H.Rouse)指出悬浮指标的计算公式为

z=w/(ku*)。

(5)

式中：w为悬浮泥沙的沉速；z为悬浮指标，是量纲为一的数，反映了重力作用与紊动扩散作用的相互对比关系[7]。其中，重力作用通过w来表达，紊动作用通过ku*来表达。z越大，则表示重力作用相对较强，紊动作用难以把泥沙扩散到水体表面，悬移质将集中在离床面不远处，于是在相对平衡情况下，含沙量垂线分布就不均匀；反之，z越小，紊动作用相对越强，在相对平衡状态下，含沙量垂线分布就越均匀。但是在实际工程应用中，发现泥沙颗粒较细、含沙量较小时，计算值与实际值比较一致；泥沙颗粒较粗、含沙浓度较大时，计算值与实际值就有很大的偏差。限于篇幅，关于z，w和k的关系不再赘述。

2.2.3 计算混掺长度

Prandtl将紊流运动与分子扩散相类比，认为紊流是由许多液体质点相结合成的液体团运动。液体团在一定距离内本身保持不变，它所具有的量从一个地方到另一个地方不发生量的输运，液体团到达新的位置后才与当地流体团具有的量相混合[4]。因此得到的紊动剪力表达式为

(6)

对于二维流，剪切力可以表达为

(7)

式中γ为重度。

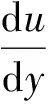
(8)

通过仔细分析，这种演算只是在数学上成立，而从物理图形上来讲，则存在明显的矛盾，由于混掺理论本身并不能够提供一个l的理论表达式，所以l的选取还停留在猜测的阶段，但是在实用中掺长优于任何被用来改进的新的掺长。

3 卡门常数k的研究现状

3.1 卡门常数k的影响因素

固液两相流的能量分配机制至今仍不十分清楚，观点各异:R.T.Knapp[8]考虑了水流和悬浮颗粒的能量交换，并认为向下游运动的颗粒在竖直方向下降所提供的能量应该与为保持颗粒悬浮所消耗的能量相等;R.A.Bagnold[9]认为水流用以支配颗粒悬浮的能量应是水流提供的能量与颗粒自身提供给水流的能量之差，能量分配机制中较有影响的是Velikanov的“重力理论”。该理论认为，固液混合体消耗的总能量应为清水阻力所消耗的能量与水流悬浮颗粒的能量之和[4]。

对卡门常数的研究能够有助于了解固液两相能量分配机制和验证机制是否正确，而且为了解水流的结构，本文主要是从影响流速的分布角度，讨论卡门常数的影响因素。

3.1.1 泥沙特性

泥沙特性包括含沙量、泥沙粒径、级配、黏度、沉速和相对密度。室内试验资料和野外观测资料表明，挟沙水流的流速梯度大于清水的流速梯度，在近底区含沙量大，颗粒又较粗，使底部流速减小，流速分布变得不均匀，k值变小。

3.1.2 泥沙运动状态

根据泥沙在水流中的运动状态，泥沙运动包含推移质、悬移质运动，泥沙中推移质有跃移、平动等形式，泥沙在运动过程中增加了水流能量损失；水流紊动为悬移质提供能量，因此使局部能量增加，传递能减少。相应地造成当地水流流速减少，流速分布更不均匀。流速分布愈不均匀，卡门常数愈小。

3.1.3 河床形态

河床中有深槽、浅滩、沙波等，这使水流具有较强的三维特征，三维特征的存在明显影响了流速分布的均匀程度，这时卡门常数k取决于床面形态。

3.2 卡门常数k的确定方法

3.2.1 从能量角度来研究k值的变化规律

H.A.Einstein和钱宁[10]首先从能量的角度来分析悬移质的存在对卡门常数的影响，并绘制了参数E和卡门常数的关系图，如图1[10]所示。参数E的表达式为

(9)

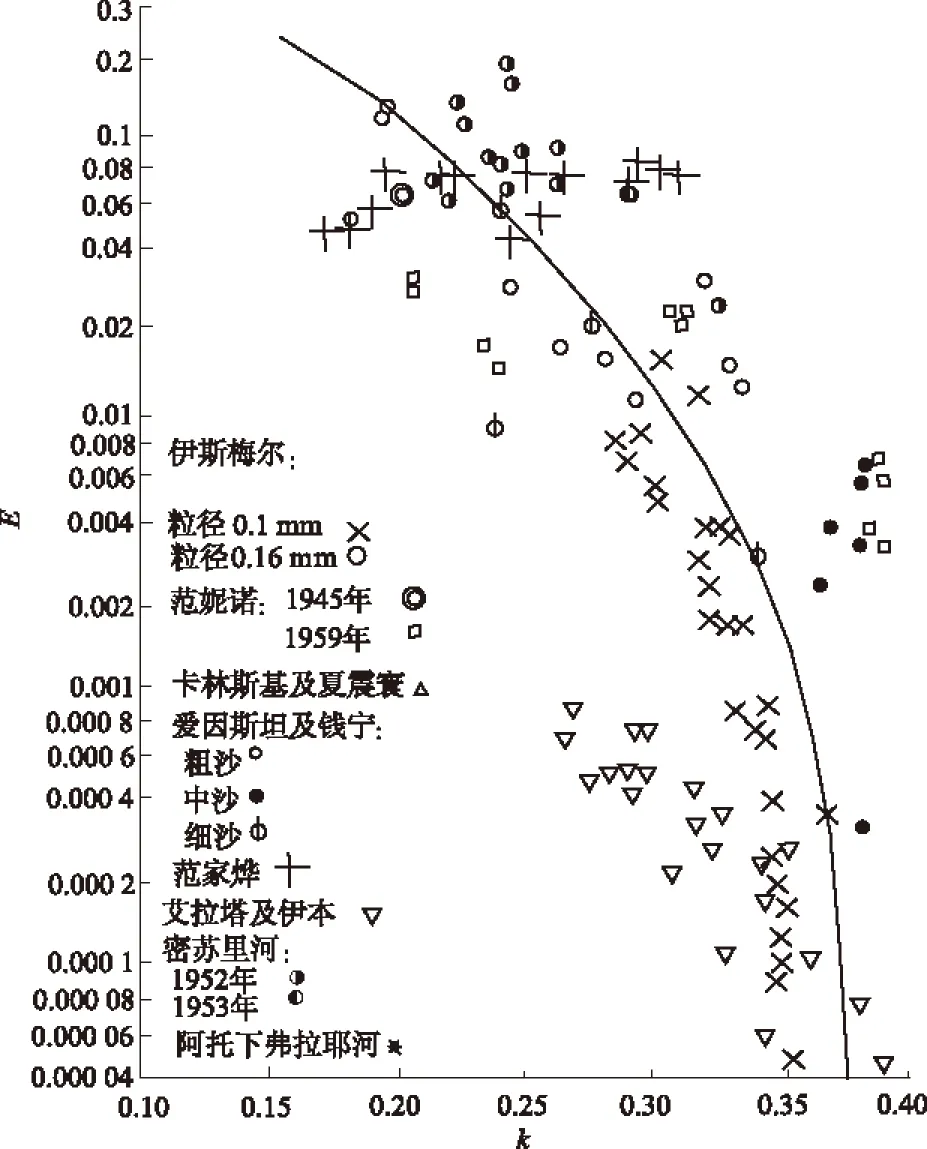
图1 E和k关系图

3.2.2 从密度梯度角度探求k的变化规律

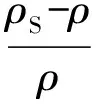
图2 k和关系图

3.2.3 根据流速廓线来研究k的变化规律

对于固液两相流的流速分布，学者们还未形成统一的认识。1988年，倪晋仁和惠遇甲[12]根据收集到的水槽资料发现，流速试验资料的变化趋势颇为一致，即将流速分布归纳为2种类型，即Ⅰ型和Ⅱ型。认为采用分段法可以将流速分布统一，于是将流速分布沿垂线分段，使得变k模式和Coleman模式得到统一。分段法描述流速如下：

(10)

式中：um为浑水的流速；k0=0.4。其中，根据分段流速值在η处令流速上下2式相等得到交点η的表达式为

(11)

3.2.4 量纲分析k的变化规律

根据影响因素，建立挟沙水流卡门常数与主要因素的关系式[13]为

k=f(S,μ,ρ,ρS,P,d,ω,u*)。

(12)

式中：S为含沙量;ρ,ρS,P,d,ω,u*均为动力黏滞系数。P为悬移质级配，表示不同粒径组的泥沙在悬移质中所占的百分比，d为泥沙粒径。

以d，ω和ρ为基本变量，按照量纲分析原理式(12)变为

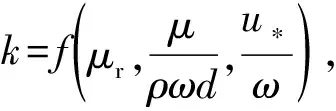
(13)

式中：A=B+1.5B2；B=ur-0.999；k0=0.4；m=0.18-0.03lg(h/d)。

由式(13)可以看出，在低含沙水流条件下，泥沙粒径对卡门常数的影响起主导作用；在高含沙水流条件下，泥沙浓度或动力黏滞系数对卡门常数起主导作用。

3.2.5 从力学角度来研究k的变化规律

钱宁和万兆惠[1]认为由于颗粒碰撞切应力的存在使得近底层的流速分布规律与主流区不同。R.A.Bagnold[14]对近底层的泥沙运动规律的研究认为，在近底层除了紊动剪切力外，泥沙的运动还存在颗粒碰撞切应力。因此，挟沙水流剪切力τ由2部分组成，即

τ=τf+τs。

(14)

式中：τf为紊动附加切应力；τs为颗粒剪切力。

在二维明渠均匀流中，距河床y处的挟沙水流的紊动剪切力τ可表示为

(15)

根据R.A.Bagnold[14]的研究，距河床y处的颗粒剪切力τs的表达式为[15]

(16)

式中：a为常数，a=0.013；λ为与泥沙浓度有关的常数，可以表示为

(17)

式中：C为y处的泥沙体积浓度；C0为静止状态下天然泥沙的最大体积浓度，取C0=0.6，可得

(18)

其中，

(19)

(20)

式中b=0.01h，选择b在近地层，在近底层泥沙的卡门常数是定值，即为0.4。式(20)表明，主流区的卡门常数与底层泥沙浓度有关。

3.2.6 从黏度分析k的变化规律

对于挟沙水流，黏度是描述含沙浓度和泥沙级配的最佳参数，舒安平等[16]通过数值拟合得

(21)

相对黏度采用费祥俊公式，k值表达式为

(22)

式中：Sv为体积比含沙浓度；Svm为泥沙极限浓度。

3.2.7 从浓度分析k的变化规律

张红武[17]利用大量室内和天然河流的试验资料，点绘了k和Sv的关系曲线，如图3所示。在图中，尽管k和Sv的关系点较为分散，但是变化趋势还是显而易见的。

图3 含沙量Sv和k关系图

由图3可得关系式

(23)

3.2.8 从自动悬浮角度分析k的变化规律

王尚毅[18]运用Bagnold的“自动悬浮”论点，认为由于悬浮颗粒的存在而消耗的能量可以从悬浮颗粒本身提供水流的势能中获得补偿，并因此得到临界表达式：

ω=uJ。

(24)

式中：ω为分界粒径对应的颗粒沉降速度;u为断面平均流速。当ω=uJ时，卡门常数与含沙量浓度无关；而当ω

(25)

4 卡门常数研究问题和展望

作为描述水流结构的重要参数，其影响因素众多，研究人员只是取了其中的部分因素来研究，无法全面地描述挟沙水流中卡门常数的定量变化。

从能量角度探求k值的变化规律中，固液两相流的能量分配机制本来就不是很清楚，现在假设其能量分配机制正确，参数E作为描述卡门常数的唯一参数，结合其物理意义，参数E中Σ是对悬移质组成中不同的ω部分进行总和，这样就带来了一些问题：当泥沙颗粒较粗时，泥沙主要集中在床面附近运动，在此处形成了一个很大的密度梯度；而在床面以外极大部分的主流区，含沙量的梯度就比较小，这种情况下，支持悬移质所消耗的能量集中在河床附近一个较小的流区内，这样所消耗的能量按水深进行平均，相当于把能量集中消耗的程度冲淡了，而且这一影响在不同的水流及泥沙条件下是不同的，这样E作为一个参数的意义就大为削弱了。

从密度梯度探求的卡门常数k值变化规律中，沿着水深垂向悬移质浓度是变化的，而这一变化采用理查逊数来表示，采用一个高程上的理查逊数作为特征值，并且考虑床面平整和床面存在沙波的情况，H.A.Einstein和张红武等都绘制了参数和卡门常数k的关系图，但未给出其与卡门常数k的定量关系式，在实际应用中不是很方便。

上述2种研究方法都是研究卡门常数的早期代表。由速度轮廓线推出的卡门常数公式认为，在挟沙水流中流速分布不是对数分布，而是在水流流速分布中有一尾流函数。倪晋仁和惠遇甲[12]通过对清水和浑水的比较得出了尾流的函数表达式，经过一系列的等价变换得出了卡门常数的表达式。看起来是很严密的理论推导，但是公式的建立是在流速分布的结构上来推导的，而事实上对变k模式和Coleman模式统一的流速公式是假设的，同时还有k测和k算的验证中取了水面浓度为0这一缺陷。

从量纲来分析卡门常数k的变化规律中，周宜林等[13]将泥沙影响的主要因素都考虑进去；与其形成鲜明对比的是舒安平等[16]从黏度和张红武[17]从浓度来分析卡门常数的变化规律，他们推导的公式都是拟合的结果，从验证的结果来看量纲分析的结果拟合效果较佳，可以说他们的思想都是相近的，因为黏度也是浓度不同的反映。张红武从浓度角度分析的公式是一个隐形公式，卡门常数k值的求解需要通过浓度这个参数来求，而浓度计算本身是需要k值作为参数的，这样就不方便于实际应用，并且舒安平等[16-17]模拟和验证公式所收集的试验资料纷繁芜杂，没有经过系统的试验。

从力学角度推导的结果考虑了紊动剪切力和碰撞剪切力，这种方法值得推崇，但是这种考虑值得商榷和检验，而且考虑底部参考点浓度时不够严谨，这就为今后研究卡门常数提出了更高的要求：要有更好的试验条件和更精准的数据处理。

5 结 语

卡门常数作为描述水流结构的重要参数，在清水中其值平均值为0.4，基本不变；在挟沙水流中，卡门常数为一变量。固液两相流中，固体和液相相互作用，固体在水流作用下发生运动，而固体颗粒的存在又反过来影响水流的紊动结构，为了深入了解水流结构，本文总结了前人对卡门常数的研究结果，为以后继续了解卡门常数提供一点帮助。

参考文献：

[1] 钱 宁，万兆惠. 泥沙运动力学[M]. 北京：科学出版社，1991：95.(QIAN Ning，WAN Zhao-hui. Sediment Transport Mechanics[M]. Beijing：Science Press，1991:95.(in Chinese))

[2]VON KARMAN T.Turbulence and Skin Friction[J].Journal of the Aeronautical Science，1934，1(1)：1-20.

[3] KEULEGAN G H. Laws of Turbulent Flow in Open Channels[J].Journal of Research of the National Bureau of Standards，1938,21：701-741.

[4] 倪晋仁，王光谦，张红武. 固液两相流基本理论及其最新应用[M]. 北京：科学出版社，1991：87. (NI Jin-ren，WANG Guang-qian，ZHANG Hong-wu. Basic Theories of Solid-liquid Two-Phase Flow and Their Recent Applications[M]. Beijing：Science Press,1991:87.(in Chinese))

[5] 秦荣昱. 动床水流卡门常数变化规律的研究[J].泥沙研究，1991，(3)：38-52.(QIN Rong-yu. Karman Coefficient of Flow with Movable Bed[J]. Journal of Sediment Research,1991，(3)：38-52.(in Chinese))

[6] 舒安平. 高含沙水流挟沙能力及输沙机理的研究[D]. 北京：清华大学，1994.(SHU An-ping. Study on the Transport Capacity or Hyper-concentrated Silt-laden flow and the Mechanism of Sediment Transport[D]. Beijing：Tsinghua University，1994.(in Chinese))

[7] 李光炽. 河流动力学[M]. 南京：河海大学出版社，1990:63.(LI Guang-chi. River Dynamics[M]. Nanjing: Hohai University Press, 1990: 63. (in Chinese))

[8]KNAPP R T.Energy-balance in Stream-flows Carrying Suspended Load[J].Transactions of American Geophysical Union, 1938, 19(1): 501-505.

[9]BAGNOLD R A.Auto-suspension of Transported Sediment, Turbidity Currents[J].Proceedings of the Royal Society of London. Series A，Mathematical and Physical Sciences, 1962, 265(1322): 315-319.

[10] CHIEN N,EINSTEIN H A.Effects of Heavy Sediment Concentration near the Bed on Velocity and Sediment Distribution[M]. Missouri：Missouri River Division, Corps of Engineers, US Army, 1955.

[11] BARTON J R, LIN P N. Roughness of Alluvial Channels[R]. Colorado：Civil Engineering Department，Colorado Agriculture and Mechanic College, 1955.

[12] 倪晋仁，惠遇甲. 浑水流速分布与悬移质浓度 分布的关系[J]. 泥沙研究，1988，(2):17-28. (NI Jin-ren，HUI Yu-jia. Relation Between the Velocity Distribution and the Suspended Concentration Distribution[J]. Journal of Sediment Research，1988，(2):17-28.(in Chinese))

[13] 周宜林, 唐洪武,闫 静，等. 挟沙水流卡门常数的影响因素[J]. 泥沙研究，2008，(3)：51-56.(ZHOU Yi-lin，TANG Hong-wu，YAN Jing,etal. Influence Factors of the Von Karman Constant for Sediment-Laden Flows[J]. Journal of Sediment Research，2008，(3):51-56.(in Chinese))

[14] BAGNOLD R A. Experiment on a Gravity-free Dispersion of Water Flow[J]. Proceedings of the Royal Society of London. Series A，Mathematical and Physical Sciences,1954, 225(1160): 49- 63.

[15] 黄才安，龚敏飞，陈志昌，等. 挟沙水流卡门常数的理论研究[J]. 长江科学院院报，2005，22(5):8-10.(HUANG Cai-an，GONG Min-fei，CHEN Zhi-chang,etal. Theoretical Study on Kaman Constant in Sediment-Laden Flow[J]. Journal of Yangtze River Scientific Research Institute，2005，22(5)：8-10.(in Chinese))

[16] 舒安平, 刘青泉,费祥俊. 高低含沙水流流速分布的统一规律[J]. 水利学报，2006，37(10)：1175-1180. (SHU An-ping，LIU Qing-quan，FEI Xiang-jun. Unified Laws of Velocity Distribution for Sediment Laden Flow with High and Low Concentration[J]. Journal of Hydraulic Engineering，2006，37(10)：1175-1180. (in Chinese))

[17] 张红武. 挟沙水流流速的垂线分布公式[J]. 泥沙研究，1995，(2)：1-10. (ZHANG Hong-wu. Vertical Distribution of Velocity in Sediment-laden Flow[J]. Journal of Sediment Research，1995，(2)：1-10.(in Chinese))

[18] WANG S Y. Variation of Karman Constant in Sediment-laden Flow[J]. Journal of Hydraulic Division，ASCE，1981,107(11):407-417.