基于四谱线插值FFT的电网谐波检测方法

郝柱，顾伟，褚建新，麻朝



基于四谱线插值FFT的电网谐波检测方法

郝柱，顾伟，褚建新，麻朝

（上海海事大学航运技术与控制工程交通部重点实验室，上海 201306）

在采用快速傅里叶变换法分析电网中各次谐波时，因信号的非整周期截断和非同步采样而造成的频谱泄露会对检测结果的准确性造成影响。为了提高谐波检测的准确度，提出了一种基于四谱线插值的快速傅里叶变换算法。该算法通过对加窗信号的离散频点处幅值信息的分析，利用谐波频点附近的四根谱线进行加权运算，进一步提高了谐波幅值和相位检测的准确度。通过数据拟合，得到常用的窗函数所对应的谐波分析实用修正公式。由数值仿真分析可以看出，该算法具有更高的检测精确度。仿真及实测的结果充分验证了该算法的准确性和有效性。

四谱线插值；快速傅里叶变换；谐波检测；窗函数；数据拟合

0 引言

在电力系统中，由于大量电子元器件和非线性负载的使用，电网受到的谐波污染越来越严重。为了能够有效地减少谐波污染，对电网中的谐波成分进行准确检测已经成为减少谐波污染、防止谐波危害、维护电网的安全运行的前提和关键。

目前电网谐波研究的方法有多种，包括快速傅里叶变换算法，瞬时无功功率检测方法以及神经网络算法等等，然而在实际工程应用中仍然以快速傅里叶变换(FFT)为主要研究方法。在应用FFT算法的同时，会存在频谱泄露问题，频谱泄漏包括长范围泄漏和短范围泄漏两部分，它们可以通过对信号加窗和频域信号插值运算来减小。加窗算法有很多种，常用的窗函数种类包括三角窗、Hamming窗、Hanning窗、Blackman窗等等，选择窗函数时可根据具体分析情况采用合适的窗函数。插值算法中有单谱线插值算法，双谱线插值算法[，三次样条插值算法，三谱线插值算法等。本文采用四谱线插值算法，与双谱线插值以及三谱线插值算法相比，该算法可以有效地提高谐波幅值与相位的检测精度。

1 四谱线插值算法

1.1插值算法频点附近谱线分析

目前双谱线插值算法的使用比较广泛，该方法利用谐波频点处邻近两条谱线幅值大小求取谐波的实际幅值和相位大小。尽管该方法与单谱线算法相比，在谐波检测准确度上有了一定提高，但是，该方法并没有充分利用谐波频点附近谱线中蕴含的信息。三谱线插值法利用频点位置附近的三条谱线进行幅相运算，与双谱线插值法比较，进一步提高了谐波测量的准确度，但是该算法并没有考虑到频点左右对称谱线所蕴含的信息量。图1为正弦信号加窗后在不同采样频率时其频点附近各谱线幅值信息。图1各图中的虚线为波形在频域图中不同采样频率时实际频点的位置，该采样信号幅值为100，频率为50 Hz。

从图1可以看出，距离频点最近的左右两条谱线所蕴含的幅值信息量最大，其次是外侧的两条谱线。三谱线插值算法采用频点左右的两条谱线加上这两条谱线外围两条谱线中的其中一条来求取信号幅值的大小，而并未利用外围的两条谱线的对称性。由图1 (b)、图1(d)可以看出，这两条谱线的幅值信息含量是基本上相同的。文中采用四谱线插值算法，充分利用了频点左右四条谱线的对称性，利用这四条谱线幅值来求取实际幅值和相位的大小。

1.2算法原理

(2)

对式(3)进行离散化，得到离散傅里叶变换的表达式为

(4)

图1正弦信号频点附近谱线值

因信号的非整周期截断和非同步采样，由图1可看出，通常峰值频率的谱线很难落到离散谱线的整数频点上，设峰值频率左右四条谱线的频率分别为、、、，其中、为距离峰值频点处最近的两条谱线，、为距离峰值频点处次近的两条谱线，则有，其中各值之间的关系为，，。令四条谱线对应的幅值分别为、、、，令处的幅值为，，，，，。引入参数,令，则，显然的取值范围关于原点对称，求取的值即可求出幅相的信息。令,,则根据公式(4)并将带入，得到

(6)

假设

则有

(8)

由图1可知，距离峰值频率最近的两条谱线所含信号幅值信息量最大，故在计算时给与这两条谱线更大的加权值，四条谱线的加权值分别为1、2、2、1。则

(10)

(12)

2 常用窗函数修正公式

(1) 三角窗函数

(2) Hanning窗函数

(3) Hamming窗函数

(4) Blackman窗函数

3 数值仿真及结果分析

3.1不同插值算法比较

3.1.1 与双谱线插值算法比较

为验证该算法的有效性，本文采用信号仿真生成器生成仿真信号，通过数据采集卡对仿真信号进行数据采集，对添加Hanning窗、Hamming窗、Blackman窗三种窗函数进行仿真对比。根据电网中电量信号的谐波次数为奇数这一特点设置仿真参数，信号生成各次谐波的频率、幅值以及相位如表1所示。采样频率为5 120 Hz，采样点数为30 000。

表1 基波与各次谐波的取样频率、幅值、相位

3.1.2与三谱线插值算法比较

为了与三谱线算法比较，本文采用参考文献[20]中的仿真信号进行比较，文献[20]采用的仿真信号的频率、幅值以及相位如表2所示。其中基波频率为50.1 Hz，采样频率为5 120 Hz，采样点数为1 024。

表2仿真信号构成

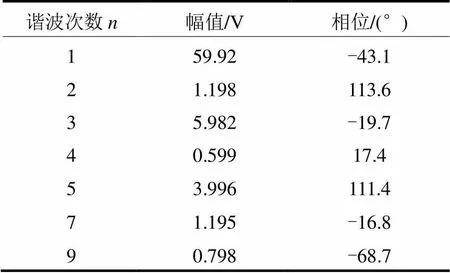
Table 2 Components of simulated signal

3.2结果分析

3.2.1 与双谱线插值算法比较分析

双谱线插值算法与四谱线插值算法在加汉宁窗、海明窗与布莱克曼窗三种窗函数的情况下，检测出来的幅值与相位的测量值如表3、表4所示。幅值与相位的测量误差结果如表5、表6所示。本文图表中采用的算数符号表示为，其中与为常数。

表3不同加窗插值算法对应的幅值测量结果

Table 3 Amplitude of measured results corresponded to different window interpolation algorithms V

表4不同加窗插值算法对应的相位测量结果

Table 4 Phase of measured results corresponded to different window interpolation algorithms (°)

表5不同加窗插值算法对应的幅值误差

Table 5 Amplitude errors of different window interpolation algorithms V

表6不同加窗插值算法对应的相位误差

Table 6 Phase errors of different window interpolation algorithms (°)

通过表5可以看出，在不同的窗函数条件下，四谱线差值算法的检测精度要比双谱线插值算法的检测精度高。从表6可以看出，在加海明窗与布莱克曼窗函数条件下，对相位的检测精度也有了一定的提高。在相位修正公式中与的拟合程度越高，相位检测的结果精度越高，而双谱线插值中汉宁窗因与的一阶线性关系，其相位检测精度虽然最高，但是其幅值检测的精度相对其他窗函数来说是最低的。在对幅值检测要求高的电网谐波检测中，通过表5、表6可以看出四谱线插值算法具有更高的检测准确性。

3.2.2与三谱线插值算法比较分析

文中选用与文献[20]中相同的采样频率以及采样数，测量结果中幅值与相位误差如表7、表8所示。

表7不同窗函数的幅值绝对误差

Table 7 Comparison of absolute error of amplitude in different window functions %

表8不同窗函数对应的相位绝对误差

Table 8 Comparison of absolute error of amplitude in different window functions (°)

通过表7、表8可以看出，在选择与文献[20]相同仿真条件的情况下，四谱线插值算法在幅值检测与相位检测上误差更小，检测精度更高。由此可知，四谱线差值算法在幅值检测与相位检测方面都要优于三谱线插值算法。

4 结论

使用快速傅里叶变换算法在求解各次谐波幅值与相位时，因频谱泄露产生的误差可以采用加窗函数和插值算法来减小。本文提出的四谱线插值算法，在对电网中谐波的幅值与相位检测上与已知的双谱线插值算法与三谱线插值算法相比，具有更高的检测精度。基于四谱线插值算法，文中给出了常用窗函数对应的修正公式。通过仿真分析，显示了该算法在高精度分析谐波成分时具有较好的实用价值。

[1] JAIN V K, COLLINS W L. High-accuracy analog measurements via interpolated FFT[J]. IEEE Trans on Instrumentation and Measurement, 1979, 28(2): 113-122.

[2] MARANO S, MATTA V, WILLETT P. Sequential detection of almost-harmonic signals[J]. IEEE Trans on Signal Processing, 2003, 51(2): 395-405.

[3] HIDALGO R M, FERNANDEZ J G, RIVERA R R, et al. A simple adjustable window algorithm to improve FFT measurements[J]. IEEE Trans on Instrumentation and Measurement, 2002, 51(1): 31-36.

[4] 王刘旺, 黄建才, 孙建新, 等. 基于加汉宁窗的FFT高精度谐波检测改进算法[J]. 电力系统保护与控制, 2012, 40(24): 28-33.

WANG Liu-wang, HUANG Jian-cai, SUN Jian-xin, et al. An improved precise algorithm for harmonic analysis based on Hanning-windowed FFT[J]. Power System Protection and Control, 2012, 40(24): 28-33.

[5] 庞浩, 李东霞, 俎云霄, 等. 应用FFT进行电力系统谐波分析的改进算法[J]. 中国电机工程学报, 2003, 23(6): 49-54.

PANG Hao, LI Dong-xia, ZU Yun-xiao, et al. An improved algorithm for harmonic analysis of power system using FFT technique[J]. Proceedings of the CSEE, 2003, 23(6): 49-54.

[6] AKAGI H. New trends in active filters for power conditioning[J]. IEEE Trans on Industry Applications, 1996, 32(6): 1312-1322.

[7] 耿涛, 赵金. 改进低通滤波器的瞬时无功功率谐波电流检测方法[J]. 电力系统保护与控制, 2009, 37(6): 53-56.

GENG Tao, ZHAO Jin. Instantaneous reactive power theory harmonic detection method based on improved lowpass filter[J]. Power System Protection and Control, 2009, 37(6): 53-56.

[8] 陆秀令, 周腊吾. 基于瞬时无功功率的谐波电压检测法[J]. 高电压技术, 2006, 32(1): 88-90.

LU Xiu-ling, ZHOU La-wu. Detecting method of harmonic voltage based on instantaneous reactive power theory[J]. High Voltage Engineering, 2006, 32(1): 88-90.

[9] 周福林, 李群湛, 解绍峰, 等. 无锁相环单相无功谐波电流实时检测方法[J]. 电工技术学报, 2010, 25(1): 178-182.

ZHOU Fu-lin, LI Qun-zhan, XIE Shao-feng, et al. Real time detecting method for single-phase reactive and harmonics currents detection without PLL[J]. Transactions of China Electrotechnical Society, 2010, 25(1): 178-182.

[10] CHANG G W, CHEN C I, TENG Y F. Radial-basis- function-based neural network for harmonic detection[J]. IEEE Trans on Industrial Electronics, 2010, 57(6): 2171-2179.

[11] 侯世英, 汪瑶, 祝石厚. 遗传算法改进神经网络的电力系统谐波检测法[J]. 重庆大学学报, 2008, 31(5): 491-494.

HOU Shi-ying, WANG Yao, ZHU Shi-hou. A harmonic measuring approach based on genetic algorithm improved back-propagation neural network[J]. Journal of Chongqing University, 2008, 31(5): 491-494.

[12]王凯亮, 曾江, 王克英. 一种基于BP神经网络的谐波检测方案[J]. 电力系统保护与控制, 2013, 41(17): 44-48.

WANG Kai-liang, ZENG Jiang, WANG Ke-ying. A harmonic detecting scheme based on BP neural network[J]. Power System protection and Control, 2013, 41(17): 44-48.

[13] 兰华, 李龙飞, 王韵然, 等. 改进单峰谱线插值算法在谐波检测中的应用[J]. 东北电力大学学报, 2009, 29(4): 26-29.

LAN Hua, LI Long-fei, WANG Yun-ran, et al. An application in harmonic detection using an improved single-spectral-line interpolation algorithm[J]. Journal of Northeast Dianli University, 2009, 29(4): 26-29.

[14] 高云鹏, 腾召胜, 卿柏元. 基于Kaiser窗双谱线插值FFT的谐波分析方法[J]. 仪器仪表学报, 2010, 31(2): 287-292.

GAO Yun-peng, TENG Zhao-sheng, QING Bai-yuan. Harmonic analysis based on Kaiser window double spectrum line interpolation FFT[J]. Chinese Journal of Scientific Instrument, 2010, 31(2): 287-292.

[15] 李绍铭, 纪萍, 彭玉龙. 基于加窗插值FFT和动态频率的谐波检测算法[J]. 自动化与仪器仪表, 2009(3): 93-95.

LI Shao-ming, JI Ping, PENG Yu-long. Harmonic detection method based on interpolation FFT window and dynamic frequency[J]. Automation & Instrumentation, 2009(3): 93-95.

[16]曾博, 滕邵胜, 高云鹏, 等. 基于Rife-Vincent窗的高准确度电力谐波相量计算方法[J]. 电工技术学报, 2009, 24(8): 154-159.

ZENG Bo, TENG Zhao-sheng, GAO Yun-peng, et al. An accurate approach for power harmonic phasor calculation based on Rife-Vincent window[J]. Transactions of China Electrotechnical Society, 2009, 24(8): 154-159.

[17] 龚仁喜, 周希松, 宁存岱, 等. 基于LabVIEW的FFT加窗插值算法在谐波检测中的应用[J]. 重庆理工大学学报: 自然科学, 2010, 24(5): 64-70.

GONG Ren-xi, ZHOU Xi-song, NING Cun-dai, et al. Windowed interpolation algorithm in FFT for harmonics detection based on LabVIEW[J]. Journal of Chongqing University of Technology: Natural Science, 2010, 24(5): 64-70.

[18]王继东, 杜旭浩, 杨帆. 基于三次样条插值信号重构的微网谐波及间谐波分析算法[J]. 电网技术, 2012, 36(11): 7-11.

WANG Ji-dong, DU Xu-hao, YANG Fan. A cubic spine interpolation signal reconstruction-based harmonic and iner-harmonic analysis algorithm for microgrid[J]. Power System Technology, 2012, 36(11): 7-11.

[19]杨晓萍, 刘普森, 钟彦儒. 基于经验模式分解的有源滤波器谐波检测[J]. 电工技术学报, 2009, 24(5): 197-202.

YANG Xiao-ping, LIU Pu-sen, ZHONG Yan-ru. Harmonic detection of active power filter based on empirical mode decomposition[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 197-202.

[20]牛胜锁, 梁志瑞, 张建华, 等. 基于三谱线插值FFT的电力谐波分析算法[J]. 中国电机工程学报, 2012, 32(16): 130-136.

NIU Sheng-suo, LIANG Zhi-rui, ZHANG Jian-hua, et al. An algorithm for electrical harmonic analysis based on triple-spectrum-line interpolation FFT[J]. Proceedings of the CSEE, 2012, 32(16): 130-136.

A power network harmonic detection method based on the four-spectrum-line interpolation FFT

HAO Zhu, GU Wei, CHU Jian-xin, MA Zhao

(Marine Technology and Control Engineering Key Laboratory of Transportation Ministry, Shanghai Maritime University,Shanghai 201306, China)

When the Fast Fourier Transform (FFT) method is used to analyze the harmonics in a power network, the sampled signal’s non-integral period truncation and non-synchronous sampling can cause the spectrum leakage, which will affect the accuracy of the detective results. In order to improve the accuracy of the harmonic detection, this paper puts forward a Fast Fourier Transform algorithm based on four-spectrum-line interpolation algorithm. Through analyzing the adding window signal amplitude information at the discrete frequency points, the algorithm further enhances the accuracy of the amplitude and phase detection by using weighted arithmetic of four pillars spectral line near the harmonic frequency point. By data fitting, practical correction formulas corresponding to commonly used window functions are obtained. Through numerical simulation analysis, it can be seen that the algorithm has higher detection accuracy. The accuracy and effectiveness of the algorithm is verified by the results of the simulation.

four-spectrum-line interpolation; FFT; harmonic detection; window function; data fitting

TM714

A

1674-3415(2014)19-0107-07

2013-12-09；

2014-02-25

郝 柱（1987-），男，硕士研究生，从事船舶、港口及自动化技术研究；E-mail: hz06022094@126.com

顾 伟（1957-），男，教授，博导，主要研究方向为港口、船舶自动控制技术；

褚建新（1955-），男，教授，博导，主要研究方向为电气传动及自动化技术。

省部级项目“船舶电力推进系统故障诊断与安全控制技术研究及应用”(11170501700)