某火箭炮托架结构的优化设计与研究

卢云，张龙

(南京理工大学 机械工程学院，江苏 南京 210094)

0 前言

在战场上战士往往需要背负沉重的武器装备，为了提高整个部队的机动能力，光凭提高战士的个人能力是远远不够的，武器轻量化技术不仅可以显著提高作战部队的机动能力，而且还可以降低武器装备的制造成本。通常情况下，火箭炮的攻击力越强其自身质量也就越大，目前有两种方法可以减轻火箭炮的总质量：1) 使用先进的轻型材料，2) 利用科学合理的方法对结构进行优化设计[1]。托架在火箭炮整体结构当中所占比重较大，同时也是支撑耳轴和安装定向器的重要部件。因此，对托架结构进行优化设计是火箭炮研究工作中的一个重要组成部分[2]。

本文运用多学科多目标优化软件Isight集成SolidWorks三维设计软件和Abaqus有限元分析软件，采用有效的实验设计、近似模型和优化方法，实现了对复杂机械装配体结构的全自动仿真与优化的一体化流程，为典型机械结构的轻量化提供了一种有效的研究方法。

1 托架参数化结构有限元分析

1.1 参数化结构模型

该火箭炮托架主要由左、右、后支撑板、底盘、四根上横梁、四根下横梁和四根纵梁组成。由于在有限元分析软件中建模较为复杂，故选用SolidWorks三维建模软件对托架进行参数化建模，其结构实体模型如图1所示。

图1 托架结构实体模型

1.2 有限元模型的建立

托架结构的材料统一选择45号钢，密度为7.8e-9t/mm3，弹性模量E=2.06e5MPa，泊松比为0.3，屈服极限为355MPa。

火箭炮有多种发射状态，现仅考虑高低射角和方向射角都为0°且两发齐射的发射状态。对底盘采用全约束，对各接触面采用焊接接触，将火箭炮满载时的质量施加到托架质心的参考点上，将水平发射状态的冲击力分别施加到托架耳轴的两个参考点上。

在将模型导入Abaqus之前，对模型进行简化处理，忽略一些微小的倒角，用光滑的圆孔代替螺纹孔，从而提高计算效率[3]。全模型采用六面体网格，单元类型为C3D8R，单元总数为38274，节点总数为67793。

1.3 有限元分析结果

经Abaqus分析后，模型的最大应力值为52.06MPa，出现在底盘与下横梁的接触附近位置，如图2所示，其值远远小于屈服极限355MPa，最小安全系数达到了6.82，大于强度评判标准2.5，并测得托架的净重为26.31kg，有必要对其进行轻量化设计。

图2 托架应力云图

2 托架结构的优化设计

2.1 实验设计方法的选用

以轻量化为设计目标，以火箭炮托架的总质量最小为目标函数，将安全屈服极限作为优化的约束条件，设计变量为各梁的厚度t1～t12、支撑板厚度t13～t15和底盘的厚度t16，为了提高优化效率，可以先用实验设计方法对设计变量进行精选，并调整设计空间。典型有效的试验设计方法有：正交试验设计、拉丁超立方设计和最优拉丁超立方设计[4]。其中最优拉丁超立方设计具有较好的空间填充性和均衡性，能够较为均匀地布置样本点[5-6]。为了获得更好的优化方案，首先通过最优拉丁超立方设计初估最优值，然后以最优点为中心在其附近补充采样点，形成中心处较密，越往外越疏的实验方法，共采样100次，经分析后其Pareto图如图3所示。

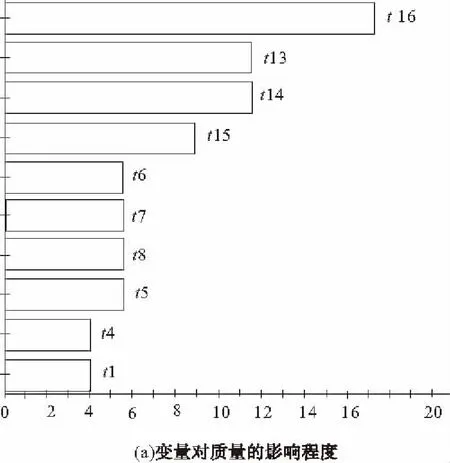
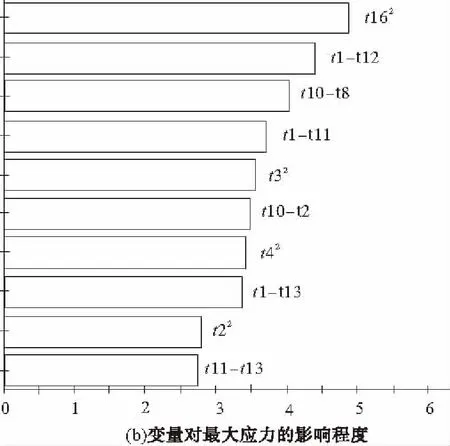
图3 实验设计Pateto图

从Pareto图中可以直观地看出各设计变量对质量和最大应力的影响程度，其中t13～t16，t5～t8对质量影响程度较大，t2～t4，t16的二阶效应以及一些变量的交互效应(如t1与t12)对最大应力影响程度较大，通过综合对比与分析，选取四根纵梁(t5～t8)、三根上横梁(t1，t4，t10)、四根下横梁(t2，t3，t11，t122)以及左右后支撑板(t132，t142，t15)和底盘(t162)为最终的设计变量。其中横纵梁采用方形冷弯空心型钢，此钢有固定规格的厚度尺寸，建立如表1所示的设计变量参数。

表1 设计变量参数

2.2 近似模型的建立

由于火箭炮托架结构较为复杂，运行一次的建模和仿真时间较长，在Isight中还需要多次调用SolidWorks和Abaqus进行建模与分析，采用近似模型方法替代原始模型可以显著提高优化效率，缩短计算时间。近似模型的构建方法有多种，主要包括：响应面法、Kriging方法和神经网络技术[7]。为了能够得到精确的近似模型，本文采用改进的EBF(elliptical basis functions)神经网络技术。EBF神经网络与RBF神经网络结构相似，同样是含有隐层的三层前馈神经网络，可以将它看做是RBF神经网络的扩展[8]。传统EBF神经网络的输出层函数形式为：

(1)

取马氏距离作为基函数，其表达式为：

(2)

激活函数通常采用高斯函数，其表达式为：

(3)

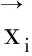
为了可以高精度地逼近原始模型，采用可变次数的样条椭球基函数作为激活函数，其表达式为：

(4)

其中：

S≈diag(si)

(5)

(6)

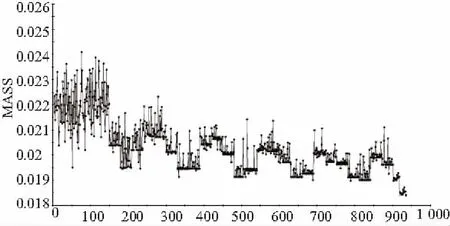
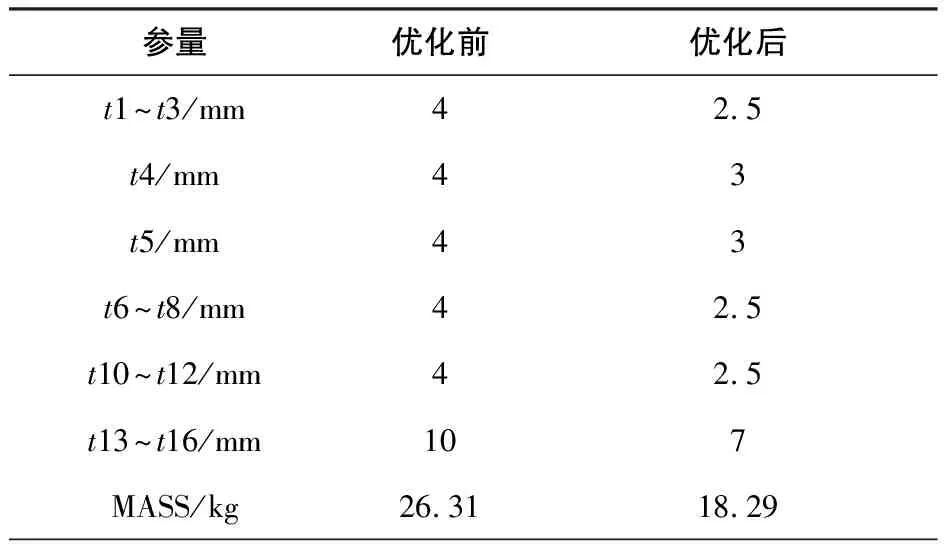
式中，c为形函数变量(0.2

2.3 优化分析

在近似模型的基础之上，对结构进行优化分析，采用多岛遗传算法和序列二次规划法的组合优化策略，充分利用全局算法的空间遍历能力和梯度算法的高效寻优能力。在多岛遗传算法中设定种群数为30，岛数为3，代数为10，共进行30×3×10=900次迭代，序列二次规划法的最大迭代次数为50。当多岛遗传算法计算完成后，序列二次规划法会自动将多岛遗传算法得到的最优解作为初始值再次进行寻优，最终实现从全局到局部的优化。

如图4所示，从质量优化历程图中可以看到整个寻优过程呈逐渐下降趋势，在前900次迭代中处于全局探索阶段，收敛较慢，后33次迭代中处于局部寻优阶段，能够精准快速地找到最优解。经过优化分析后，火箭炮托架结构质量变为18.29kg，与优化前质量相比，减少了30%，达到了轻量化目标，运用近似模型优化前后各参量变化如表2所示。

图4 基于EBF模型的托架Mass优化历程

参量优化前优化后t1～t3/mm42.5t4/mm43t5/mm43t6～t8/mm42.5t10～t12/mm42.5t13～t16/mm107MASS/kg26.3118.29

续表2

maxMises/MPa52.0683.56安全系数6.824.25

图5为优化后用Abaqus对火箭炮托架进行有限元分析的应力云图，从图中可以看出最大应力依旧出现在底盘与下横梁的接触附近位置，最大应力为84.31MPa，此值与运用近似模型优化得到的最大应力值83.56MPa非常接近，充分表明运用的EBF神经网络技术所构造的近似模型具有较高精度。优化后经计算安全系数为4.25，仍然是一个保险安全的设计，满足设计要求。

图5 优化后托架应力云图

3 结论

对某火箭炮托架结构进行了有限元分析，通过仿真分析结果建立了相应的优化模型，在Isight中构建了SolidWorks和Abaqus的仿真与优化一体化环境。所提出的试验设计、近似模型和组合优化方法提高了优化的寻优能力，使火箭炮托架结构质量从26.31kg减少到了18.29kg，虽应力有所增加，但依然满足安全设计要求，这些分析结果对其他典型机械结构的轻量化研究具有一定的参考意义。

[1] 韩志强.某发射装置上架的减重技术研究 [D].南京：南京理工大学，2006.

[2] 高明坤，宁廷伦.火箭导弹发射装置设计 [M].北京：北京理工大学出版社，1998.

[3] 曹金凤，石亦平.ABAQUS有限元分析常见问题解答 [M].北京：机械工业出版社，2009.

[4] 刘文卿.试验设计 [M].北京：清华大学出版社，2005.

[5] 刘晓路，陈英武，荆显荣，等.优化拉丁方试验设计方法及其应用 [J].国防科技大学学报，2011，33(5) ：73-77.

[6] ZHAO Min，CUI Weicheng.Application of the optimal Latin hpercube design and radial basis function network to collaborative optimization[J].Journal of Marine Science and Application，2007，6(3)：24-30.

[7] 姜超，邵志良.近似模型方法在复杂结构优化设计问题中的应用 [J].上海汽车，2010(9)：44-47.

[8] 邢红杰，王泳，胡包钢.椭球基函数神经网络的混合学习算法 [J].模式识别与人工智能，2008(21)2：148-154.