六轮车辆滑移转向动力学建模和运动特性分析

2014-08-16杨闫景钱瑞明

机械制造与自动化 2014年3期

杨闫景，钱瑞明

(1.93511部队，山西代县 034200；2.东南大学机械工程学院，江苏南京 211189)

0 前言

滑移转向即为差速转向，通过控制车辆左右两侧各车轮的方向和转速大小从而达到车辆转向的目的。

轮式滑移转向车辆因其结构简单、运动灵活、控制方便等优点，所以在工业生产、科考、交通等诸多领域被广泛的应用。目前文献[1,2]对轮式滑移转向大多以“车轮切向力和轴向力独立求解”为基础进行分析，模型比较复杂，且主要以四轮车辆为例进行分析[3]。本文基于车轮触地点的速度分析、轮轴转动副摩擦分析和车辆力平衡关系，对一种六轮车辆稳态滑移转向过程进行动力学建模，并研究车轮转速和车辆主要结构参数对滑移转向特性的影响关系。

1 滑移转向动力学模型的建立

图1为一种六轮车辆匀速绕转动中心C作滑移右转向的状态，随车坐标系xoy原点取为车辆两后轮中心连线的中点，设车轮与地面间为有摩擦点接触。车辆滑移转向参数如图1所示，第i车轮转速为ωi(俯视向前旋转为正，左侧转速大于右侧转速)，车轮半径均为R，第i个车轮中心Oi的坐标为(xi,yi)，转动瞬心C坐标为(xC,yC)，车辆稳态转向角速度为ω(顺时针方向，为正)，COi与x轴的夹角为αi(本文所有夹角均由x轴正向沿逆时针方向度量)，COi的长度为L(Oi,C)。

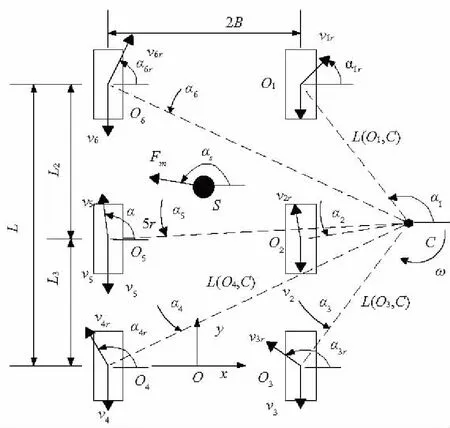
图1 六轮车辆滑移转向分析模型

第i车轮上触地点相对于车体的速度为vi=Rωi，第i车轮中心Oi相对地面的绝对速度为vir=L(Oi,C)ω，其方向垂直于COi，αir为vir与x轴的夹角，如图1。车轮触地点相对地面的绝对速度vid为vi和vir的合成，vid与x轴的夹角为αid，见图2。

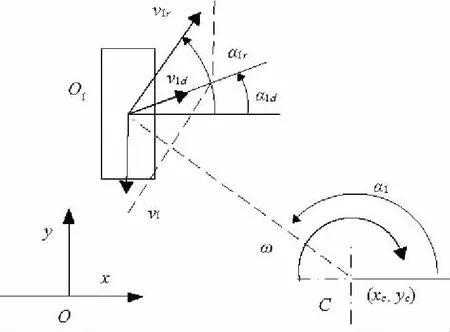
图2 轮1速度分析

以车轮1为例，对其进行速度分析，可得：

(1)

tanα1=(y1-yC)/(x1-xC)。

由图2可知，α1d位于第一象限，整理式(1)可得：

(2)

触地点处的滑动摩擦力方向与滑动速度方向相反，即轮1上触地点处滑动摩擦力与x轴夹角为α1f=α1d+π。同理根据αid所在象限即可求得其余车轮摩擦力方向角αif。

(3)

设车辆总质量为m，质心S坐标为(xS,yS)，质心瞬时转动半径为r，则车辆转向时的离心力为(xs,ys，离心力方向角度为αS。则可得匀速转向时的车辆动力学方程为：

(4)

式中：摩擦力Ffi=μNi；Ni为地面对第i个车轮正压力，μ为车轮与地面间的滑动摩擦系数(设为定值)。

2 轮轴转动副摩擦力矩分析

轮式车辆滑移转向过程中，轮轴转动副因受到较大的轴向力和径向力，导致转动副摩擦力矩对车辆所需转向力矩影响较大。转动副Adams模型[4]如图3，图3(a)为转动副剖视图，图3(b)为局部侧视图。

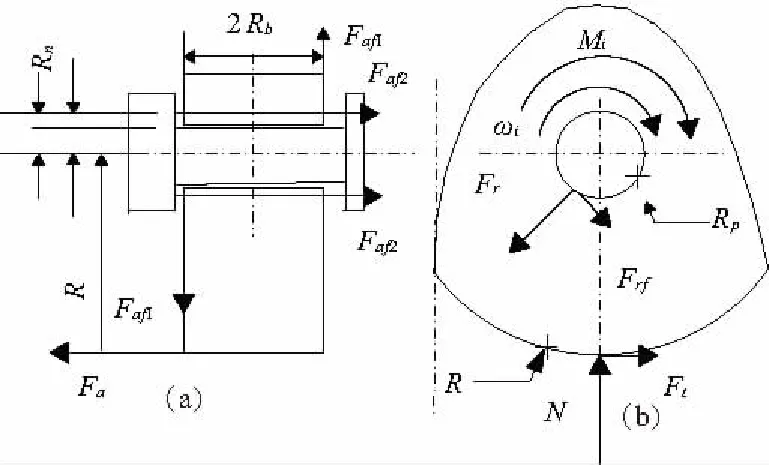
图3 转动副adams力学模型

车轮受摩擦力Ff和正压力N作用，从而使车轮与轴之间存在着转动副摩擦力矩。若将Ff的分解为轴向分力Fa和切向分力Ft，则因Fa对车轮形成翻转力矩，车轮孔与轴之间形成反作用力Faf1；因Fa使车轮与轴端面间挤压形成反作用力Faf2；Ft和N使轴对车轮形成径向压力Fr。设Faf1和Faf2形成摩擦力矩Mfa，Ft形成Mft，即：

(5)

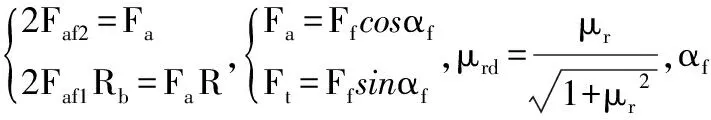
由式(4)、(5)可知第i个轮所需力矩为：

Mi=±|μNisinαifR|+Mfi

(6)

式中：Mfi=Mfai+Mfti，当车轮转向和Ft所产生的摩擦力矩方向相同时绝对值符号前取负号，否则取正号[5]。

概括而言，滑移右转向中，当不考虑转动副摩擦时，两侧车轮所需力矩相同；否则：两侧车轮转向相同时，则左侧所需力矩大、为驱动力矩，右侧为制动力矩；两侧车轮转向相反时，则两侧车轮所需力矩相同，且均为驱动力矩。

3 车辆参数对转向的影响

3.1 左右侧车轮转速比对转向的影响

六轮车辆参数如表1，其中假定地面对每个车轮正压力Ni相等。当左侧车轮转速ωl为16.7r/min，右侧车轮转速ωr与左侧车轮转速ωl之比i=ωr/ωl由-1至0.8变化时，将表1各项参数代入式(3)、(4)，利用matlab可求解出车辆匀速滑移转向时的转动瞬心C坐标和转向角速度ω，以及各摩擦力角度αif的数值解。图4为i=-1时摩擦力角度示意图，转向参数为(xC,yC)=(0,0.0769)m，ω= 3.86r/min。滑移转向参数变化情况如图5。图5(a)为车轮1摩擦力角度，变化范围极小；图5(b)为转动瞬心x坐标，呈指数上升，当右侧车轮转速为0时，xc>B；图5(c)为转动瞬心y坐标，变化范围极小，当右侧车轮转速为0时，瞬心y坐标最大；图5(d)为车辆转向角速度ω，其与右侧和左侧车轮转速比i呈等比关系。

表1 六轮车辆原始参数

图4 各车轮所受摩擦力角度示意

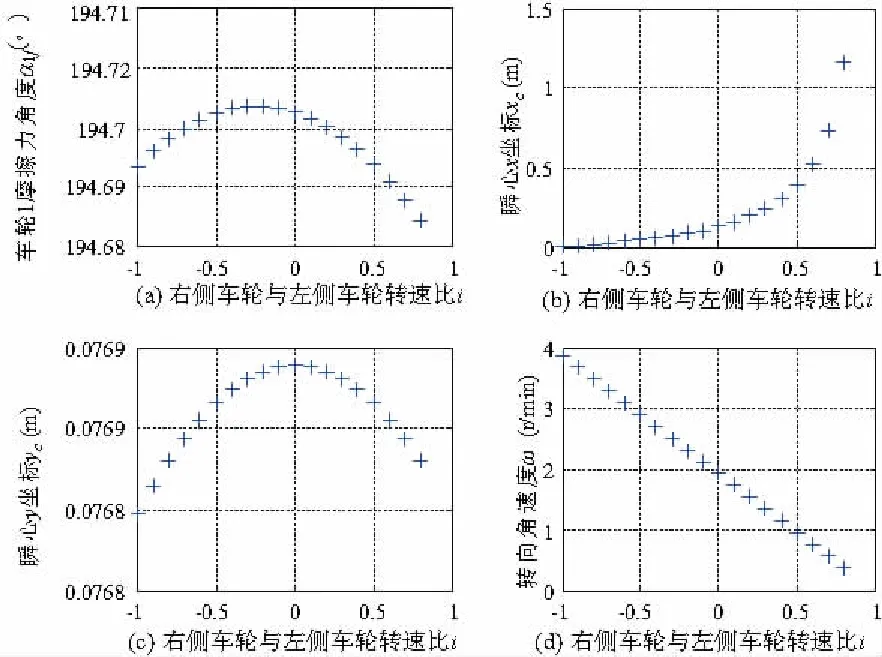
图5 右侧车轮与左侧车轮转速比对转向影响

同时研究表明瞬心坐标和摩擦力角度与离心力有较大的关系，当忽略离心力，且左侧和右侧车轮转速分别相等时，摩擦力角度仅与车辆几何尺寸和质心位置有关。

3.2 轴距和轮距对转向的影响

车辆轴距和轮距对滑移转向影响甚大。设六轮车辆左侧与右侧车轮转速相等，方向相反，ωl=-ωr=16.7r/min。

当轮距2B=0.21m，中间组车轮y坐标L3由0至0.17m变化时，车辆滑移转向参数变化情况如图6。图6(a)为右侧车轮所需力矩Mr，上曲线为理论所需力矩，下曲线为考虑转动副摩擦时所需力矩；图6(b)为转动瞬心x坐标，变化范围小于1mm；图6(c)为转动瞬心y坐标，与L3近似等比变化；图6(d)为车辆转向角速度ω，与L3呈U型关系。可以看出当中间组车轮y坐标L3=L/2时，所需力矩Mr最小，但转向角速度ω亦最小。

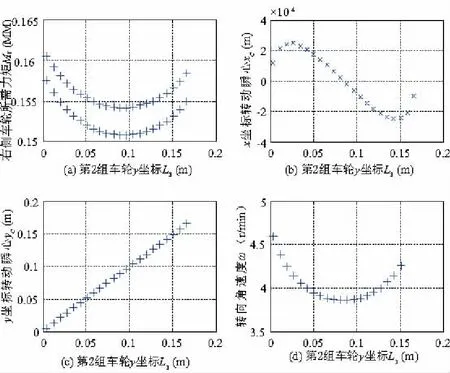
图6 轴距对车辆滑移转向影响

当中间组车轮轮距2B由0至0.4m变化、y坐标为L3=L/2时，车辆滑移转向参数变化情况如图7(a)为右侧车轮所需力矩Mr，上曲线为考虑转动副摩擦时所需力矩，下曲线为理论所需力矩，Mr与轮距呈等比变化；图7(b)和图7(c)分别表明转动瞬心x、y坐标固定不变；图7(d)为车辆转向角速度ω，与轮距近似等比变化关系。