弧齿锥齿轮四阶传动误差的设计*

苏进展 方宗德 蔡香伟

(1.长安大学 道路施工技术与装备教育部重点实验室，陕西 西安 710064;2.西北工业大学 机电学院，陕西 西安 710072)

传动误差是由齿面非共轭特性和啮合刚度变化的共同作用产生的，它包括动态性能和强度状况等信息.大量的理论研究和试验已经充分证明了传动误差对动态特性有直接的影响.国内外学者通过优化设计、高重合度设计、修形等方法来改善弧齿锥齿轮的啮合特性［1-5］.但传统的二阶抛物线传动误差在啮入和啮出时的一阶导数符号是相反的，易引起齿对间的振动和冲击，并削弱齿根强度.Stadtfled［6］研究了螺旋锥齿轮高阶传动误差，并验证了其能降低齿轮副的振动和噪声.Wang 等［7-8］通过修改小轮径向刀位的方法来实现四阶传动误差曲线.魏冰阳等［9］提出了基于高阶变性法的螺旋锥齿轮高阶传动误差设计方法，以改善齿轮副的啮合性能.Lee［10］提出了四阶传动误差的圆柱齿轮修形方法，以提高齿根强度和降低齿轮副的振动噪声.盛钢等［11］提出了斜齿轮四阶传动误差的设计方法，以降低误差敏感性.笔者提出了预置四阶传动误差曲线，以改善圆弧齿圆柱齿轮的啮合稳定性和齿根强度［12］.

鉴于二阶抛物线传动误差在改善齿轮动力学特性方面存在的不足，以及现阶段对高阶传动误差的设计原理及减振降噪机理缺乏深入的研究，文中提出了一种预置重合度的传动误差设计方法，以满足齿轮副设计重合度和位置对称性要求，并预置四阶传动误差表达式，通过几何约束方程求解其系数，结合传动误差定义获得大轮和小轮啮合转角的关系式，再由逆轮齿接触分析(TCA)方法反求滚比多项式系数，最后借助轮齿承载接触分析(LTCA)［13］和齿面相对修形图对具有四阶传动误差的弧齿锥齿轮进行比较和分析.

1 对称传动误差的设计

理想的传动误差曲线是形状中凸、相邻齿对相交的曲线.采用基于局部综合法［14］或局部共轭原理设计的齿轮副，经常出现传动误差开口过大或过小甚至反向，形状整体歪斜或左右不对称以及发生S型畸变等缺陷，无法实现预置的啮合传动性能.对称传动误差是指以设计参考点为对称中心，啮入、啮出点的幅值和啮入、啮出时间相等，且曲线形状完全对称.图1 为局部综合法设计参数示意图，包括接触迹线方向角η2和设计参考点M0位置.

啮入、啮出位置关于点M0对称的设计流程如图2 所示，首先讨论给定设计重合度下啮入和啮出时间相等的传动误差设计，具体步骤如下:

图1 局部综合参数示意图Fig.1 Sketch of local synthesis parameters

(1)给定参考点M0的局部综合参数，通过主动设计获得小轮机床加工参数［15］.

(2)由TCA 和大轮齿顶、小轮齿顶啮合的几何条件计算出啮入位置Tin和Tout，M0的啮合位置T0由局部综合法直接算出.

(4)定义设计重合度εr为主动轮轮单齿从进入啮合到退出啮合的总啮合时间和啮合周期Tmesh的比值.若由TCA 得到的εr小于或大于预定的设计重合度ε0，则可以减小或增大接触迹线的方向角η2.

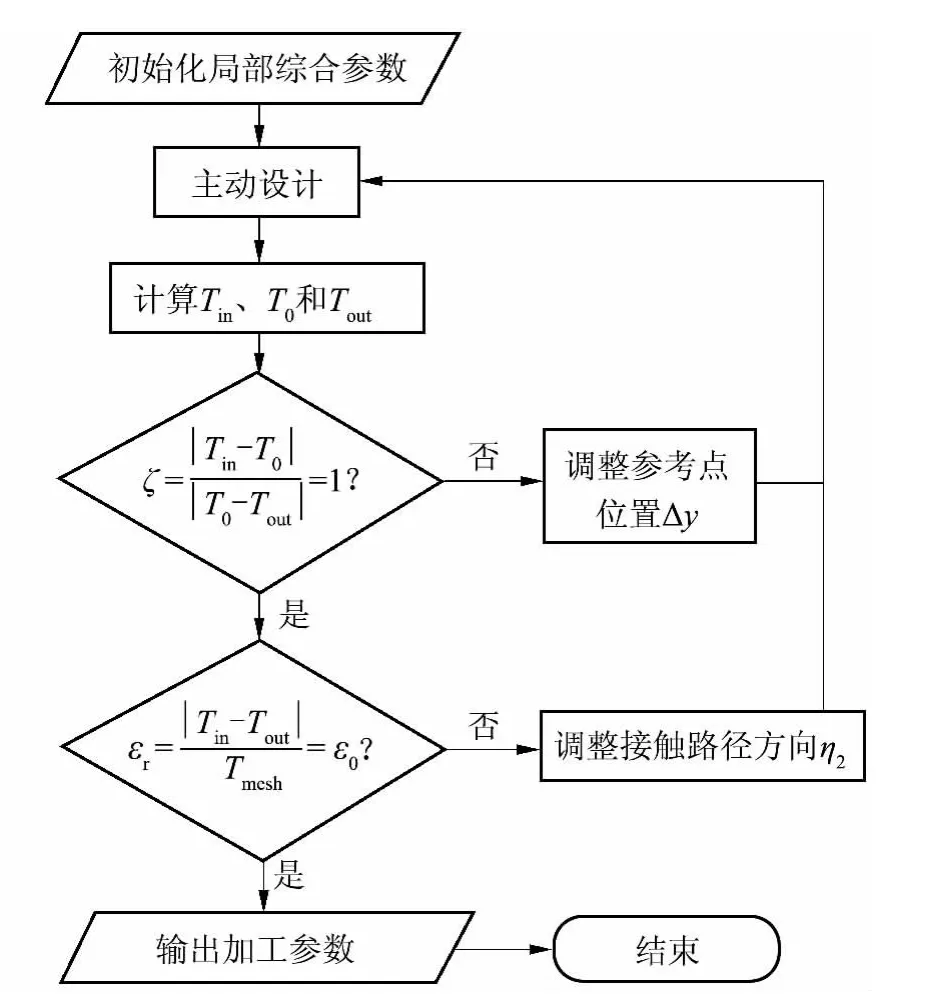
图2 位置对称性设计流程图Fig.2 Flowchart of position symmetry design

2 四阶抛物线传动误差的设计原理

由局部综合法和主动设计所得到的传动误差近似为二阶抛物线传动误差.抛物线传动误差具有稳定的啮合传动性能，能够吸收由安装误差产生的线性误差，经过合理设计可以满足航空弧齿锥齿轮的高强度、低噪声要求.二阶抛物线传动误差的系数ap通过啮合转换点的幅值或者啮入、啮出点幅值就可以求出.在设计重合度相同的条件下，啮合转换点和啮入、啮出点的传动误差均随抛物线系数ap的增大而增大;虽然ap的增大可以避免重载下过早出现边缘接触，但在轻载、中载工况下的承载传动误差波动会增大，从而引起传动系统较大的振动与噪声.啮合转换点处的传动误差幅值会影响齿轮副轻载下的振动特性及承载传动误差最小波动量对应的载荷.图3 所示为二阶和四阶抛物线传动误差示意图，其中二阶抛物线传动误差的啮入、啮出位置及幅值是对称的.

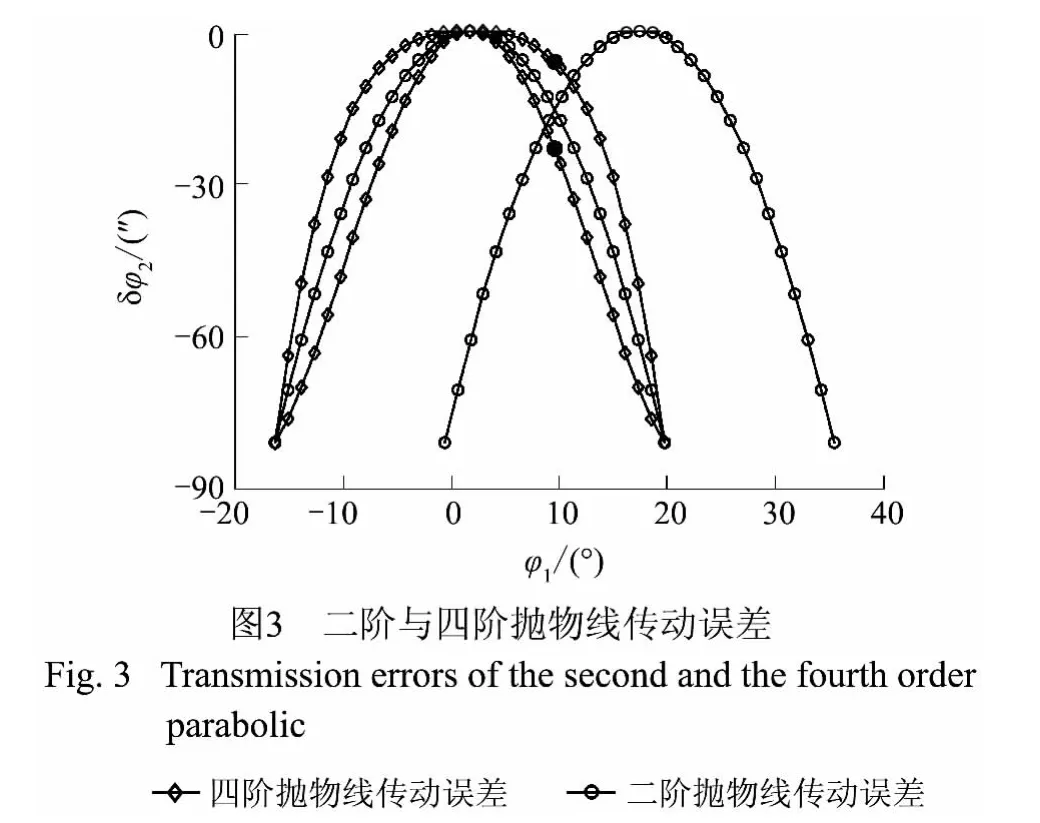
在此基础上，文中提出了设计重合度和啮入、啮出点幅值均与二阶对称抛物线传动误差相同，但能够根据不同需求调整啮合转换点幅值的弧齿锥齿轮四阶抛物线传动误差的设计方法.四阶抛物线传动误差是由四次项和二次项组成，其表达式为

(1)啮合转换点T0－0.5Tmesh处的传动误差幅值可以根据安装误差条件下避免出现边缘接触和实际工况载荷下承载传动误差波动量最小来确定，即

式(2)和(3)可以写成线性方程组的形式

求解上述线性方程，即可确定系数a 和b.

从前面分析可知，式(2)保证了啮合转换点的传动误差幅值可根据不同需求进行调整.而式(3)满足了四阶抛物线传动误差在啮入或啮出点的幅值与抛物线传动误差幅值相等的条件，保证原有的设计重合度.

3 四阶抛物线传动误差的实现

传动误差的表达式为

式中，φ1、φ2分别为小轮和大轮的实际转角，N1、N2分别为小轮和大轮的齿数，和分别为小轮和大轮的初始转角.根据传动误差的定义和预置四阶抛物线传动误差，可求出大轮实际啮合转角:

式(6)为小轮啮合转角φ1和大轮啮合转角φ2的约束方程.当φ1和φ2按照式(6)规律传动时，就能够得到预置的四阶抛物线传动误差.

图4 为弧齿锥齿轮TCA 坐标系，包括小轮坐标系S1、大轮坐标系S2、固定坐标系Sh.在Sh坐标系下的TCA 基本方程组为

图4 齿轮副的啮合坐标系Fig.4 Fixed coordinate system for meshing gear drive

TCA 是在已知大、小轮齿面方程的条件下进行的，文中是在已知四阶抛物线传动误差δφ2和大轮齿面r2(θg，φg)下，通过逆TCA 来确定小轮齿面方程.具体求解思路如下:给定一个φ1，根据式(6)求得φ2，两者是一一对应关系;采用变性法实现预置四阶抛物线传动误差加工，即计算出小轮产形轮和被加工小轮的瞬时滚比Rap;保持大轮齿面原有的几何特性不变，仅对小轮齿面进行修正.将(见式(7))中的Rap用产形轮转角φc(摇台转角)和小轮加工转角φp来代替，于是，式(7)中仍包含有6个未知数(θp，θg，φp，φg，φc，φ1，φ2(φ1))，取φ1为自变量，求解新方程组.

根据预置四阶抛物线传动误差的表达式，齿轮副从进入啮合到退出啮合按照一定步长得到一系列(φ1i，φ2i)，将其代入TCA 方程组(7)可求出一系列的(φp，φc)值.把(φp，φc)回归成如下的多项式形式:用逆TCA 方法可得到实现四阶抛物线传动误差的滚比修正系数.将式(8)代入小轮齿面方程，就可以获得具有四阶抛物线传动误差的小轮齿面.从四阶抛物线传动误差的设计原理可知，实现这种类型的传动误差仅需调整变性系数，其他机床调整参数保持不变.

4 算例分析

用算例来说明文中设计方法，并对5 种四阶传动误差的多载荷承载传动误差进行比较分析.弧齿锥齿轮的基本参数如表1 所示，表2 列出了5 种四阶抛物线传动误差的相关系数，包括四阶抛物线系数(a，b)、啮合转换点幅值δφ(Tp)2、滚比多项式系数(c0，c1，c2，c3).TCA 结果(包括传动误差和齿面印痕)如图5 所示.

表1 弧齿锥齿轮副几何参数Table 1 Geometric parameters of gear blank

表2 四阶抛物线传动误差系数Table 2 Coefficients of transmission errors of the fourth order parabolic

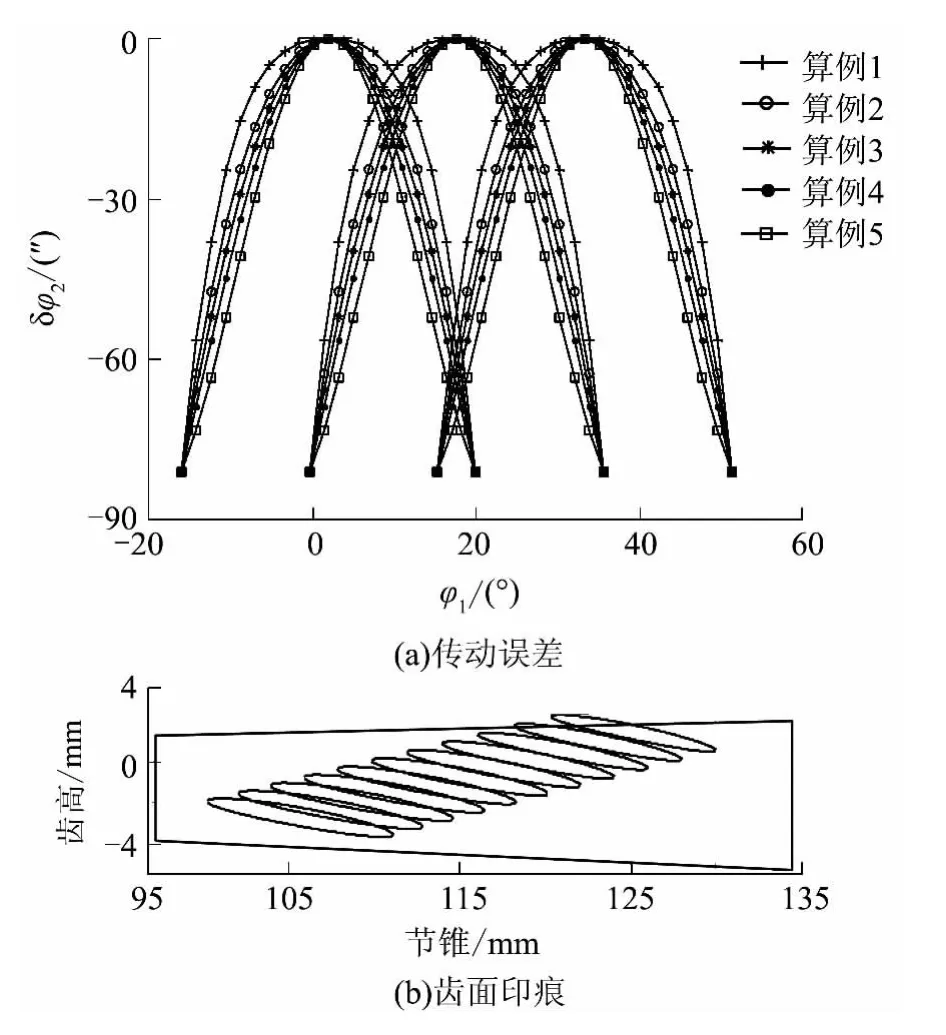
图5 四阶抛物线的传动误差和齿面印痕Fig.5 Transmission errors and contact patterns of the fourth order parabolic

利用LTCA 分别对算例1、3、5 在多载荷工况下的承载传动误差进行分析，结果如图6 所示.从图可知:算例1 啮合转换点的幅值较二阶抛物线传动误差的幅值小，在轻载工况(0～300 Nm)下，承载传动误差的波动量均比算例3 和5 小，最小波动量出现在100～300 Nm 之间，当扭矩从400 Nm 到1 000 Nm变化时，波动量逐渐增大;算例5 啮合转换点的幅值较二阶抛物线传动误差的幅值大，当输出扭矩小于300 Nm 时，承载传动误差的波动较大，而当扭矩从400 Nm 变化到1 000 Nm 时，波动量先减小后增大，最小波动量出现在扭矩为600～800 Nm 之间，这表明四阶抛物线传动误差使齿轮副在轻载条件下的波动量有所增大，且改变了出现最小波动量的扭矩(图6(a)中为400 Nm)，同时也保证了齿轮副在最大扭矩为1000 Nm 时不出现边缘接触.

图7 为算例1、3、5 相对于与大轮共轭齿面的小轮齿面的偏差图.齿面中部的相对修形量(Ease-off)从小到大排序依次是算例1、算例3、算例5，这是由四阶抛物线传动误差在参考点附近的平缓程度来决定的.另外，算例1 的四阶传动误差的中部平缓、两端较陡，有利于降低啮合印痕对安装误差的敏感性.

5 结论

文中提出了预置重合度的弧齿锥齿轮四阶抛物线传动误差设计方法，得出如下结论:

图6 算例1、3、5 的多载荷承载传动误差比较Fig.6 Comparison of multi-loaded transmission errors of Case 1，3 and 5

(1)二阶抛物线传动误差是四阶抛物线传动误差的一种特例(即系数a=0)，本质上就是小轮齿面沿接触迹线的四阶抛物线修形.

(2)仅改变滚比的多项式系数c1、c2和c3即可实现不同啮合转换点幅值的四阶传动误差设计，无需调整其他机床参数，易于磨齿加工实现.

(3)减小啮合转换点的四阶传动误差幅值，则在中、轻载条件下，承载传动误差波动较小;反之，则最小承载传动误差波动量所对应的载荷增大.

今后拟建立考虑四阶抛物线传动误差的动力学精确模型并进行齿轮副的振动和噪声验证.

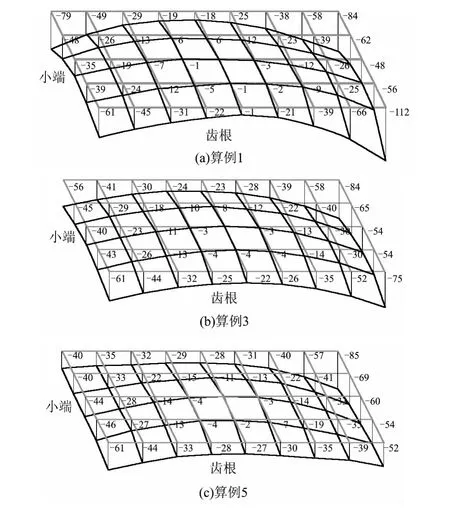
图7 算例1、3、5 的相对修形量Fig.7 Relative ease-off of Case 1，3 and 5

［1］Fong Z H，Tsay C B.Kinematical optimization of spiral bevel gears［J］.Journal of Mechanical Design，1992，114(3):498-506.

［2］方宗德，杨宏斌，周彦伟，等.高速弧齿锥齿轮动态啮合质量优化［J］.航空学报，2001，22(1):69-72.Fang Zong-de，Yang Hong-bin，Zhou Yan-wei，et al.Optimization of dynamic meshing behavior of high speed spiral bevel gears［J］.Acta Aeronautica et Astronautica Sinica，2001，22(1):69-72.

［3］方宗德，刘涛，邓效忠.基于传动误差设计的弧齿锥齿轮的啮合分析［J］.航空学报，2002，23(3):226-230.Fang Zong-de，Liu Tao，Deng Xiao-zhong.Tooth contact analysis of spiral bevel gears based on the design of transmission error ［J］.Acta Aeronautica et Astronautica Sinica，2002，23(3):226-230.

［4］Liu G L，Fan H W.Pinion tooth surface generation strategy of spiral bevel gears［J］.Chinese Journal of Mechanical Engineering，2012，25(4):753-759.

［5］Shih Y P.A novel ease-off flank modification methodology for spiral bevel and hypoid gears ［J］.Mechanism and Machine Theory，2010，45(5):1108-1124.

［6］Stadtfeld H J.The ultimate motion graph［J］.Journal ofMechanical Design，2000，122(3):317-322.

［7］Wang P Y，Fong Z H.Fourth-order kinematic synthesis for face-milling spiral bevel gears with modified radial motion(MRM)correction ［J］.Journal of Mechanical Design，2006，128(2):457-467.

［8］Wang P Y，Fan S C，Huang Z G.Spiral bevel gear dynamic contact and tooth impact analysis［J］.Journal of Mechanical Design，2011，133(8):084501/1-8.

［9］魏冰阳，方宗德，周彦伟，等.基于变性法的高阶传动误差设计与分析［J］.西北工业大学学报，2003，21(6):757-760.Wei Bing-yang，Fang Zong-de，Zhou Yan-wei，et al.On improving design of spiral bevel gear with high-order transmission error curve ［J］.Journal of Northwestern Polytechnical University，2003，21(6):757-760.

［10］Lee C K.Manufacturing process for a cylindrical crown gear drive with a controllable fourth order polynomial function of transmission errors［J］.Journal of Materials Processing Technology，2009，209(1):3-13.

［11］盛钢，沈云波.斜齿轮高阶传动误差设计与分析［J］.西安工业大学学报，2010，30(4):325-328.Sheng Gang，Shen Yun-bo.Design and analysis of helical gears with a high order transmission ［J］.Journal of Xi'an Technological University，2010，30(4):325-328.

［12］Su J Z，Fang Z D.Manufacturing process for circular-arc curvilinear cylindrical gears with predesigned fourth order transmission error［J］.Applied Mechanics and Materials，2011，37/38(10):623-627.

［13］方宗德.齿轮轮齿承载接触分析(LTCA)的模型和方法［J］.机械传动，1988，22(2):1-3.Fang Zong-de.Model and approach for loaded tooth contact analysis (LTCA)of gear drives ［J］.Mechanical Transmission，1998，22(2):1-3.

［14］Litvin F L.Local synthesis and tooth contact analysis of face-milled spiral bevel gears ［R］.Washington D C:Office of Management Scientific and Technical Information Division，National Aeronautics and Space Administration，1991.

［15］曹雪梅，方宗德，张金良，等.弧齿锥齿轮的齿面主动设计［J］.机械工程学报，2007，43(8):155-158.Cao Xue-mei，Fang Zong-de，Zhang Jin-liang，et al.Function-oriented active tooth surface design of spiral bevel gears［J］.Chinese Journal of Mechanical Engineering，2007，43(8):155-158.