机载LiDAR点云数据误差分析

2014-08-16熊爱武杨蒙蒙

测绘通报 2014年3期

熊爱武，杨蒙蒙

(1. 广州市欧科地理信息技术服务有限公司，广东广州 510663； 2. 北京四维远见信息技术有限公司，北京 100070)

一、引言

LiDAR系统是一种集激光扫描仪、全球导航卫星系统(GNSS)、惯性导航系统(INS) 和高分辨率数码相机于一体的主动式遥感系统。其中，激光扫描仪用于获取从激光发射(接收)参考点到探测目标的距离、扫描角和回波强度等数据，GNSS与INS组合导航可获得高精度的三维位置和姿态数据，高分辨率数码相机用于获取地物光谱、纹理信息。机载LiDAR系统具有高效快速、点云密度高、数据精度高、受天气影响程度小、成果产品丰富等优点，可快速获取数字表面模型(DSM)，生成高分辨率数字高程模型(DEM) 和高精度正射影像图(DOM)。它不仅在城市三维建模、地形测绘等领域有着广泛的发展前景，而且在电力行业、生态系统研究、环境监测等方面有着很大发展空间[1-3]。

由于LiDAR系统是一个多传感器集成系统，其各个传感器的误差影响会导致所得到的激光脚点坐标与真实值存在一定误差。目前已有不少学者对LiDAR系统误差进行了分析，有些学者着重分析机载激光扫描测距误差分析[3]，有些学者分析了误差对定位精度的影响[4]，还有些学者针对某几种误差进行分析[5]。系统误差分析和处理对于后续的数据处理和应用具有关键性的影响。

二、机载LiDAR系统工作原理

机载LiDAR系统是基于边角测量原理的主动式遥感系统，它利用激光测量激光发射(接收)参考点到被测目标点之间的距离和相应的指向角，利用POS(GNSS和IMU)获取测量平台的位置和姿态，通过距离、角度、位置、姿态数据计算被测目标点的坐标，具体数据模型为[1，3，6]

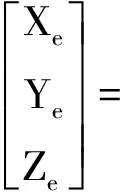
(1)

(2)

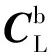
式(2)为在不同的基准间转换的数学模型，可以根据需要进行高斯投影或UTM投影计算。式中，下标r表示某一地心坐标系；T1、T2、T3表示两坐标系间的偏移量；D、R1、R2、R3表示由两个参考坐标系间三个定向参数组成的旋转矩阵的行列值。

三、机载LiDAR系统误差分析

根据上述模型，机载LiDAR系统的误差主要包括定位误差、GNSS/IMU组合系统误差、激光测距误差、激光测角误差、系统集成安置误差、时间同步误差、坐标转换误差、数据内插误差。

1. 定位误差

在机载LiDAR系统中，由于飞行平台与传感器的位置信息都是由GNSS数据确定的，因此影响机载LiDAR系统定位精度最主要的误差源于GNSS动态定位误差。机载LiDAR系统使用动态差分技术进行定位，而影响GNSS定位精度的主要误差源于GNSS卫星、卫星信号传播和地面接收设备。其中具体误差主要包括卫星星历误差、钟误差、相对论效应、多路径效应、天线相位中心变化、整周模糊度等。通过不同测站、不同历元、不同GNSS卫星的载波相位观测值进行差分，可以消除星钟误差、星历误差、接收机钟差和整周模糊度。用卡尔曼滤波估计周跳，采用GNSS伪距观测值与载波相位观测值进行组合解算，可以消除电离层的影响[4，7]。

2. GNSS/IMU组合姿态误差[7]

GNSS/IMU组合姿态误差主要是由陀螺仪和加速度计的误差引起的，主要包括惯性系统静态漂移误差、初始对准误差、动态跟踪误差等。静态漂移误差主要是由陀螺仪的漂移造成。在初始化对准的过程中，初始化对准结果所产生的导航坐标系偏离实际地理坐标系的差值即为初始化对准误差，初始化对准误差产生原因有两个：陀螺零偏和加速度计零偏。初始化对准精度取决于水平加速度计及东向陀螺，从数据处理角度看，初始化对准精度还取决于初始化对准时间。动态跟踪误差实际上就是INS误差的传播，在工作过程中，各种误差不断地积累而导致。

(1) GNSS/IMU系统漂移误差

陀螺本身所固有的随机误差为漂移误差

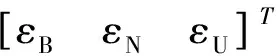
(3)

一般设定陀螺误差漂移模型为

ε=εb+εr+εg

(4)

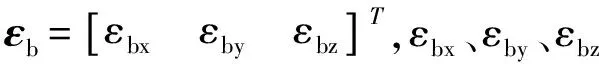
由于陀螺仪的漂移误差随着时间不断积累，可以采用多项式模型来拟合漂移误差，利用姿态角的近似计算可知INS获取姿态角误差模型为

(5)

式中，ψt为t时刻的姿态；ψ0为初始姿态角；a、b、c、d为模型参数值。

(2) 初始对准误差

INS通过积分惯性传感器测量值计算导航结果，导航方程每一次迭代，都是以上一次导航结果作为初始值进行的，因此在进行INS导航计算时，必须对它进行初始化，位置和速度的初始化需要外部设备提供，可以选用GNSS用户接收机。初始姿态信息可以通过外部信息提供，也可以由INS自身通过敏感重力矢量和地球自转矢量来确定。初始化过程称为对准，一般先对横滚角和俯仰角初始化，再进行方位的初始化，因为前者的精度影响方位对准的精度。

其中加速度计输出值的主要误差为

陀螺仪输出值的主要误差为

方位误差方程为

(6)

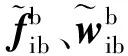
(3) 动态跟踪误差(INS误差传播)

引起INS产生位置、速度、姿态误差的原因来自：加速度计和陀螺仪的测量误差、导航方程近似和迭代频率受到限制而影响精度的误差、初始化误差。加速度计和陀螺仪零偏经过导航方程积分，在位置、速度、姿态方面的误差在不断地积累，导航计算误差也存在累积现象。姿态误差传递到速度误差，速度误差再次累积传递到位置误差，位置误差通过重力模型对导航产生积极、消极两方面的影响，因此完全确定INS误差传播中的误差是一个非常复杂的问题，需要深入系统内部，对每一个环节都要控制精度。

3. 激光测距误差

激光扫描仪的测距精度是机载LiDAR标定的重要指标之一。影响测距的误差因子较多，测距模型可以表示为

L=L′+ξ1+ξ2+ξ3+ξ4

(7)

式中，L为距离改正值；L′为距离量测值；ξ1误差是指激光扫描仪自身误差；ξ2误差是指大气折射误差；ξ3误差指大气扰动与激光束漂移误差；ξ4误差指回波强度对距离造成的影响。

(1)ξ1误差

ξ1误差模型为

ξ1=ΔR1+ΔR2+ΔR3+(K1L′+K2)

(8)

ξ1包括仪器本身常数修正、时间延迟误差ΔR1、光电转换及后置电路延迟误差ΔR2、时间间隔误差ΔR3。其大小与系统自身的性能、地形条件等外界条件有关。其中激光扫描仪自身的仪器常数,利用加常数K2和乘常数K1来对原始测定值进行修正，加常数是由于仪器电子中心与机械中心的不重合造成的，乘常数是由于测距频率偏移而产生的。

(2)ξ2误差

激光雷达的性能是与激光在大气中的折射效应密切相关的，要充分发挥激光雷达的特性，就要修正大气折射效应对激光脚点造成的定位误差。大气折射率为

n=1+N(λ,T,P,e)

(9)

式中，λ为激光波长；T为空气温度；P为大气压强；e为湿度；N为大气折射率模数，量级为10-6，在标准大气下，可见光-红外波段激光的大气折射率为

N0(λ)=272.579 4+1.583 2λ-2+0.015λ-4

(10)

由此，在任意情况下

N(λ)=N0(λ)(2.843 4×10-3P/T-0.112 7e/T)

(11)

由上述计算公式，精度可达10-8～10-7，N的计算通常写为N=0.79P/T。

(3)ξ3误差

ξ3误差指大气扰动与激光束漂移误差，其中大气扰动的折射率变化可以用结构函数来表示为

Dn(ρ)=<[n(r2)-n(r1)]2>

(12)

式中，r1、r2表示空间位置；n(r1)、n(r2)分别为相应位置的空气折射率;ρ=r2-r1，代表距离；〈〉代表时间平均。从理论和实践中得出，折射率的随机变化和距离的1.5次方成比例，即

(13)

式中，Cn称做l0到L0区间的结构参数，是折射率起伏变化的描述，它和大气参数(如热流、风速、高度)有关；l0为最小非均匀旋涡的尺寸，典型值为1～10 mm；L0为最大非均匀尺度，它和离地面的高度有关，近地表面处的干扰要大一些。消除这些误差，可以采用机械和光学方法。

激光束漂移误差：激光扫描仪都采用激光束的能量中心作为测量基准，采用复合棱镜组可实现对光束能量中心漂移的补偿。

(4)ξ4误差

ξ4误差指回波强度对距离造成的影响(不同地物对测距造成的误差)。不同地物对测距造成的误差，反映在回波强度对距离造成的影响上，将激光扫描仪的回波强度范围设置为0～2047，尽可能多地细分等级，回波强度与目标地物的灰度值有一定的关系，一般灰度值越高，回波强度越大。通过多次试验，统计出回波强度对距离改正表，见表1。

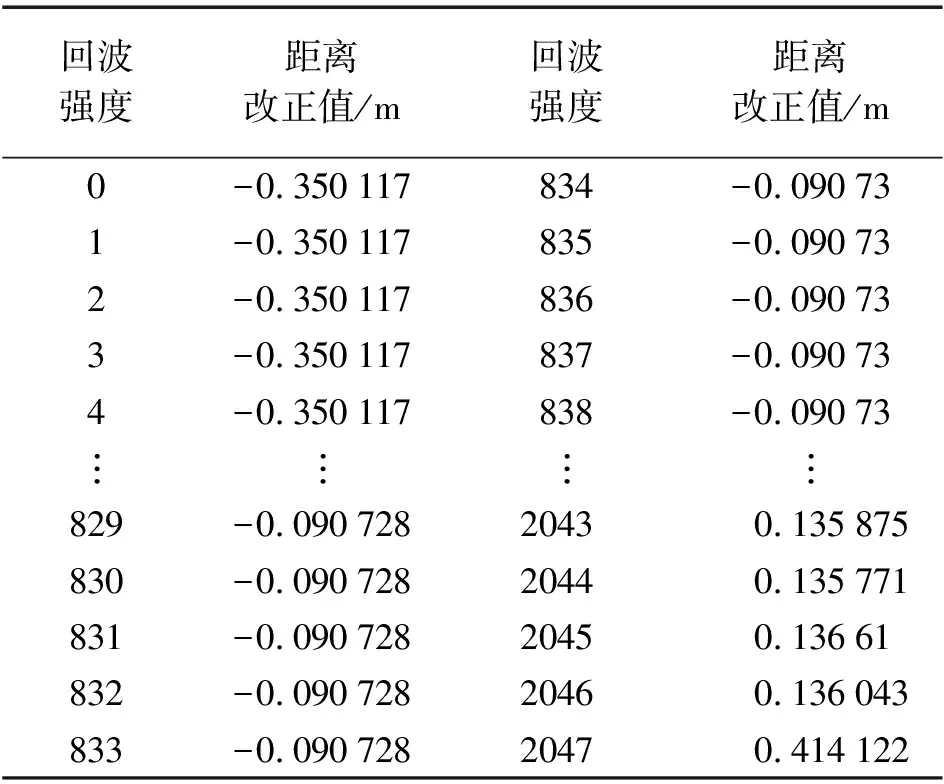
表1 回波强度对距离的改正

4. 激光测角误差

机载LiDAR集成系统在进行作业的过程中，由于存在各种原因，会导致扫描角量算时存在测量误差。对于旋转扫描镜，通常假定激光扫描仪内部的扫描镜是匀速转动，在以扫描行为单位的周期里，每个采样点对应的扫描角是根据扫描视场角范围之内与每行采样点数计算的。但实际上，由于设备在制造的过程中不可能实现扫描镜绝对的匀速转动，因此以匀速转动为前提计算的扫描角与实际情况存在一定的偏差。

扫描角误差Δβ是在激光扫描仪工作过程中随着扫描角β的变大而增加的，它实际上是绕X轴偏转的一个比较小的角度，并且安装时，激光扫描平面不可能绝对垂直于激光参考坐标系的X轴。这就使得实际的激光扫描平面绕激光参考坐标系各有一个小的旋转角度Δφ、Δω。

扫描角误差对定位的误差模型由下列公式表达

(14)

式中，ΔXL、ΔYL、ΔZL代表激光坐标系下引起的偏移量；l为经过测距误差改正后的值;a、b为激光扫描镜内的固定参数；fx、fy、fz分别代表在激光坐标系X、Y、Z三方向定位函数；ΔRφ、ΔRω代表角度Δφ、Δω旋转的误差矩阵。

5. 系统集成安置误差

(1) 偏心距误差

偏心距误差主要是指IMU中心到GNSS天线相位中心的距离及激光扫描仪中激光束发射点到IMU系统中心之间的距离的安置误差。在系统集成之后，需要量测各传感器之间的相对位置关系，而观测存在误差，导致偏心距误差的产生。因此这两偏心距必须测量准确。

(2) 视轴误差

视轴误差是指激光扫描坐标系与IMU坐标系之间的不平行导致的误差，包括横滚角误差、俯仰角误差和航向角误差，这些误差随着时间逐渐发生变化，尤其在航带重叠处可明显看到，需要对采集数据进行检校。定义飞行方向为Xb轴，旁向为Yb轴，高程方向为Zb轴，横滚角误差是逆着Xb轴逆时针选择为正，随着扫描角的增大，对测距造成的误差变大；俯仰角误差指逆着Yb轴逆时针旋转为正；航向角误差指逆着Zb轴逆时针旋转为正，会造成测距不准确，主要会使航线轨迹发生扭曲。视轴误差可以通过飞行特殊地物的检校场，从点云数据中提取相应数据进行迭代运算，获得横滚角误差、俯仰角误差和航向角误差，然后将其代入坐标计算数据模型中，计算点云的精确坐标。

6. 时间同步误差

机载LiDAR系统各传感器之间是独立的，具有不同的时间记录器。要获取目标地物精确的三维信息，定位、定向、测距都必须保持在同一时刻进行。如果存在时间偏差，将会造成定位影响，并且这种影响造成的误差是不断发生变化的，并不是一个恒定的常量。为了获取同一时刻的激光脚点的姿态、距离、位置信息，需统一各传感器的时间系统到UTC时间系统中。该系统涉及3种时间同步：GNSS与IMU的时间同步、LiDAR与POS(GNSS/IMU)的时间同步、LiDAR与数字相机的时间同步。目前GNSS与IMU的时间同步主要是通过GNSS接收机提供1PPS(pluse-per-second)实现的；LiDAR与高精度POS的时间同步主要是通过激光扫描仪发送PPS脉冲信号给GNSS来实现的；LiDAR与数字相机之间的时间同步主要是依靠LiDAR控制系统发送脉冲给数字相机使相机曝光，从而实现GNSS、IMU、LiDAR、数字相机四者之间的时间同步。

7. 坐标转换误差

在坐标转换的过程中，选择不同坐标系之间的转换，得到WGS-84坐标，而在一般工程应用中，需要将坐标转换到平面坐标系下，这些工程中都存在着坐标转换误差。因此，可以根据工程需要，选择相应精度的转换模型和转换参数。

8. 数据内插误差

由于机载LiDAR集成系统内，各传感器的采样频率不同，将造成数据处理过程中的数据内插误差。一般激光扫描仪的频率最高，可达到200 kHz，IMU最高采样频率为200 Hz，GNSS采样频率为1 Hz，相机可以根据需求设置频率，来实现定点定时曝光。因此要想得到每个激光采样点的位置和姿态，需要对GNSS与IMU数据进行内插处理，在进行航空摄影过程中，POS观测历元时刻ti与IMU的采样时刻tj往往不能同步，一般认为飞机在航空摄影工作的过程中是匀速进行的，POS系统采用线性内插的方法进行，但实际上，飞机飞行速度很难保持匀速进行，同时对于每一个激光采样点要获取其位置和姿态，必须通过内插处理来获取，将不可避免地存在数据内插误差。