高超声速飞行器姿态角速度的全通道鲁棒镇定方法

刘晓东 黄万伟 柳嘉润 孙 勇

1. 北京航天自动控制研究所, 北京 100854 2. 宇航智能控制技术国防科技重点实验室, 北京 100854



高超声速飞行器姿态角速度的全通道鲁棒镇定方法

刘晓东1,2黄万伟1,2柳嘉润1,2孙 勇1

1. 北京航天自动控制研究所, 北京 100854 2. 宇航智能控制技术国防科技重点实验室, 北京 100854

根据高超声速飞行器的姿态动力学方程，给出一个可面向姿态角速度镇定的非线性设计模型。针对一类非线性系统，提出一种基于扩张状态观测器(ESO)的鲁棒动态逆设计方法，并将其应用于高超声速飞行器姿态角速度的渐近镇定中。仿真结果表明，相比传统的动态逆控制方案，本文所提出的控制方案可保证飞行器姿态角速度得到快速镇定，并且具备针对模型不确定和结构干扰力矩的强鲁棒性能。

高超声速飞行器；角速度镇定； 动态逆控制； 鲁棒控制； 扩张状态观测器

与一般的飞行器相比，高超声速飞行器3通道之间面临着更为复杂的非线性动态、高不确定性和强耦合等问题，传统的线性控制方法很难满足其姿态角速度快速镇定的需求，最终导致飞行任务的失败。为了解决上述问题，有必要从全通道、非线性设计的角度出发，探索具有强鲁棒性能的姿态角速度镇定技术[1]，而本文正是基于此展开的。

动态逆控制(Dynamic Inversion Control，DIC)[2-3]技术通过选择非线性反馈函数将非线性系统线性化，实现由不理想动态向理想动态的转变。在面对多输入多输出非线性系统的控制问题时，动态逆方法可以大大简化设计过程。但是，传统的动态逆控制要求模型动态过程被完全模型化，并且可被精确抵消，这在实际应用中是不现实的。因此，需要采取某种形式的鲁棒控制策略来抑制由于模型不确定性带来的性能偏差。本文将从不确定动态估计与补偿的角度出发，通过设计某种形式的干扰观测器，降低不确定性对动态逆控制系统的影响。

自抗扰控制技术(Active Disturbance Rejection Control，ADRC)[4]是一种可以实时估计并补偿系统不确定动态的鲁棒控制技术，该控制技术不需要精确的模型信息，也不需要假设不确定模型为参数线性化或有界，故其通用性较高。在高超声速飞行器控制领域，自抗扰控制已得到了广泛的研究[5-7]，并展示出传统控制方法无可比拟的效果。实际上，自抗扰控制的强鲁棒性能主要得利于扩张状态观测器(Extended State Observer，ESO)的引入，ESO可以较为精准地估计出系统当前的未知不确定性，其输出将被补偿到控制系统中，而补偿之后的控制系统结构较为简单，易于进一步的设计和分析。综合考虑估计精准性、控制量平滑性以及算法的复杂程度，本文将引入一种线性ESO，以克服传统动态逆控制的鲁棒性能缺陷。基于ESO的动态逆控制将用于高超声速飞行器姿态角的渐近镇定中。

1 问题描述

考虑关于纵向平面对称的高超声速飞行器对象，以力矩作为输入，其姿态动力学模型可以描述为[8]：

(1)

式中，ωx1，ωy1，ωz1为机体轴角速度，Jx1，Jy1，Jz1为飞行器的主转动惯量，Jx1y1表示惯性积，Mx1，My1和Mz1分别为滚转力矩、偏航力矩和俯仰力矩。由式(1)可以看出，飞行器滚转、偏航和俯仰3通道之间存在惯性耦合和运动耦合，这些耦合因素会影响姿态角速度的渐近镇定过程，因此需要在控制律的设计过程中予以充分考虑。

(2)

式中：

因为Jx1Jy1-Jx1y1≠0，故控制矩阵g(x)是可逆的。显然，若直接针对模型(2)进行姿态角速度的镇定方案设计，将会大大增加设计的难度。

因为惯性积Jx1y1较小且不易被精确测量，故可以将其相关项视为系统不确定动态。同时，在设计过程中，将使用主转动惯量的名义值(即测量值)Jnx1，Jny1和Jnz1。这样，可面向姿态角速度镇定方案设计的数学模型如下：

(3)

式中：

此外，向量ξ表示建模误差和干扰力矩等不确定动态。

于是，模型(3)为姿态角速度镇定方案的构造提供了设计依据，而原模型(1)为后期的仿真验证提供了实际对象的构建依据。

2 飞行器姿态角速度镇定方案设计

2.1 基于ESO的动态逆设计

对于如下的n维非线性系统：

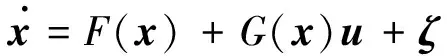
(4)

式中：G(x)是非奇异的且可以近似获得。假设系统的一部分内部动态是可知的，则式(4)可以改写为如下的形式：

(5)

式中：F0(x)表示已知的内部动态，而Fn(x)表示未知动态。那么，需要扩展的状态向量为：

(6)

针对式(5)～(6)，可以设计如下的线性ESO，用于系统不确定动态的估计：

(7)

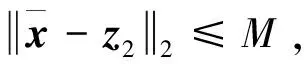
u=-G-1(x)[F0(x)+Wx+z2]

(8)

证明：选取Lyapunov函数如下：

(9)

等式2边分别对时间进行微分，可得：

(10)

式中：W=2W1，故W1为正定矩阵。

根据文献[9]中的数学证明过程，可得如下不等式：

(11)

(12)

根据向量2-范数的定义[10]可得：

(13)

式中：xi表示向量x的第i个状态变量。

2.2 姿态角速度鲁棒镇定方法设计

基于可面向姿态角速度镇定的设计模型(3)，并利用定理1中的结论，可设计如下的姿态角速度控制律：

(14)

其中，线性ESO可以设计为如下的形式：

(15)

至此，关于高超声速飞行器姿态角速度的全通道鲁棒镇定方案设计完毕。下面将通过计算机仿真手段，验证该方案的有效性和合理性。

3 仿真结果

本节将对比本文镇定方案与传统动态逆镇定方案的仿真结果，并分析本文方案的优势。

仿真中，高超声速飞行器主转动惯量的名义值为：

Jnx1=150kg·m2,Jny1=3000kg·m2,
Jnz1=2800kg·m2。

为了更清楚的对比2种控制方案，对于实际的转动惯量，考虑10%的误差。实际的惯量积取为Jx1y1=-10kg·m2，为控制中的未知项，加入了3通道的等效干扰如下：

ξ1=2.0+1.0sin(4πt),ξ2=1.0+0.2sin(4πt),

ξ3=1.2+0.2sin(4πt)。

除此之外，考虑到实际工程情况，滚转力矩、偏航力矩和俯仰力矩的限制幅值分别为1500N·m，10000 N·m和12000 N·m。

鲁棒动态逆控制律的参数值如下：W=diag[100, 100, 100],β0=1000,β1=250000。

在初始时刻，假设滚转角速度、偏航角速度和俯仰角速度分别为10(°)/s,5(°)/s和5(°)/s。下面将比较2种控制方案下高超声速飞行器姿态角速度的镇定情况，如图1所示。

图1 2种控制方案下姿态角速度曲线

通过图1可以看出，相比传统动态逆控制方案，基于ESO的动态逆控制方案对高超声速飞行器姿态角速度的镇定作用更强。而且，由于时变等效干扰的加入，2种控制方案下姿态角速度存在不同幅度的等频波动。但相比之下，本文控制方案的波动幅度要小得多，这就充分说明了该方案具备更强的鲁棒性，体现了其性能优势。

此外，下面将给出本文控制方案下的控制力矩曲线，如图2所示。可以看出，各控制力矩的波动频率与所加入等效干扰的一致，体现了本文方案针对等效干扰的调节作用。而且，控制量曲线较为平滑，因此提高了本文方案的工程实用价值。

图2 控制力矩曲线

4 结论

针对高超声速飞行器3通道间复杂非线性、高不确定性和强耦合的特点，从全通道、非线性设计角度出发，提出了基于ESO的动态逆镇定方案，可保证飞行器姿态角速度快速渐近收敛，并且具备针对建模误差、未建模动态以及结构干扰力矩的强鲁棒性能。仿真结果表明，相比基于传统动态逆的镇定方案，本文鲁棒镇定方案下飞行器姿态角速度的收敛性能更好，稳定性更高。此外，本文控制方案结构较为简单，易于工程实现。

[1] 张兵, 吴洪鑫.二维完整配置下刚性航天器姿态角速度的渐近镇定[J]. 自动化学报, 2000, 26(4): 547- 551. (Zhang Bing, Wu Hongxin. Asymptotical Stabilization of Angular Velocity of A Rigid Spacecraft with Two- Dimensional Complete Configuration[J]. Acta Automatica Sinica, 2000, 26(4): 547- 551.)

[2] Slotine J and Li W. Applied Nonlinear Control [M]. 3rd ed., NJ: Prentice- Hall, 1991.

[3] Sonneveldt L, Chu Q P, and Mulder J A. Nonlinear Flight Control Design Using Constrained Adaptive Back-stepping[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(2): 322- 336.

[4] 韩京清. 自抗扰控制技术—估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2007.(Han Jingqing.Active Disturbance Rejection Control Technique- The Technique for Estimating and Compensating The Uncertainties[M]. Beijing: National Defense Industry Press, 2007.)

[5] 秦昌茂, 齐乃明, 朱凯.高超声速飞行器自抗扰姿态控制器设计[J].系统工程与电子技术, 2011, 33(7): 1607- 1610.(Qin Changmao, Qi Naiming, Zhu Kai. Active Disturbance Rejection Attitude Control Design for Hypersonic Vehicle[J]. Systems Engineering and Electronics, 2011, 33(7): 1607- 1610.)

[6] 齐乃明, 秦昌茂, 宋志国.高超声速飞行器改进自抗扰串级解耦控制器设计[J].哈尔滨工业大学学报, 2011, 43(11): 33- 38.(Qi Naiming, Qin Changmao, Song Zhiguo. Improved ADRC Cascade Decoupling Controller Design of Hypersonic Vehicle[J].Journal of Harbin Institute of Technology, 2011, 43(11): 33- 38.)

[7] 栗金平, 杨军．基于自抗扰技术的高超声速飞行器控制系统设计[J].计算机测量与控制, 2011, 19(5): 1055- 1057, 1064.(Li Jinping, Yang Jun. Design of Hypersonic Vehicle Control System Based on Auto Disturbance Rejection Control[J].Computer Measurement and Control, 2011, 19(5): 1055- 1057, 1064.)

[8] 钱杏芳, 林瑞雄, 赵亚男.导弹飞行力学[M].北京: 北京理工大学出版社, 2000.(Qian Xingfang, Lin Ruixiong, Zhao Yanan.Missile Flight Mechanics[M]. Beijing: Beijing Institute of Technology Press, 2000.)

[9] 刘晓东, 吴云洁.一种变结构控制系统设计方法[J].电机与控制学报, 2013, 17(6): 75- 81.(Liu Xiaodong,Wu Yunjie.Design Method of Variable Structure Control System[J].Electric Machines and Control, 2013, 17(6): 75- 81.)

[10] Mitrinovic D S, Pecaric J E, and Fink A M. Classical and New Inequalities in Analysis[M]. Kluwer Academic, 1993: 83- 134.

All-ChannelRobustStabilizationMethodforAttitudeAngularSpeedofHypersonicVehicle

LIU Xiaodong1,2HUANG Wanwei1,2LIU Jiarun1,2SUN Yong1
1. Beijing Aerospace Automatic Control Institute, Beijing 100854, China 2. National Key Laboratory of Science and Technology on Aerospace Intelligence Control, Beijing 100854, China

Accordingtotheattitudedynamicsequationsofhypersonicvehicle,anonlinearmodelorientedtoattitudeangularspeedstabilizationisestablished.Regardingaclassofnonlinearsystem,arobustdynamicinversioncontrol(DIC)approachisproposed,whichisbasedonextendedstateobserver(ESO),andthenitisutilizedtostabilizetheattitudeangularspeedofhypersonicvehicle.Thesimulationresultsshowthat,theproposedcontrolschemecanensuretheattitudeangularspeedofchosenvehicleisstabilizedmorerapidlybycomparingwiththetraditionalDICschemeanditpossessesmorerobustpropertywithrespecttomodelinguncertaintiesandstructuraldisturbancetorques.

Hypersonicvehicle；Angularspeedstabilization；Dynamicinversioncontrol；Robustcontrol；Extendedstateobserver(ESO)

2014- 05- 13

刘晓东(1987-)，男，山东人，在站博士后，主要研究方向为飞行器制导与控制技术、伺服系统控制技术等；黄万伟(1970-)，男，湖南人，博士，研究员，主要研究方向为飞行器先进控制理论与应用、导航与制导技术等；柳嘉润(1979-)，男，湖南人，博士，高级工程师，主要研究方向为飞机综合控制、自主空战决策和运载火箭姿态控制等；孙勇(1984-)，男，山东人，博士，工程师，主要研究方向为飞行控制和优化计算等。

TJ765.2

： A

1006- 3242(2014)06- 0003- 05