有限单元法库区渗流场数值模拟及敏感性分析
2014-08-10王健平蔡昌渊
王健平 蔡昌渊 刘 晖
(国网新源富春江水力发电厂,浙江 桐庐 311500)
·水利工程·
有限单元法库区渗流场数值模拟及敏感性分析
王健平 蔡昌渊 刘 晖
(国网新源富春江水力发电厂,浙江 桐庐 311500)
采用FORTRAN程序,编写了调用针对东部某抽水电站上库区渗流场数值模拟的计算程序,研究了库区渗流场的计算方法,并论证了该计算方法的正确性和实用性,分析结果证明该计算方法适应性强、精度高、应用方便、实用性好。
水文地质,有限单元法,渗流场,数值模拟,敏感性分析
库区地下水渗流分析多以线性的达西定律为基础,这是因为在大多数情况下,地下水渗流是满足或近似满足达西定律的,而且达西定律所表达的线性关系也使理论分析与数值分析较为简洁,然而修建在岩溶地区的大坝基础中可能存在强透水地质构造,渗流的雷诺系数很大,渗流速度与水力坡度不再遵从达西定律,此时必须考虑惯性力的影响。柴军瑞(2001年)[1]、代群力(2000年)[2]认为有必要对岩溶区进行坝基地下水非线性渗流分析。由于非线性渗流的复杂性,至今仍没有一个统一的公式来更好地描述这种流动,其中两个常用的经验公式模型为Forchheimer公式[3],将其代入一般情况下三维空间渗流的连续性方程,即可得到非线性渗流公式。有限单元法是一种较为常用的数值方法。它是古典变分法与分块多项式插值结合的产物,它的核心是对区域的离散化。1965年,津克维茨(Zienkiewiz)和张(Cheung)提出有限单元法适用于所有可按变分形式进行计算的场问题,为该方法在渗流分析中的应用提供了理论基础。Leiws R W等(1987年)[4]将这一方法用于模拟多孔介质中的地下水。国内不少研究[5,6]认为有限单元法是一种先进有效的数值模拟法,用于渗流分析计算时可部分替代模型试验,精度相对较高,可方便地模拟多种外部条件的特点。本文采用自己编写的FORTRAN程序,调用了针对该具体工程条件编写了有限元计算程序,并进行了参数反演分析,计算结果较为理想。
1 工程实例
东部某抽水蓄能电站装机容量1 350 MW。电站枢纽由上水库(见图1)、下水库、输水系统、地下厂房等建筑物组成。上水库面板堆石坝最大坝高183.5 m,总库容1 703万m3;下水库面板堆石坝最大坝高33.4 m,总库容1 676万m3。工程区北邻长江,南望太湖,属宁镇山脉的低山丘陵区,地势总体是西高东低,地形切割不深,沟谷稍发育,以冲积堆积、剥蚀地貌为主,区内普遍可见数级剥夷面和3级~4级阶地,以及相应的成层岩溶、深切河谷。

工程区从岩溶发育程度、地层岩性、地质构造及岩溶水赋存运移特征来划为四类岩溶水文地质单元(区),一类非可溶岩分布区;其中:A区——裸露型纯碳酸盐岩单斜岩溶发育强度弱~中等水文地质单元(区),地表基岩大片裸露,岩性由白云岩类逐渐变为灰岩类;西侧以F7断层为界,北侧以F4断层为界,东侧为仑山东面坡脚下水库库区F12-1断层及其伴生的闪长玢岩脉和龙潭组(P2l),南侧以仑山南面坡脚奥陶系上统(O3)为界,位于工程区上水库、输水发电系统枢纽工程部位,为本文渗流场分析区;B区——覆盖型纯碳酸盐岩与非可溶岩互层(或夹层)岩溶发育强度中等水文地质单元,分布在仑山坡脚,下水库西侧库岸;C区——裸露型背斜岩溶发育强度弱~中等水文地质单元,位于上水库的西侧;非可溶岩由粉砂岩、粗面岩、闪长玢岩等组成,主要分布在下水库的北侧及仑山的南侧坡脚仑山水库一带。
2 渗流场数值模拟及结果分析
2.1 数学模型的建立
由于枯水期地下水变化不大,因此可以将地下水运动概化为稳定流。该计算区域内的地下水运动可以概化为在一个非均质各向同性介质中的二维流动,其数学模型如下:
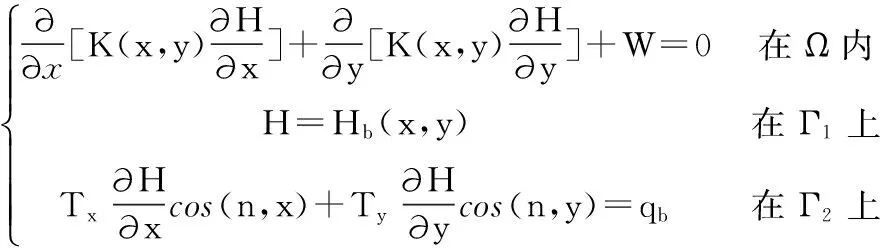
其中,Ω为计算区域;Γ1为第一类边界;Γ2为第二类边界;Hb为第一类边界上的已知水头;n为第二类边界上的外法线方向;qb为第二类边界上法向的单宽流量,流入为正,流出为负;W为降雨入渗补给量。将其简写为有限元方程式,即为:
[G]{H}={W}+{F}。
由此得到一个NN阶线性方程组,解方程组就可得出NN个节点的水头。
2.2 几何模型的建立及参数的选取
根据地层岩性、岩溶水文地质单元,结合地形地貌特征,将研究区分为5个区(如图2所示)。北部边界沿着F3断层,南部边界至F9断层,东部以姊妹桥F12断层附近钻孔25所在一线为边界,西部以F7为边界。
Ⅰ区:F4断层与F3断层之间的志留系坟头组的砂岩、粉砂岩;Ⅱ区:F7断层与F8断层之间北至断层F4,南至仑山山脊;Ⅲ区:由断层F12与断层F8与仑山山脊围成的三角形区域;Ⅳ区:F7断层与F8断层之间,仑山山脊以南的部分;Ⅴ区:F8断层以东,仑山山脊以南部分。将研究区域剖分为2 056个三角形单元,1 092个节点,见图3。

为了充分利用观测资料,将上库区的钻孔地下水水位作为上库第一类边界条件;下库区泉水出露的点作为流量边界。
参数选取采用钻孔压水试验换算值和经验值相结合的方法。根据钻孔压水试验资料,渗透Ⅰ区渗透系数值取0.017 5 m/d;渗透Ⅱ区渗透系数取0.008 64 m/d;渗透Ⅲ区渗透系数值取0.019 5 m/d;渗透 Ⅳ区渗透系数值取0.021 m/d;渗透Ⅴ区渗透系数值取0.018 7 m/d。考虑库盆中降雨入渗补给,根据仑山水库降雨量资料,一月份平均降雨量为46.1 mm,即1.54 mm/d。在库盆中地表水绝大部分渗入地下,因此降雨入渗补给系数取0.55。
2.3 数值模拟结果及分析
根据上述数学模型,采用FORTRAN编写的二维有限元程序进行了模拟计算,库区渗流场等水位线如图4所示。
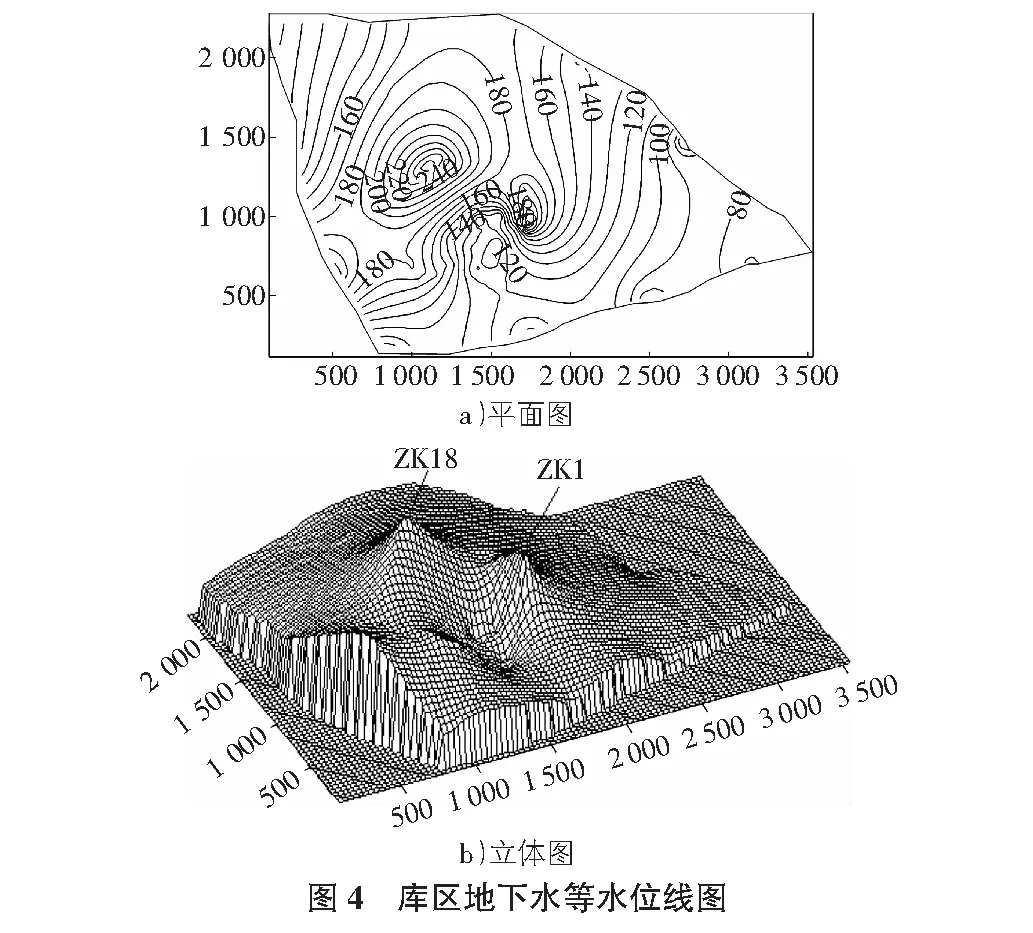
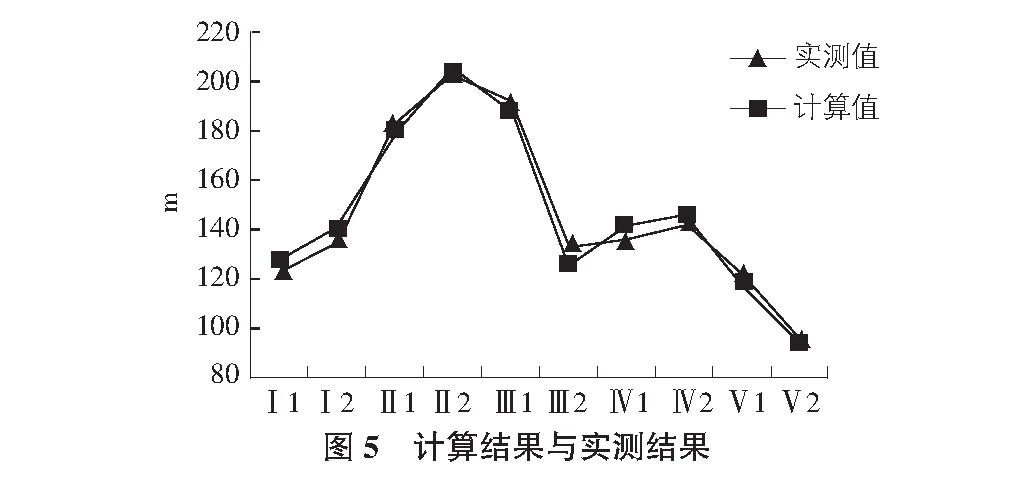
在上库的主体部分,其西北、西及西南三侧分水岭均位于本亚区。从地下水等水位线图中可以看出,地下水分水岭与地表水分水岭基本一致。地下水总体上由上库向四周补给,由于南北两侧的非可溶岩(微透水层)的阻水作用,地下水在南侧和北侧以泉的形式排泄。仑山山脊一带存在一个分水岭,地下水在总体上向东流的同时,还向分水岭的南、北两侧流动。在上库南侧,地下水向大哨泉以北的冲沟中排泄;东侧地下水向正东排泄至姊妹桥方向;在北侧,存在一近南北向的分水岭,地下水向北流动的同时分别向东、西两侧排;在西侧,地下水向钥匙湾流动,这与地表水的流向基本一致。为了更好的表明计算的精度,分别在5个区各设立了2个地下水水位观测点,共计10个地下水水位观测点,现将计算值与实测值进行对比。计算结果与实测结果见表1及图5。

表1 计算结果与实测结果
由表1及图5不难看出,计算结果与实际测量值较为接近,其中最大误差未超过5 m,分别出现在Ⅰ2和Ⅲ1处;而最小误差为2 m,出现在Ⅴ2监测点,最大相对误差为2.6%,可见模型具有一定的精度,同时证明该方法具有一定的正确性和实用性。
3 模型参数敏感性分析
由于研究区地质及水文地质研究处于进一步研究阶段,许多参数还不确定,因此可以通过参数敏感性分析来研究不同参数时的地下水运动状态,分析参数对渗流场的敏感性。
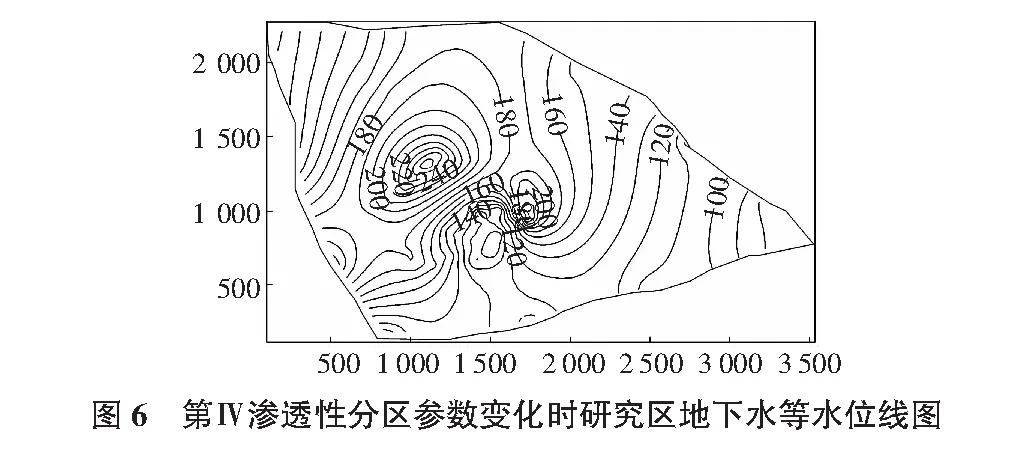
第Ⅳ渗透性分区中,岩溶发育较强,其渗透系数增加1倍,其余参数不变。计算结果如图6所示。
第Ⅰ渗透性分区中,岩溶发育较弱,其渗透系数减小1/2倍,其余参数不变。结果见图7。
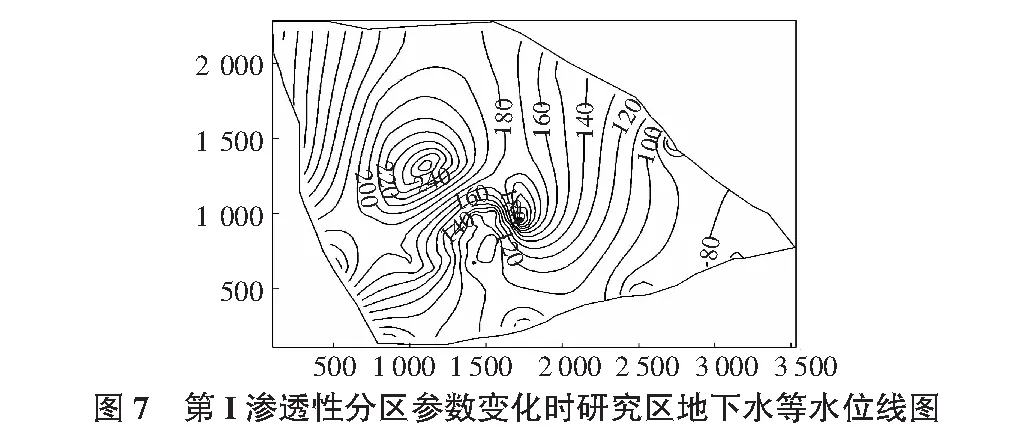
第Ⅲ渗透性分区中,岩溶发育相对较弱,为了从保守的角度考虑,其渗透系数取值与第Ⅳ渗透性分区一致,其余参数不变。计算结果如图8所示。
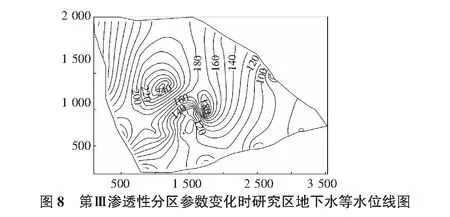
从图6~图8中可以看出,第Ⅳ渗透性分区渗透参数的变化对地下水渗流场变化有较大的影响,但总的趋势与图4一致。其他区域渗透参数变化时,地下水渗流场变化不明显,即地下水渗流场对其他区域渗透参数变化不敏感。
通过对研究区渗流场进行计算分析可知,ZK1钻孔以东仑山南北坡之间仍存在一分水岭,地下水在向分水岭南、北两侧流动的同时,总体上还向东流动。仑山南北坡由于非可溶岩的阻水作用,地下水在南侧和北侧以泉的形式排泄。本次计算中没有单独划分这一高渗透性区域,因而计算结构没有反映低水位槽的情况,渗流计算仅给出了研究区地下水运动的总体趋势。
F8断层以东的区域渗透性参数变化对地下水渗流场有较大的影响,其余区域渗透参数变化对地下水渗流场不敏感。
4 结语
1)根据实际工程应用的需要,采用FORTRAN程序,调用编写的计算程序能够真实模拟库区渗流场情况,证明该方法具有一定的正确性和实用性。2)从地下水等水位线图中可以看出,地下水分水岭与地表水分水岭基本一致。地下水总体上由上库向四周补给,由于南北两侧非可溶岩的阻水作用,地下水在南侧和北侧以泉的形式排泄;东侧地下水向正东排泄至姊妹桥方向;在西侧,地下水向钥匙湾流动。3)通过参数反演可知,第Ⅳ渗透性分区渗透参数的变化对地下水渗流场变化有较大的影响,其他区域渗透参数变化时对地下水渗流场影响不大。
[1] 柴军瑞.坝基非达西渗流分析[J].水电能源科学,2001,19(4):1-3.
[2] 代群力.地下水非线性流动模拟[J].水文地质工程地质,2000(2):50-51.
[3] BEAR J.HYDRAULICS OF GROUND WATER[M].NEW YORK:MCGRAW-HILL,1979.
[4] LEIWS R W,SCHREFLER B A.THE FINITE ELEMENT METHOD IN THE DEFORMATION AND CONSOLIDATION OF POROUS MEDIA[M].NEW YORK:JOHN WILEY,1987.
[5] 李康宏,柴军瑞.坝基渗流分析两种数值方法的比较[J].红水河,2003,22(4):14-17.
[6] 闫澍旺,王瑞钢,王学军,等.白石水库渗流场有限元分析[J].水力发电学报,2003(2):53-61.
Numerical simulation of reservoir seepage field the finite element method and the parameter sensitivity analysis
WANG Jian-ping CAI Chang-yuan LIU Hui
(StateGridXinyuanFuchunjiangHydropowerPlant,Tonglu311500,China)
The paper adopts FORTRAN procedure, compiles the calculation program of the numerical simulation for some hydropower station reservoir in the east part of China, researches the calculation methods of the seepage field of the reservoir, indicates its accuracy and application, proves by the analysis result that the method is adoptable and practical with high accuracy and convenient application.
hydrogeology, finite element method, seepage field, numerical simulation, sensitivity analysis
1009-6825(2014)30-0232-03
2014-08-12
王健平(1964- ),男,高级工程师; 蔡昌渊(1978- ),男,工程师; 刘 晖(1987- ),男,助理工程师
TV139.1
A
