有界线性算子的Drazin逆的扰动

武淑霞

(四川民族学院数学系，四川康定626001)

有界线性算子的Drazin逆的扰动

武淑霞

(四川民族学院数学系，四川康定626001)

给出了Drazin可逆算子在一个扰动下仍Drazin可逆的充分条件及Drazin逆的表达式，并根据给出的表达式，探讨了相关的误差估计界．

Drazin逆；算子矩阵；扰动；范数

设H是一个无限维Hilbert空间，B(H)表示H中所有有界线性算子的全体．对于算子A∈B(H)，R(A)、N(A)、σ(A)分别表示A的值域、核空间与谱．

对于算子A∈B(H)，若存在AD∈B(H)满足以下三个方程

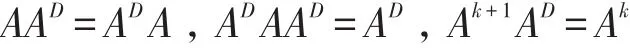
则称AD为算子A的Drazin逆，其中k=ind(A)称为A的指标．对于算子A∈B(H)，若其Drazin逆存在，则A的Drazin逆AD是唯一的．

设S为B(H)上的可逆算子，若A∈B(H)Drazin可逆，则S-1AS仍Drazin可逆且(S-1AS)D=S-1ADS．

设算子A∈B(H)Drazin可逆且ind(A)=k，则在空间分解H=R(Ak)⊕R(Ak)⊥下，存在可逆算子P，使得

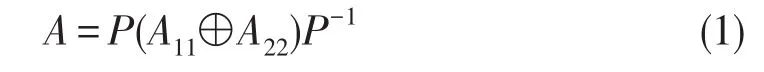
其中A1为可逆算子，A2是指标为k的幂零算子，且有

将A的扰动算子E∈B(H)按照(1)分块为

杨凯凡等[1]给出了算子A在E的扰动下，其扰动算子的Drazin可逆性与表达式，但在计算的过程中没有考虑到指标的变动，因此结果没有化简完全．本文讨论了算子A的扰动的Drazin可逆性，并给出了指标化简完全的扰动算子的表达式及相关的误差界．

在本文中，符号‖∙‖表示算子A的谱范数．记Aπ=I-ADA为A的对应于特征值0的特征投影．简记AnD=(An)D=(AD)n，n≥1．若A是(1)中的形式，那么‖AAD‖=‖Aπ‖=1．设||A||＜1，则I±A可逆且

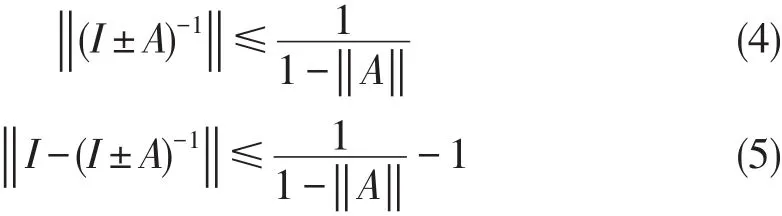
下面给出文中要用到的几个引理．

引理1[2-3]设H,L是两个Hilbert空间，A∈B(H)与B∈B(L)是Drazin可逆的，其指标分别为ind(A)=r，s=ind(B)且C∈B(L,H)，令，则M是Drazin可逆的且

引理2[4-5]设A,E∈B(H)是Drazin可逆的，且AE=0．

①若A是指标为r的幂零算子，则(A+E)D=；

② 若E是指标为s的幂零算子，则(A+E)D=

下面论述本文的主要结果．

定理1设A,E∈B(H)，A是Drazin可逆的且ind(A)=k，B=A+E，‖ADE‖＜1，则

若ADEAπEAD=0与ADEAπBAπ=0，则B是Drazin可逆的且

其中s=ind(AπBAπ)．

证明：因为ind(A)=k，算子A与E的矩阵形式分别为(1)、(3)，因此B的矩阵形式为

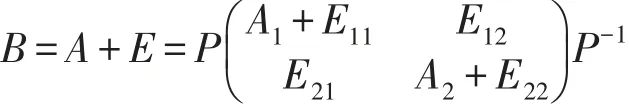
其中A1为可逆算子，A2为幂零算子且指标为k．

由 ‖ADE‖＜1得I+ADE可 逆 且I+ADE=，由此得I+A-11E11可逆，即A1+E11可逆且由引理1有-1

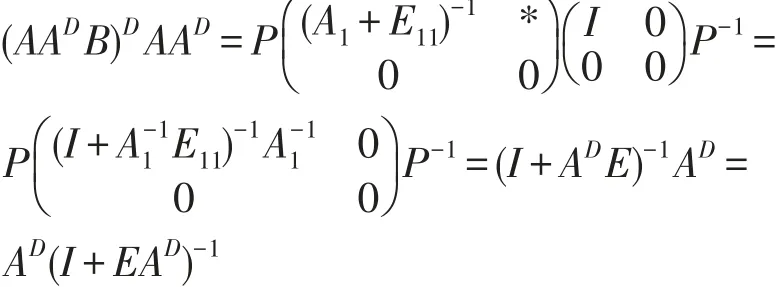
类似地可证AAD(BAAD)D=AD(I+EAD)-1与

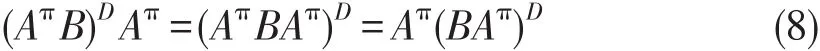
由(1)～(3)与ADEAπEAD=0可得E12E21=0．同理，由ADEAπBAπ=0可得E12(A2+E22)=0．令

计算可知RQ=0与R2=0，由引理2式(1)有

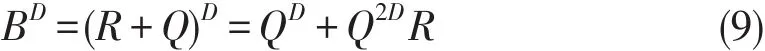
又由引理1有

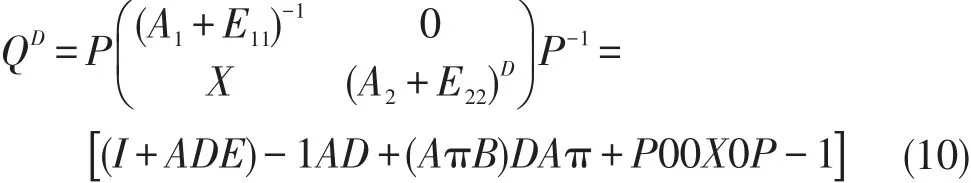
其中

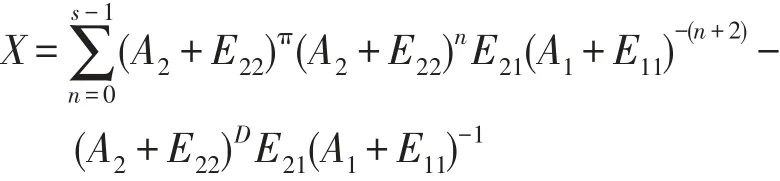
且s=ind(A2+E22)=ind(AπBAπ)．所以对任意的k≥s，

由(8)可得(AπB)π(AπB)kAπ=0．那么

将上式代入(10)中，由

与(6)有

由此可推出

因此由(9)与(I+ADE)-1ADE=I-(I+ADE)-1可得

定理2设算子A,E满足定理1的条件，则

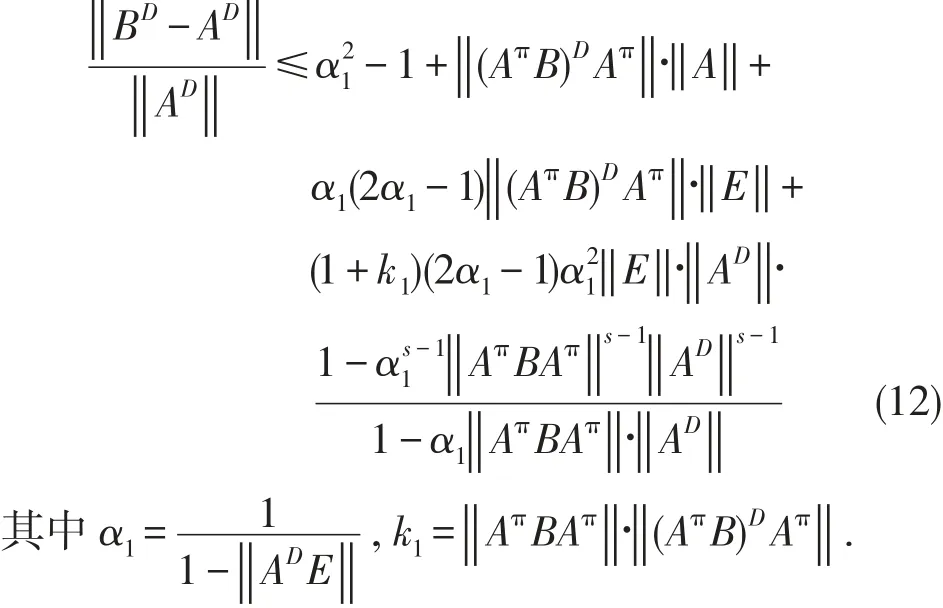
证明：因为(I+ADE)-1=I-ADE(I+ADE)-1，由(7)得

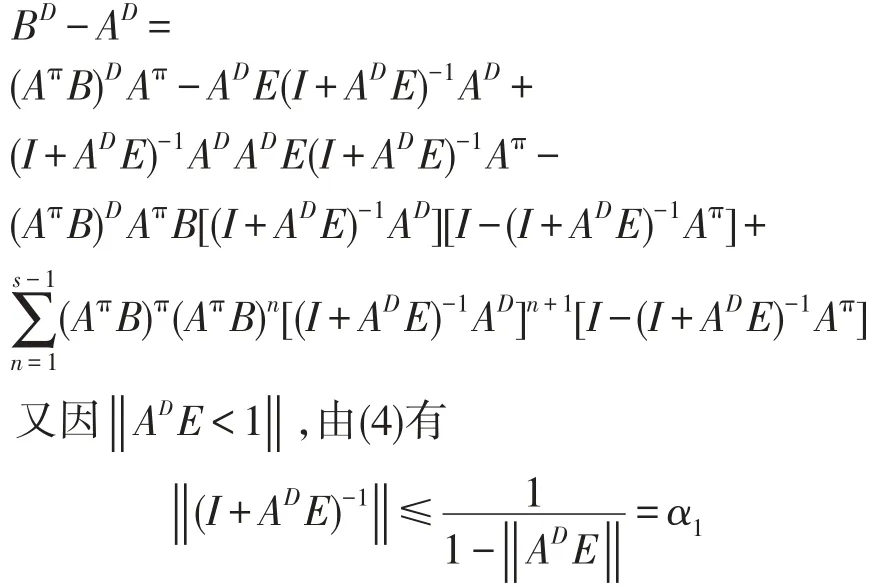
那么

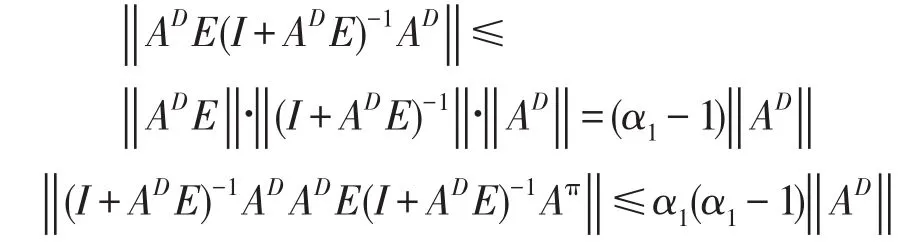
且由(5)有

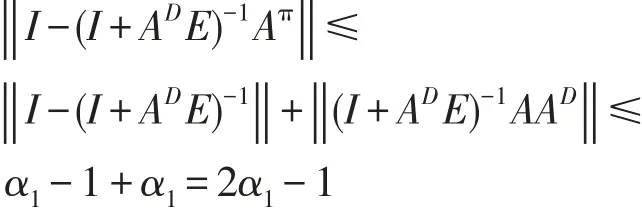
由(6)与(11)有

又有

因此

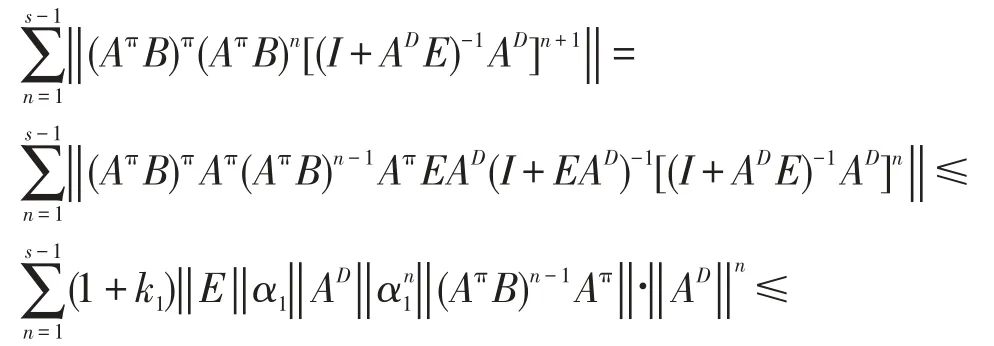
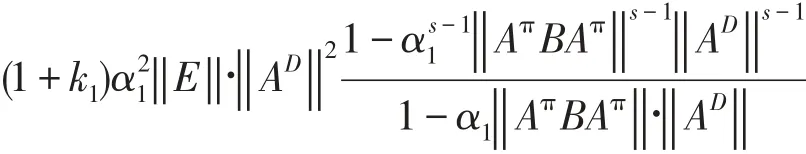
所以综合以上各式，得

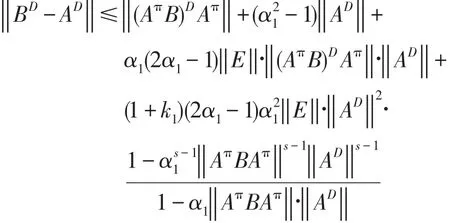
又因1=‖AAD‖≤‖A‖∙‖AD‖，所以由上式可得(12)．

若E=AADEAAD，即EAπ=AπE=0成立，满足定理1中的条件，由(1)～(3)式易得以下推论，并且以下推论在文[6]中已经证明对矩阵的情况是成立的．

推论1设A,E∈B(H)且ADrazin可逆，B=A+E.若E=AADEAAD，‖ADE‖＜1，则B是Drazin可逆的且

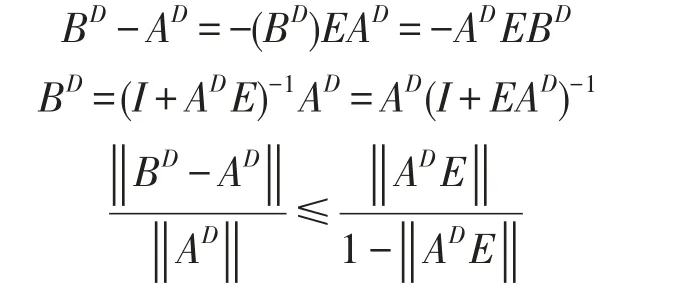
推论2设A,E∈B(H)且ADrazin可逆，B=A+E.若E=AADEAAD，‖AD‖∙‖E‖＜1成立，则B是Drazin可逆的且

[1]杨凯凡,杜鸿科.扰动算子的Drazin可逆性及其Drazin逆的表达[J].数学学报,2010,53(6):1187-1192.

[2]Meyer C D,Rose N J.The index and the Drazin inverse of block triangular matrices[J].SIAM J Appl Math,1977,33:1-7.

[3]Djordjevic D S,Stanimirovic P S.On the generalized Drazin inverse and generalized resolvent[J].Czechoslovak Math J,2001,51(126):617-634. [4]Hartwig R E,Wang G,Wei Y.Some additive results on Drazin inverse [J].Linear Algebra Appl,2001,322:207-217.

[5]Djordjevic D S,Wei Y.Additive results for the generalized Drazin inverse[J].J Austral Math Soc,2002,73:115-125.

[6]Wei Y,Wang G.The perturbation theory for the Drazin inverse and its applications[J].Linear Algebra Appl,1997,258:179-186.

【编校：许洁】

The Perturbation of the Drazin Inverse of Bounded Linear Operators

WU Shuxia
(Department of Mathematics,Sichuan University for Nationalities,Kangding,Sichuan 626001,China)

The sufficient conditions and expression for the Drazin inverse of the perturbed were derived.And the bound of the relative error was given based on the expression.

Drazin inverse;operator matrix;perturbation;norm

O177.6

A

1671-5365(2014)06-0010-03

2013-11-26修回：2013-12-26

四川民族学院科研项目(12XYZB007)

武淑霞(1985-)，女，助教，硕士，研究方向为矩阵(算子)的广义逆理论

时间：2013-12-30 11:58

http://www.cnki.net/kcms/detail/51.1630.Z.20131230.1158.004.html