b-度量空间中弱压缩映射的强收敛定理
2014-08-10刘信东
刘信东
(宜宾学院数学学院,四川宜宾644007)
b-度量空间中弱压缩映射的强收敛定理
刘信东
(宜宾学院数学学院,四川宜宾644007)
定义了b-度量空间中弱压缩映射,证明了由Picard迭代生成的序列强收敛到弱压缩映射的一个不动点.改进和推广了Fatma等人的研究结果.
b-度量空间;弱压缩映射;Picard迭代;不动点
Banach压缩映射原理自诞生以来,一直受到许多学者的亲睐,他们为此付出了大量的心血,对定理作了各种推广.最近,Fatma[1]将其推广到锥度量空间中的弱压缩映射,证明了该映射有不动点.作为度量空间的推广,b-度量空间越来越受到学者的重视,对度量空间中压缩映射作了大量的推广[2-5].
1 预备知识
定义1[2]设X是一个集合,s≥1是一给定实数. d:X×X→[)
0,∞是一个映射,如果对任意x,y,z∈X,有
(1)d(x,y)=0当且仅当x=y;
(2)d(x,y)=d(y,x);
(3)d(x,y)≤s[] d(x,z)+d(z,y).成立,则称(X,d)是一个b-度量空间.
定义2(X,d)是一b-度量空间,T:X→X是一个映射.如果存在a∈[0,1),b∈[0,∞),使得对任意x,y∈X有
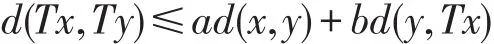
成立,则称T是一个弱压缩映射.特别地,当b=0时,称T为压缩映射.
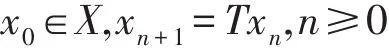
设T是一个弱压缩映射,本文的目的是考虑Picard迭代:证明该迭代生成的序列{xn}强收敛到T的不动点.改进和推广了Fatma等的结论.
2 主要结果
定理1设(X,d)是一个完备的b-度量空间,T:X→X是一个弱压缩映射.如果,则由Picard迭代所生成的序列{xn}是一个Cauchy列.
证明:对任意的n≥1,有
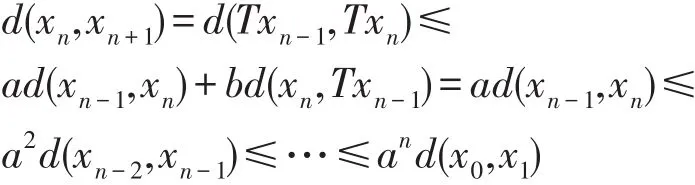
因此,对任意p≥1,有

定理2设(X,d)是一个完备的b-度量空间,T:X→X是一个弱压缩映射.如果则T有不动点.
证明:设{xn}是由Picard迭代所生成的序列,由定理1知,{xn}是一个Cauchy列.由于(X,d)完备,则{xn}收敛.设xn→z,(n→∞),下证z是T的不动点.
由于xn→z,(n→∞),则对任意 ε>0,存在N∈N+,使得n≥N,有于是
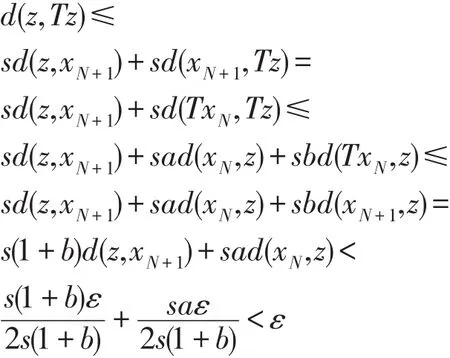
由ε的任意性知d(z,Tz)=0,则Tz=z,即z是T的不动点.
推论 设(X,d)是一个完备的b-度量空间,T:X→X是一个压缩映射.如果,则T有不动点.
[1]Fatma A S.Fixed point theorems for weak contractions in cone metric spaces[J].Int Journal of Math Analysis,2010,7(48):2367-2372.
[2]Razani A,Bagherboum M.Convergence and stability of Jungck-type iterative procedures in convex b-metric spaces[J/OL].Fixed Point Theory and Applications 2013,2013:331.http://www.fixedpointtheoryandapplications.com/content/2013/1/331.
[3]Bakhtin I A.The contraction mapping principle in almost metric spaces [J].Funct Anal,Gos Ped Inst Unianowsk 1989,30,26-37.
[4]Czerwik S.Contraction mappings in b-metric spaces[J].Acta Mathematica et Informatica Universitatis Ostraviensis,1993,1:5-11.
[5]Czerwik S.Nonlinear set-valued contraction mappings in b-metric spaces[J].Atti Semin Mat Fis Univ Modena Reggio Emilia,1998,46: 263-276.
【编校:许洁】
A Strong Convergence Theorem for Weak Constractive Mappings in B-Metric Spaces
LIU Xindong
(School of Mathematics,Yibin University,Yibin,Sichuan 644007,China)
In b-metric space,weak constraction was introduced.The sequence generated by picard iterative strongly converge to a fixed point of weak constraction.The result extends and improves the corresponding results announced by Fatma etc.
b-metric space;weak contractive mapping;picard iterative;fixed point
O177.91
A
1671-5365(2014)06-0016-02
2014-01-05修回:2014-01-20
宜宾学院青年基金资助项目(2007Q22)
刘信东(1975-),男,讲师,硕士,研究方向为泛函分析
时间:2014-03-28 17:12
http://www.cnki.net/kcms/detail/51.1630.Z.20140328.1712.003.html
