基于惩罚费用的城市轨道交通乘务排班优化模型与算法
2014-08-08张增勇毛保华吴珂琪
张增勇,毛保华,杜 鹏,许 奇,吴珂琪
(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京100044)
基于惩罚费用的城市轨道交通乘务排班优化模型与算法
张增勇,毛保华*,杜 鹏,许 奇,吴珂琪
(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京100044)
乘务排班计划是城市轨道交通运营的核心问题之一.本文首先分析了乘务排班问题,接着基于惩罚费用构建了乘务排班优化模型,并提出了相应惩罚费用计算方法.根据乘务排班计划步骤可知,模型分为乘务作业段生成模型和乘务工作班生成模型,其中乘务作业段生成模型为乘务工作班生成模型的下层,乘务作业段生成模型的解为乘务工作班生成模型的输入条件.随后针对建立的双层模型,分别设计了改进的Dijkstra算法和离散粒子群算法.最后,采用某地铁线路的运行数据对模型和算法进行了验证.结果表明,间休时间的均值为37分,工作时间的均值为6小时41分,并且所有的乘务工作班分布均匀,证明了模型与算法的有效性.
城市轨道交通;乘务排班计划;作业段;工作班;离散粒子群算法
1 引 言
乘务计划是城市轨道交通运营中的重要环节,主要解决轨道交通司机的值乘问题.国内多数城市的乘务计划由各线路乘务中心手工编制完成,一般消耗数周时间.为应对安全事故引起的能力变化,以及大型活动引起的客流波动,需要预制多个方案或者提前编制临时乘务计划.这种形式存在灵活性较差、对突发情况应变能力弱等问题,进而影响到城市轨道交通的运营效率与服务水平.
从编制内容上看,城市轨道交通乘务计划可分为乘务排班与乘务轮班两大部分,其中乘务排班是重点.国外关于乘务排班计划有一系列的研究成果,主要在国铁方面.乘务模型以集合覆盖和集合分割为主,求解算法多采用列生成技术,以及基于列生成技术的分支定价算法[1-3].国内关于乘务计划自动编制的研究主要集中在国家传统铁路、客运专线,以及高速铁路等[4-6].Chu、李献忠等[7,8]研究了基于智能算法的城市轨道交通乘务计划编制模型.陈仕军与沈吟东研究了公交排班问题[9].
求解乘务排班问题涉及条件众多,条件自身的变通性差,求解难度较大.不同乘务环境下的乘务排班模型及其求解方法也有所差异.鉴于此,本文首先分析了乘务排班问题,建立了乘务排班优化模型;提出了相关费用计算方法,构建了乘务作业段生成和乘务工作班生成的双层模型与求解算法;通过算例验证了模型和算法的有效性.
2 问题分析
按操作步骤,城市轨道交通乘务排班计划可分为列车运行任务分解、乘务作业段集合生成、乘务工作班集合生成三大部分.
从列车运行图中摘出的运行任务为不同车底执行的车次链集合,车次链为同一车底一次出、入车辆段或者停车场所执行的按时间顺序排列的车次集合.运行任务分解的节点为车辆段与值乘车站,分解后的片段称为乘务片段,可表示为

式中 n表示乘务片段编号,最大为N;r(k)表示第k个列车的车底编号,列车数最大为K;tS表示乘务片段的开始时刻;tE表示乘务片段的结束时刻;dS表示乘务片段的开始地点;dE表示乘务片段的结束地点;P表示乘务片段集合.
由同一车底中临近的一个或者多个乘务片段组成的片段集合为乘务作业段.乘务作业段可表示为
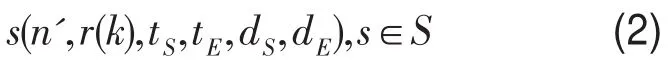
式中 n'表示乘务作业段编号,最大为 N',N'≤N;S表示乘务作业段集合.
乘务排班计划中,作业段集合方案是乘务排班方案的输入数据,乘务工作班作业段可以是不同的车底、不相关联的乘务作业段.一个乘务工作班可表示为

式中 n''表示乘务工作班编号,最大为N'',N''≤N';R(k)表示乘务工作班w中所包含的车底号集合;W表示乘务工作班集合.
3 模型构建
根据乘务排班步骤,本文构建了乘务作业段集合生成模型和乘务工作班生成模型,乘务作业段集合生成模型的解为乘务工作班生成模型的输入条件.在两层模型的构建中,求解目标均为与时间相关的广义费用.
3.1 费用计算方法
乘务排班相关的计算费用包括乘务作业段费用和乘务工作班费用两大部分.
(1)乘务作业段费用.
乘务作业段生成模型的费用为时间费用.一个乘务作业段由数个乘务片段组成,乘务作业段的费用表示为

式中 Tzh表示列车从车辆段发出时的整备时间标准;Tjb表示列车的交接班时间标准;α为0-1变量,乘务片段为段发时取1,否则为0;β为0-1变量,乘务片段为回段时取1,否则为0.
(2)乘务工作班费用.
乘务工作班费用为惩罚费用,按时间计算,并区分为不同值乘点间惩罚费用、间休时间惩罚费用、就餐惩罚费用、工作时间与作业时间惩罚费用.
①不同值乘点间惩罚费用.
不同值乘点间的惩罚费用可表示为

式中 Tijz表示不同值乘点间的走行时间标准,i、 j为交接班的两个值乘点的编号;a表示不同值乘点间值乘费用惩罚因子.
②间休时间惩罚费用.
间休时间的惩罚费用可表示为
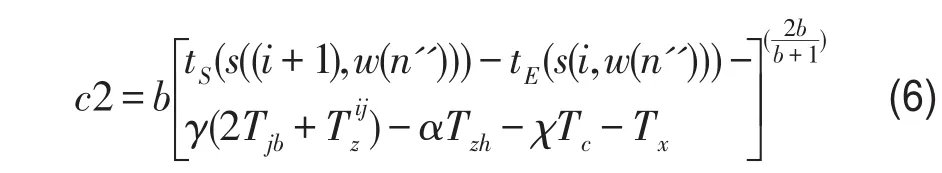
式中 b表示间休时间惩罚因子;Tc表示司机就餐时间长度的标准;Tx表示间休时间标准;γ为0-1变量,相邻乘务作业段为不同值乘点时取1,否则为0;χ也为0-1变量,相邻乘务作业段间存在就餐时间时取1,否则为0.
③就餐时间惩罚费用.
本文考虑的就餐时间[9]为午餐和晚餐,这两个时间的惩罚费用计算方法相同.惩罚费用计算时,就餐时间定为间休时间中靠近就餐正点的部分,其中,就餐时段为乘务排班过程中司机正常就餐的时间段(通常为:中午11点至13点、下午17点至19点),就餐正点Tzc为司机就餐的最佳时间(通常为:中午12点、下午18点).
就餐时间完全处于就餐时段内时,就餐时间惩罚费用为0.
就餐时间部分位于就餐时段外时,惩罚费用只计算时段外的部分.就餐时间在就餐正点前时,惩罚费用为
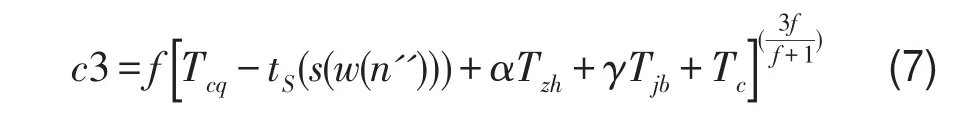
式中 Tcq表示就餐正点的最大前延时刻,就餐正点的最大后延时刻表示为Tch,最大前延时刻和最大后延时刻与正点的时间差距相同;f表示就餐时间惩罚因子.
就餐时间在就餐正点后时,惩罚费用为
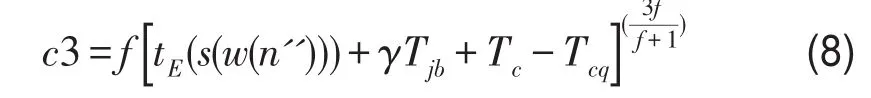
就餐时间完全处在就餐时段外时,惩罚费用按全部就餐时间计算.就餐时间完全在正点前时,有

就餐时间完全在就餐正点后时,惩罚费用为

④工作时间和作业时间惩罚费用.
工作时间惩罚费用为单向上限惩罚,即工作时间超限时进行惩罚.作业时间采用双向惩罚,即作业时间过长或者过短均进行惩罚.工作和作业时间的偏离采取两段式惩罚方案,一般地,工作时间有最长界定值,作业时间有最长和最短界定值.工作时间超出标准但在最长界定范围内计算惩罚费用,超出最长界定范围后计算加重惩罚费用.
对工作时间,超出标准时间,但仍在规定最长工作时间以内时,惩罚费用可表示为
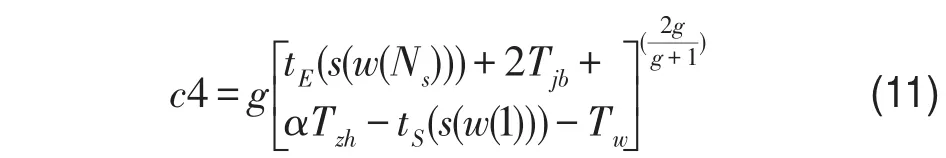
式中 g表示工作时间惩罚因子;Tw表示标准工作班时间长度;Ns表示一个乘务工作班中包含的乘务作业段数目.
超出规定最长工作时间后的加重惩罚费用为

式中 Twh表示工作班时间上限.
作业时间指司机在工作班内的实际劳动时间.平均工作量较大,在设计惩罚函数时,惩罚因子值可偏大一些.
对作业时间,超出标准作业时间,但仍在规定的上下界范围内,惩罚费用为

式中 h表示作业时间惩罚因子;Njb表示一个乘务工作班中包含的不同值乘点交接班数目;Nzh表示一个乘务工作班中包含的司机带车出段次数;Ty表示工作班中的作业时间总和标准.
超出作业时间上下界范围时,惩罚费用为

式中 Tyh为最长作业时间标准;Tyq为最短作业时间标准.
一个乘务工作班的总惩罚费用为

3.2 乘务作业段生成模型
乘务作业段生成模型目标函数为目标费用最小化:
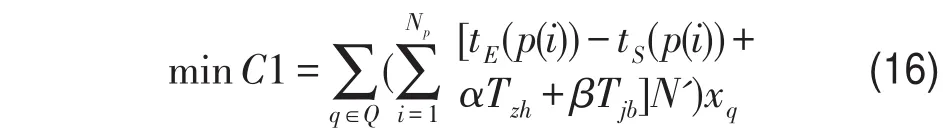
式中 q表示任一可行乘务作业段;Q表示所有可行乘务作业段的集合;xq表示0-1变量,q被选中时为1,否则为0.
约束条件如下:
(1)同一乘务片段仅允许在一个乘务作业段中出现,即
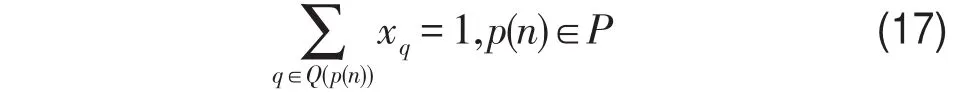
式(16)中,Q(p(n))表示包含乘务片段 p(n)的所有可行乘务作业段集合.
(2)同一车次链中任意两个乘务作业段的连续作业时间之和大于Ts,即
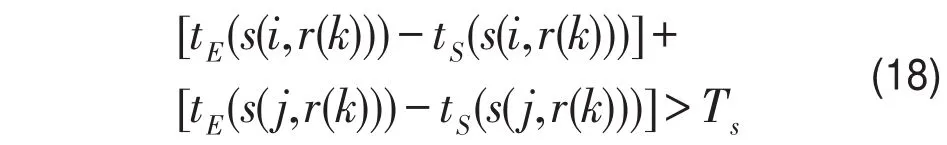
(3)同一个作业段中,相邻乘务片段间需满足

(4)同一个作业段中,所有乘务片段需满足
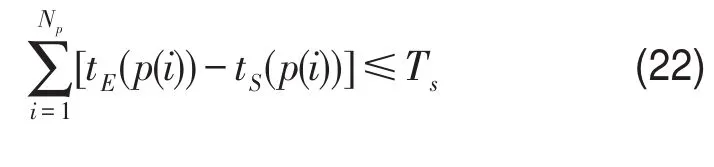
式中 Np表示乘务作业段中所包含的乘务片段数目.
3.3 乘务工作班生成模型
工作班生成模型目标函数为

约束条件包括:
(1)一个乘务作业段只能出现在某个乘务工作班中,即
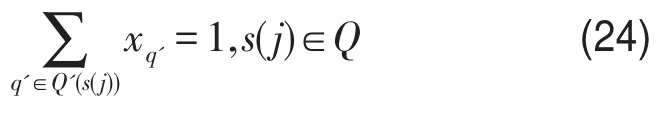
式中 Q'(s(j))表示包含乘务作业段s(j)的所有可行乘务工作班集合.
(2)乘务工作班中的间休时间不得小于Tx,即

(3)就餐时间长不得少于Tc,即

除上述约束外,若司机在执行某一工作班时,上班时刻早于 2Tcq-Tzc,同时下班时刻晚于2Tch-Tzc,则必须为该组司机在工作班中间预留就餐时间.
4 求解算法设计
针对构建的双层模型,下层模型采用改进的Dijkstra算法,上层模型采用离散粒子群算法.
4.1 乘务作业段生成算法
生成算法分为基本方案和方案调整两部分.
(1)基本方案.
具体操作步骤如下:
①将运行图中的运行任务按车底号依次摘出,得到一组车次链;这里,对某车底一天中多次出入段时视为多个车底的车次链,以标号区别.
②设置集合S=φ、集合P=φ、变量n'=1,将车次链分割得到的乘务片段以tS大小从1起依次编号,直到最大值N,将p置入S.
③从S中选取tS最小的乘务片段p(i),生成乘务作业段s(n');
④从S的剩余片段中搜索与s(n')同车底、时间最近的乘务片段 p(j),与s(n')组成新的乘务作业段s(n');
⑤重复步骤④,直到s(n')满足一个乘务作业段的条件,或者S中已无满足条件的乘务片段,将s(n')置入集合P,同时n'=n'+1;
⑥重复步骤③—⑤,直至S=φ,算法结束,否则转入步骤③.
上述过程得到的解为乘务作业段集合的初始方案,通过对初始方案的调整,产生新的方案,每一个方案为乘务工作班集合生成提供一次输入数据.
(2)方案调整.
乘务作业段方案调整以车次链为基础,同一车次链的乘务作业段为一组.若某车次链中存在乘务片段数少于均值的作业段,将其定义为小乘务作业段.一个车次链中只允许出现一个小乘务作业段.不存在小乘务作业段的车次链不进行调整;对于存在小乘务作业段的车次链以车底出段时间早晚分别编号为1,2,3,…,M.
乘务作业段集合方案调整过程可描述如下:
①设重新编号车次链的乘务作业段数为N,按时间早晚可依次编为1,2,3,…,N.小乘务作业段可分布在N个位次上;
②将1号车次链中的小乘务作业段分布在位次1上,按基本方案生成算法依次得到新的编号为2,3,…,N的乘务作业段,其他方案不变,此即为调整后的一个方案;
③依次调整1号车次链中的小乘务作业段分布位次为2,3,…,N,其他车底方案不变;
④调整2号车次链,将小乘务作业段依次分布在位次1,2,3,…,N上,针对每个位次,重复步骤②—③,剩余车底方案不变;
⑤调整3号车次链,将小乘务作业段依次分布在位次1,2,3,…,N上,针对每个位次,重复步骤②—④,剩余车底方案不变;
⑥按照步骤②—⑤的操作方法,依次调整编号为4,5,…,M的车次链中的小乘务作业段位次,直到所有的车次链中的小乘务作业段位次调整完.
4.2 乘务工作班生成算法
乘务排班问题的输入为乘务作业段集合方案,计算过程分为初始方案生成、寻优过程、算法结束三部分.
(1)初始方案生成.
初始方案生成计算同样采用改进的Dijkstra算法.
(2)寻优过程.
寻优过程采用离散粒子群算法,先对解集合空间Q'中的粒子位置和速度进行定义,如表1所示.

表1 粒子的位置和速度定义Table1 Definitions of a particle’s position and velocity
粒子的位置更新可表示为
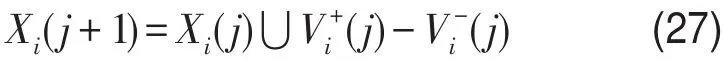
具体优化过程如下:
①用改进的Dijkstra算法生成I个初始解初始位置Xi(0);
②更新粒子Xi(j)的位置:首先将粒子中的乘务工作班根据作业时间(作业时间相同时,选择工作时间)从短到长依次编号为1,2,3,…,N'',计算Xi(j)的适应度值Ci(j),同时令n''=1;
③ 将 Xi(j) 中 组 合 为 工 作 班wi(n'',R(k),tS,tE,dS,dE)的数个乘务作业段重新分开,再将这些乘务作业段分别组合到剩余的乘务工作班上,组合原则为新生成的乘务工作班惩罚费用最小.计算分解—组合后的适应度值Ci'(j):
若Ci'(j)<Ci(j),则Ci(j+1)=Ci'(j),将 Xi(j)更新为Xi(j+1),V-i(j)为分解—组合前参与分解—组合的相关乘务工作班集合j)为之后相关的乘务工作班集合,粒子的当前最优位置LWi(j+1)=Xi(j+1),如果LWi(j+1)在I个粒子中的适应度值为最小值,则PW(j+1)=LWi(j+1),同时n''+1;
若Ci'(j)≥Ci(j),将分解的乘务作业段重新组合为wi(n'',R(k),tS,tE,dS,dE),粒子的其他值保持不变,粒子位置更新,同时n''+1;
④重复过程③,直到所有的乘务工作班均被分解—组合一次,即n''=N''+1时终止;
⑤对Xi(j)各粒子中的乘务工作班根据作业时间(作业时间相同时,选择工作时间)从短到长重新编号为1,2,3,…,N'',同时令n''=1;
⑥以粒子i中的wi(n'',R(k),tS,tE,dS,dE)为基础,依次与粒子中剩余工作班进行乘务作业段置换,原则为:降低乘务工作班惩罚费用,置换后的适应度为Ci'(j):
若Ci'(j)<Ci(j),则Ci(j+1)=Ci'(j),将 Xi(j)更新为Xi(j+1),(j)为置换前参与置换的相关乘务工作班集合,(j)为之后相关的乘务工作班集合,粒 子当 前 最优 位 置 LWi(j+1)=Xi(j+1);若LWi(j+1)在 I个 粒 子中适应度最小,则PW(j+1)=LWi(j+1).同时n''=n''+1;
若Ci'(j)≥Ci(j),将置换的乘务作业段重新回归原工作班,其他值保持不变,更新粒子位置,同时n''=n''+1;
⑦重复过程⑥,直到所有的乘务工作班均被置换验证一次,即n''=N''+1时终止;
⑧重复过程②—⑦,直到满足算法的结束条件为止.
(3)算法结束.
根据对迭代精度的要求终止寻优过程.具体操作为:当粒子在第J次迭代中相邻最优位置的适应度值之差小于PC时,算法终止.
5 算例分析
本文的算例为某地铁环线,含一个车辆段、一个值乘点;运行图数据共包括9列车,分为182个乘务片段,具体如表2所示.
相关的参数设置如表3所示.
根据表2和表3的相关数据,应用本文构建的模型与相应的算法,求得乘务排班的方案如表4所示.
从表4可以看出,乘务排班方案中包括30个乘务工作班、89个乘务作业段,存在2个内部含有不同值乘点交接班的工作班,1个只有2个乘务作业段的工作班.
乘务工作班中的间休时间反映了乘务排班方案质量优劣.本方案中,一个乘务工作班中平均含有2个间休时间段,其分布如图1所示.
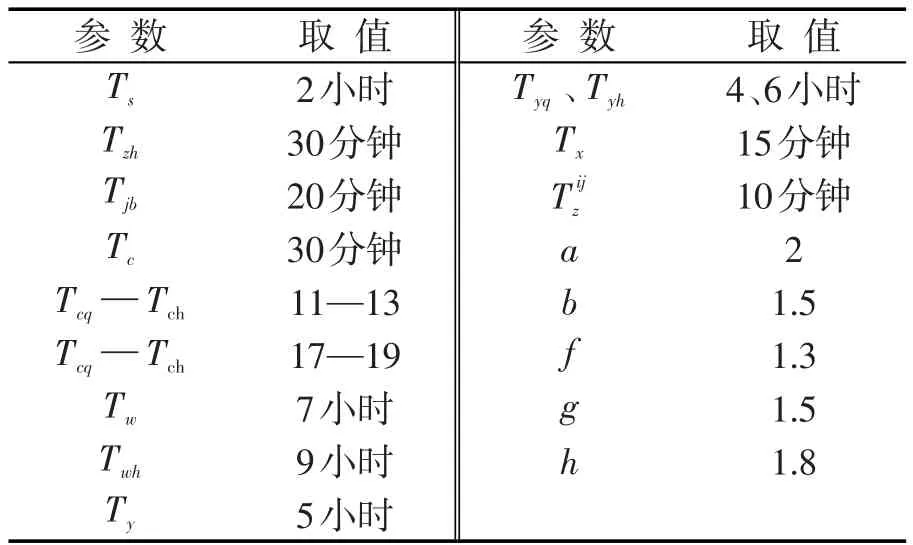
表3 参数取值Table3 Parameter value

表4 乘务排班方案Table 4 Crew scheduling results

图1 间休时间分布Fig.1 Rest time distribution
从图1中可以看出,间休时间长短相互穿插,依次递进.这说明不同时间段均存在编制较为困难的乘务作业段.从整体分布看,存在两个间休时间高峰,从表4可看出,乘务工作班均位于不同乘务工作班交接点、约束条件较多的区段,证明类似时间段内工作班编制较困难.
计算表明:间休时间1的平均值为42分,间休时间2的平均值为32分,平均超出标准间休时间22分.
工作时间、作业时间、间休时间是乘务排班计划方案的三个最重要指标,工作时间一定的条件下,作业时间与间休时间成反比.本方案中,工作时间、作业时间与间休时间的分布如图2所示.
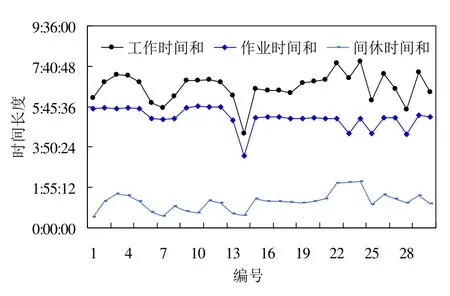
图2 工作时间、作业时间、间休时间分布Fig.2 Work time,operating time and break time distribution
算例中,工作时间均值为6小时41分,略低于标准值,这与算例中运行任务结构与模型惩罚机制有关.该算例一个工作班平均含有3个乘务作业段,时间约5小时.当一个工作班中含有4个乘务作业段,作业段时间之和将超过6小时;考虑间休时间、交接班时间等,一个乘务工作班实际时间将超过7小时.此外,模型中工作时间采取单向上限惩罚,故理论上工作时间均值将低于标准值,与算例中的计算结果相符合.
6 研究结论
良好的乘务排班计划可有效降低城市轨道交通企业运营成本.通过模型及算例发现:不同时间段均存在编制较困难的乘务作业段,尤其是在不同乘务工作班交接点、约束条件较多的时段;对工作时间及间休时间的整体分布分析表明,工作时间均值为6小时41分,低于标准工作时间19分钟;间休时间均值为37分,超出标准时间22分钟.此外,除了含有2个乘务作业段的工作班,剩余工作班的时间分布较均匀.这说明本文构建的模型与算法能够有效求解城市轨道交通乘务排班问题.
本文研究的是一般条件下的单交路城市轨道交通乘务排班计划优化方法,实际运营中,不同线路的乘务环境不同,比如不同客流分布条件、网络化运营条件等,采用的乘务计划编制方法不同,有待进一步地探讨.
[1]Dennis H.A column generation approach for the rail crew re-scheduling problem[J].European Journal of Op⁃erational Research,2007,180(1):163-173.
[2]Lucas P V,Daniel P,Dennis H,et al.Railway crew re⁃scheduling with retiming[J].Transportation Research Part C.2012,20(1):95-110.
[3]Silke J,Ulrich W T.Divide-and-price:A decomposi⁃tion algorithm for solving large railway crew scheduling problems[J].European Journal of Operational Research, 2012,219(2):214-223.
[4]赵鹏.高速铁路动车组和乘务员运用的研究[D].北京交通大学,1998.
[5]王莹,刘军,苗建瑞.客运专线乘务交路计划编制的优化模型与算法[J].铁道学报.2009,31(1):15-19. [WANG Y,LIU J,MIAO J R.Modeling and solving the crew scheduling problem of passenger dedicated line[J]. Journal of the China Railway Society,2009,31(1):15-19.]
[6]田志强.高速铁路乘务计划编制优化理论与方法研究[D].西南交通大学,2011.[TIAN Z Q.Study on theo⁃ry and methods of crew planning problem of high-speed railway[D].Chengdu:Southwest Jiaotong University, 2011.]
[7]Chu S C K,Chan E C.Crew scheduling of light rail tran⁃sit in Hong Kong:form modeling to implementation[J]. Computers Ops Res.1998,25(11):887-894.
[8]李献忠,徐瑞华.基于时问耗费的城市轨道交通乘务排班优化[J].铁道学报.2007,29(1):21-25.[LI X Z, XU R H.Optimization of crew scheduling for urban rail transportation based on time costs[J].Journal of the Chi⁃na Railway Society,2007,29(1):21-25.]
[9]陈仕军,沈吟东,苏璇,等.带中式用餐约束的乘务调度问题[J].交通运输系统工程与信息.2013,13(2):90-95.[CHEN S J,SHEN Y D,SU X,et al.A crew schedul⁃ing with Chinese meal break rules[J].Journal of Trans⁃portation Systems Engineering and Information Technol⁃ogy,2013,13(2):90-95.]
Urban Rail Transit Crew Scheduling Model and Algorithm Based on Punishment Costs
ZHANG Zeng-yong,MAO Bao-hua,DU Peng,XU Qi,WU Ke-qi
(Ministry of Education Key Laboratory of Complex System Theory and Technology of Urban Traffic,Beijing Jiaotong University,Beijing l00044,China)
Crew scheduling is one of the core issues of urban rail transit operations.This paper develops an optimization model of crew scheduling based on punishment costs,and proposes corresponding punishment cost calculation method.From the process of crew scheduling,it is found that the models include a crew operating segment generation model and a crew work shift generation model.The crew operating segment generation model is the lower model,and its results are the inputs of crew work shift generation model.Then,for the double-layer model,the paper formulates the improved Dijkstra algorithm and discrete particle swarm optimization.Finally,a subway line’s operational data are used to validate the model and algorithms.The results show that the average rest time is 37 minutes,the average working time is 6 hours 41 minutes,and the crew work shifts are uniformly distributed.All of these demonstrate the effectiveness of the models and its algorithms.
urban rail transit;crew scheduling;operating segment;work shift;discrete particle swarm optimization
1009-6744(2014)02-0113-08
U292.6
A
2013-12-05录用日期:2013-12-28
国家自然科学基金重点项目(71131001);国家基础研究计划项目(2012CB725406).
张增勇(1985-),男,山西运城人,博士生.*通讯作者:bhmao@china.com
