基于混合优化算法的磁聚焦线圈阵列设计与优化
2014-08-08杨龙成陆继庆刘腊梅
杨龙成,陆继庆*,张 帅,刘腊梅
(1.成都信息工程学院电子工程学院,四川成都610225; 2.戴氏教育精品堂培训学校,四川成都610100)
瞬变电磁法(TEM)[1-2]探测是地球物理探测的主要手段之一,通过向地下发射瞬变电磁信号,同时接收其产生的二次场,通过一定的反演算法来确定地下目标体的具体信息.利用瞬变电磁法探测地下目标体的技术已经被越来越广泛的应用[2-5].由于TEM系统普遍使用单个线圈作为发射回线,聚焦的区域范围过大、强度较小、深度较浅,不能对小区域进行准确的探测[4-5],并且在瞬变电磁检测技术中,线圈阵列的磁聚焦技术应用较少,对发射线圈阵列的磁场聚焦研究相对较少[6-9].
研究者们经过研究明确了线圈的各特性参数决定了探测的准确性和探测深度[6-9],所以要提高电磁场模拟的精度和实现磁场更好的聚焦性,则需要将线圈参数进行全面优化,逐步改善TEM发射线圈阵列的磁聚焦性能.本文设计新型的简单发射线圈阵列,对影响磁场分布的线圈可调参数进行分析,用高级语言编写的混合优化算法及其与有限元积分分析软件的外部通信接口,完成对发射线圈阵列的优化求解,达到改善目标区域磁场的聚焦效果.
1 圆形线圈模型
现有的发射线圈多采用圆形线圈,根据毕奥-萨伐尔定律,由磁场叠加定理得知,对于闭合的圆形线圈,假设线圈置于XOY平面,通过它的电流为Idl,该线圈在空间任一点P(x,y,z)感应的磁场为

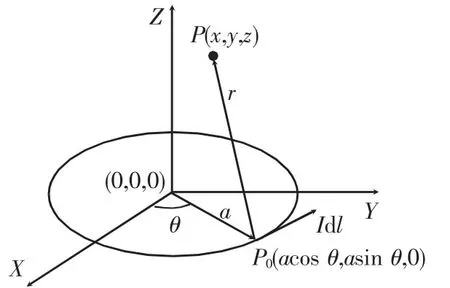
图1 圆形线圈计算模型Fig.1 Model for calculating the circular coil
图1中,a是圆形线圈的半径,Idl是线圈某一点P0处的电流元.r为电流元到P点的距离,θ是由线圈中心到P0点的矢径与X轴的正向夹角,且θ∈[0,2π).由文献[6-10]得P点处感应磁场B的矢量表达式
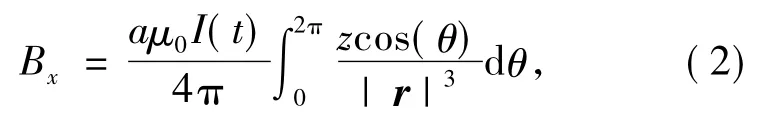

由(2)~(4)式可知,线圈在空间某一点P(x,y,z)产生的感应磁场强度B与线圈的半径a、通入线圈的电流大小I(t)以及P点的位置有关.磁感应强度影响磁探测深度,所以为了获得所需的磁感应强度,需要合理的设计线圈的尺寸和线圈相对于探测点的位置.希望磁场能量集中在小区域内,并且磁场强度越小越好.
2 线圈阵列模型设计
对于近些年许多线圈模型的研究与分析[6],本文以8字形线圈中电流汇聚实现磁场能量集中的特点为基础,综合分析构建了新型的8个子线圈.各子线圈圆心在XOY平面,且在同一圆环上平均分布,线圈平面与XOY平面垂直,在零点处各子线圈相接,线圈半径r取0.05 m,如图2所示.考虑子线圈个数对磁场聚焦性的影响,本文将子线圈个数增至20个,如图3所示.
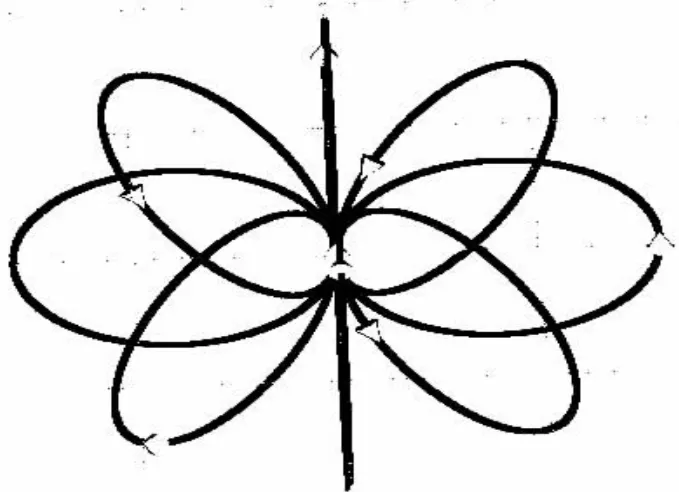
图2 8个子线圈的圆环线圈模型Fig.2 Eight coils ring coil model

图3 20个子线圈的圆环线圈模型Fig.3 Twenty coils ring coil model
3 混合优化算法设计
遗传算法[11]是模仿自然界生物进化过程与选择机制的随机搜索过程,不依赖搜索空间的具体领域限制,可高效率的解决复杂的非线性问题,具有较强的全局搜索能力,在最优解的搜索上有其独特的高效性,有很强的鲁棒性,但是收敛速度较慢,局部搜索能力明显不足.
粒子群算法[12]是一种基于群集智能、群体间相互合作的优化算法,模拟鸟群搜寻食物的行为.粒子追随自己的经验和全局最优粒子在空间进行全局搜索,粒子间的相互协作使粒子群算法具有较强的局部搜索能力,但粒子群算法缺少变异机制,算法陷入最优时较难跳出或是可能越过全局最优解.
针对2种算法的缺点,本文进行了改进.在遗传算法中,交叉变异算子均采用其值随着个体适应度值自适应改变[13]来保持种群的多样性和提高算法收敛最优解的性能;在粒子群算法中,引入惯性因子[14]来较好的控制粒子的搜索范围;引入收缩因子[15]来保证算法收敛.
因此通过融合不同的算法之间的优点来改进弥补算法自身的不足成为求解问题的一个重要有效的途径.本文设计了一种基于遗传算法的混合优化算法,主要在改进遗传算法的选择、交叉和变异操作后加入改进的粒子群算法的操作,使得混合优化算法在稳定性、全局搜索能力与局部搜素能力以及收敛速率都有较大的改善与优势.
3.1 参数选择采用改进的优化算法对2种线圈模型的线圈参数进行优化.由(2)~(4)式可知,当线圈半径和位置已经确定时,影响某一点磁感应强度的只有通入子线圈的电流和该点相对于线圈圆心的位置.因此算法对线圈模型的优化参数包括各子线圈的电流大小与方向和聚焦性较好的区域所处的平面位置2个方面.
1)个体编码:将逆时针方向的电流设为正值,顺时针方向的电流设为负值,本文设定电流范围为I∈(-2.56,2.56),本文设定的计算平面的范围为Z∈(0.05,0.20).
2)种群规模:根据适应函数值选取的一组解.
3)采用自适应交叉和变异策略.
4)最佳个体保留:本文将父代种群中适应度值最高的5%*N个体不经过选择、交叉、变异等操作直接复制到子代种群中,以保证优化过程中的优良解不被遗传算子破坏,而得以保留,加快了算法的收敛速度.
5)适应度函数:优化算法以适应度函数评估个体质量的好坏,如何将计算区域的磁场值转为适应度函数,是线圈模型优化的重点.本文设计的适应度函数为
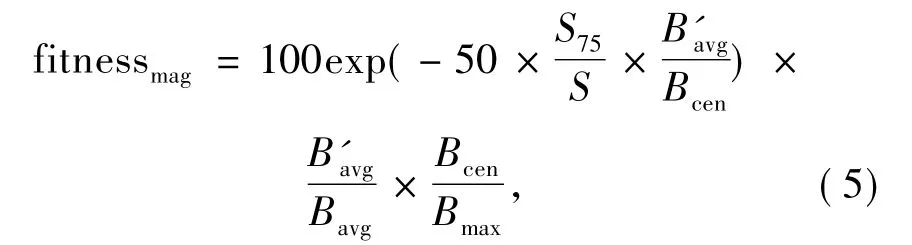
其中,Bcen为计算区域中心处的磁场,Bmax为计算区域的最大磁场值;S75为大于0.75倍Bcen所占的面积,S为整个计算区域的面积.以中心点为中心向外扩展选取5 cm×5 cm的小区域S1,希望磁场聚焦在S1内,设定S2=S-S1,S2中的平均磁场值为Bavg.当S2中存在大于0.75倍Bcen的磁场值时,将该磁场值设为0,进行以上处理后S2中的平均磁场值为Bavg.S75/S越小,表明磁聚焦性越好;B'avg/Bcen、B'avg/Bavg和Bcen/Bmax越大,表明磁场能量主要集中在中心区域.
3.2 混合优化算法与有限元积分分析软件数据通信线圈模型的优化对象主要是线圈的参数特性,如线圈的半径,注入线圈的电流及线圈的空间位置等.本文主要是用改进的混合优化算法优化发射线圈阵列,得到该线圈阵列的具体参数.线圈阵列模型的建立是利用有限元积分分析软件,那么要实现线圈阵列的优化参数必须将优化算法与有限元积分分析软件结合使用,有限元积分分析软件本身带有与外部Microsoft Visual C++6.0软件的接口,可以将这2种软件联合使用.本文根据实际线圈阵列的参数要求,混合优化算法与有限元积分分析软件数据通信的流程如图4所示.
3.3 三维坐标旋转依照上述模型,以数学理论为基础,编写程序对模型感应磁场分布进行计算.算法中每一代种群的每一个个体,若直接计算该个体在计算区域内每一网格点上的磁感应强度,计算极为复杂,整个程序运行速度很慢,因此本文引入坐标旋转的方式,大大简化了计算量.
空间各点的坐标变换用齐次坐标技术来描述,因此一系列的变换可以用矩阵形式表示.
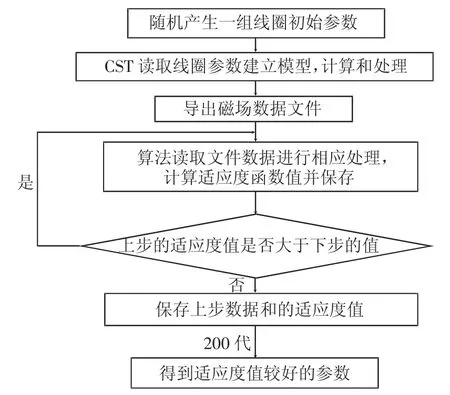
图4 CST软件与高级语言数据通信流程图Fig.4 Flow chart of data communication between CST software and a high-level language
1)平移变换.若三维坐标的平移量为(tx,ty,tz),用矩阵表示如(6)式所示.物体旋转的正方向是右手螺旋方向,即从该轴正半轴向原点看是逆时针方向.
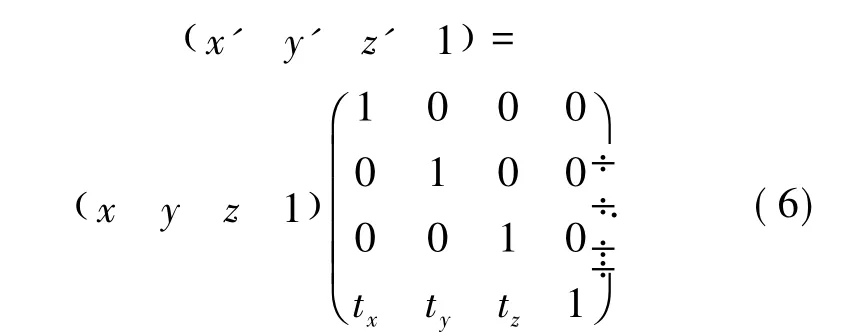
2)绕X轴旋转(假设旋转角度为θ,用矩阵表示)

3)绕Y轴旋转
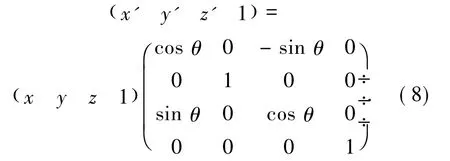
4)绕Z轴旋转
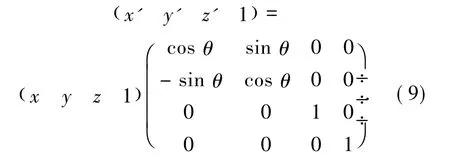
线圈模型在三维空间上具有对称性,将此种坐标转换的方法运用到空间磁场计算的程序的求解中,只需计算出单个线圈在网格平面上的磁感应强度.将各子线圈的感应磁场叠加,即可算出在电流的影响下线圈模型在计算平面内的磁感应强度.
4 优化结果与讨论
4.1 优化结果下面采用本文设计的混合优化算法分别对8个子线圈的圆环线圈模型和20个子线圈的圆环线圈模型在计算平面进行磁场聚焦性能进行优化,优化得出各子线圈的电流(A)大小为:8个子线圈的参数值 0.373、1.591、-0.227、1.832、1.65、0.574、-0.037、-0.781;20 个子线圈的参数值 1.612、1.767、-0.472、0.077、0.185、1.521、2.074、2.56,1.282、0.361、0.605、-0.877、0.663、0.916、2.256、0.681,1.373、0.832、-1.781、2.36,最优的Z平面为0.08 m,平面的优化结果如图5和图6所示.

图5 8个子线圈的圆环阵列模型在z=0.08 m处的感应磁场分布Fig.5 Magnetic field distribution established by eight coils ring array model in z=0.08 m

图6 20个子线圈的圆环阵列模型在z=0.08 m处的感应磁场分布Fig.6 Magnetic field distribution established by twenty coils ring array model in z=0.08 m
由图5和图6可以看出,本文对2种线圈阵列模型的磁聚焦优化有良好的效果,聚焦的平面很清晰,分布梯度很明显也很陡,并且磁场的87.5%及以上的能量集中在较小范围内,更加有利于定点刺激,较好的实现了磁聚焦.
4.2 讨论2种线圈模型在本文改进的算法的优化下,首先聚焦平面分布在一个比较直观的小区域内,则表明聚焦效果很好;其次磁场聚焦的能量分布梯度很陡,大部分的大能量值(磁场的87.5%及以上的能量)都集中在小范围内,则对于定点磁探测,大大减小了其他区域的干扰;最后,本文所显示的结果在位于聚焦平面的上方0.05~0.20 m的位置范围内,并且效果很明显,那么可以通过设置不同的区域或是平面高度,这就大大的改善了磁探测深度的效果.综上本文设计的模型与算法优化的结果,显示了良好的聚焦平面,很好的定点探测强度与较好的探测深度,说明基于混合优化算法的磁聚焦线圈阵列的优化设计取得了良好的效果.
比较本文设计的2种模型,发现20个子线圈组成的圆环阵列模型的磁场变化梯度更大,磁场能量主要集中在2 cm×2 cm的更小范围,基本上实现了点聚焦.因此增大子线圈个数,有利于增强子线圈接触点处的电流,从而增强磁场的聚焦性.
同时20个子线圈设计可实现非中心和多点聚焦(图6).说明通过调节注入各子线圈的电流大小与方向和聚焦性较好的区域所处的平面位置,可产生多种聚焦效果.这样就可根据使用要求调整其聚焦中心,扩大其应用范围.
5 结语
本文根据磁场的叠加定理,结合遗传算法与粒子群算法的基本特性设计了混合优化算法;用高级语言编程控制有限元积分分析软件,实现有限元积分分析软件与高级语言程序的数据通信接口及联合有限元积分分析软件件的TEM优化求解;对当前新型的线圈阵列模型中影响磁场分布的参数进行了讨论,采用坐标旋转方法与对称性简化了计算量,用优化算法优化了其中磁场分布集中且结构简单的模型,优化计算结果以归一化幅值分布和二维等高线图显示,表明在目标区域2种设计方案均可以很好地实现磁聚焦,同时20个子线圈模型还具备聚焦至多个及非中心点靶目标的能力,为全面优化发射线圈的空间结构研究提供了参考依据与实用价值.
[1]林君.电磁探测技术在工程与环境中的应用现状[J].物探与化探,2000,24(3):167-177.
[2]高永才,李永年,王绪本,等.瞬变电磁法金属管道腐蚀检测理论初探[J].物探化探计算技术,2005,27(1):29-33.
[3]石仁委,魏国栋,柳言国.埋地金属管道腐蚀剩余壁厚地面检测技术研究及应用[C]//济南:山东石油学会第三届腐蚀与防护技术学术交流会论文集,2005:132-143.
[4]李永年,陈德胜,尚兵,等.顺便电磁技术在检测管体缺陷上的应用研究[J].管道技术与设备,2003(4):27-29.
[5]杨勇,陈德胜,刘冀成,等.管道金属蚀失量检测聚焦信号加载理论研究[J].油气储运,2012,31(8):11-14.
[6]李景天,郑勤红.矩形线圈的磁场计算[J].云南师范大学学报:自然科学版,1997,17(1):60-64.
[7]刘冀成,黄卡玛,华伟.基于遗传算法的磁聚焦线圈设计与场分布计算[J].成都理工大学学报:自然科学版,2004,31(4):412-417.
[8]邝向军.矩形载流线圈的空间磁场计算[J].四川理工学院学报,2006,19(1):17-20.
[9]谭伟强,刘冀成,聂文亮.基于磁聚焦阵列的埋地金属管道腐蚀检测研究[J].油气储运,2013,32(5):536-539.
[10]冯亮,姚振东,刘冀成.经颅磁刺激引导源的设计[J].仪器仪表学报,2008,29(4):674-677.
[11]吕晋君.遗传算法的改进及其在优化上的应用研究[D].太原:太原理工大学,2010.
[12]刘晶晶.粒子群优化算法的改进与应用[D].武汉:武汉理工大学,2007.
[13]周鹏,贺威忠,林冬冬,等.经颅磁刺激电磁场分析系统设计[J].天津大学学报:自然科学版,2010,43(3):249-254.
[14]Shi Y,Ebethart R C.A modified optimizer[C]//Proc IEEE Congress on Evolutionary Compution,1998:69-73.
[15]刘晶晶,吴传生.一种带交叉算子的改进的粒子群优化算法[J].青岛科技大学学报,2008,29(1):77-79.
