一类高阶泛函微分方程非振动解的存在性

莫协强，张晓建，杨甲山

(1.梧州学院数理系，广西梧州543002； 2.邵阳学院理学与信息科学系，湖南邵阳422004)

关于中立型时滞泛函微分方程的振动和非振动的研究，除了在理论上具有非常重要的意义外，在实际应用中也有着非常重要的意义.因此，在这一领域出现了许多研究成果［1-17］.但是对于高阶中立时滞微分方程的非振动解的研究却受到了冷落，这主要是源自其分析上的技术困难.而具有正负系数的高阶中立型方程的非振动定理却更少了［6-14］.早些时候，M.R.S.Kulenovic等［2］研究了方程

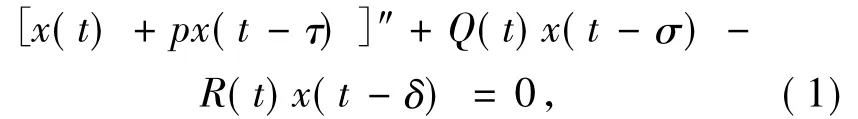
及“(H0):对每个t≥t0及任意常数α＞0均有αQ(t)-R(t)≥0”的条件下得到了方程(1)存在非振动解的结论.之后，如文献如［6-11］均围绕方程(1)，或p不是常数，或方程为非线性的变时滞的等，但都是在(H0)成立的条件下进行的研究，没有实质性的新进展.文献［12-14］的部分定理对条件(H0)有所改进，但没有方程的系统性的结果.本文旨在去掉这个强条件(H0)，讨论下列一类更广泛的具有正负系数的高阶非线性中立型时滞泛函微分方程

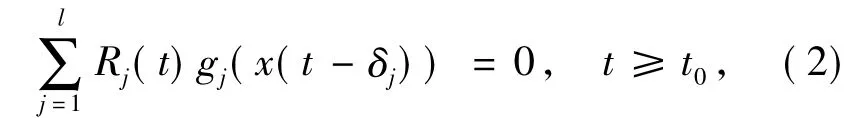
建立方程(2)非振动的若干新的准则，所得定理改进了现有文献中的一系列结论，并举例说明了定理的应用.这里n＞0 为偶数，τ＞0，σi≥0，δj≥0，t0＞0为实常数(i=1，2，…，m；j=1，2，…，l，后面出现的i，j其取值亦是如此，不再另外说明)；m≥1，l≥1 为正整数.

函数x(t)称为方程(2)的解，如果x(t)∈C(［t-1，+∞)，R)，x(t)+P(t)x(t- τ) ∈Cn(［t-1，+∞)，R)，并且x(t)满足方程(2)，这里t-1=min{t0- τ，t0-}.方程(2)在半直线［Tx，+∞)(Tx≥t0)上的解x(t)称为是正则的，如果它满足sup{|x(t)|:t≥T}＞0，∀T≥Tx.方程(2)的正则解称为是振动的，如果它有任意大的零点；否则，此正则解称为是非振动的.并考虑如下假设:

(H4)fi(x)、gj(x)均满足局部Lipchitz条件，即对于某区域D，存在常数Lfi(D)，Lgj(D)＞0，使得∀x，y≥0，有|fi(x)-fi(y)|≤Lfi(D)|x-y|和|gj(x)-gj(y)|≤Lgj(D)|x-y|；

(H4)'fi(x)、gj(x)均满足局部Lipchitz条件，即存在常数 α ＞0 及Lfi，Lgj＞0，使得∀0≤x≤α，0≤y≤α，有|fi(x)-fi(y)|≤Lfi|x-y|和 |gj(x)-gj(y)|≤Lgj|x-y|.

1 主要结果和证明

即此时(7)式是成立的.由数学归纳法知，(7)式得证.因此，根据(8)式，易知由(6)式所确定的x(t)是方程(2)的一个最终正解.定理证毕.

定理2设方程(2)满足条件(H1)～(H4)，0＜＜1，并且最终有P(t)≥0，则方程(2)一定存在一个非振动解.

注1由于本文例1中所给的方程均不满足条件(H0)，即不满足假设“对任意t≥t0及任意常数α＞0均有 αQ(t)-R(t)≥0”，因此文献［2，6-11］中的定理都不能用于本文例1的方程.从定理1～5的证明过程可知，方程(2)是否存在非振动解与条件αQ(t)-R(t)≥0是否成立并无必然联系.

注2当n为奇数时，用同样类似的方法可以证明，本文结论也是成立的.

［1］Tang X H，Yu J S.Positive solution for a kind of neutral equations with positive and negative coefficients［J］.Acta Math Sinica，1999，42(5):795-802.

［2］Kulenovic M R S，Hadziomerspahic S.Existence of nonoscillatory solution of second order linear neutral delay equation［J］.J Math Anal Appl，1998，228:436-448.

［3］Gai M J，Shi B，Zhang D C.Oscillation criteria for second order nonlinear differential equations of neutral type［J］.Appl Math J Chin Univ，2001，B16(2):122-126.

［4］Agarwal R P，Bohner M，Li W T.Nonoscillation and Oscillation:Theory for Functional Differential Equations［M］.New York:Marcel Dekker，2004.

［5］李秀云，刘召爽，俞元洪.具有正负系数的二阶中立型时滞微分方程的振动性［J］.上海交通大学学报:自然科学版，2004，38(6):1028-1030.

［6］王晓霞，仉志余.非线性二阶中立型时滞微分方程的非振动准则［J］.信阳师范学院学报:自然科学版，2001，14(1):16-21.

［7］李美丽，冯伟.二阶线性中立型时滞微分方程非振动解的存在性［J］.山西大学学报:自然科学版，2002，25(3):195-199.

［8］仉志余，王晓霞，林诗仲.非线性二阶中立型时滞微分方程的振动和非振动准则［J］.系统科学与数学，2006，26(3):325-334.

［9］Cheng J F，Annie Z.Existence of nonoscillatory solution to second order linear neutral delay equation［J］.J Sys Sci Math Scis，2004，24(3):389-397.

［10］Manojlovic J，Shoukaku Y，Tanigawa T，et al.Oscillation criteria for second order differential equations with positive and negative coefficients［J］.Appl Math Comput，2006，181(2):853-863.

［11］杨甲山.具有正负系数的二阶非线性中立型方程的非振动准则［J］.工程数学学报，2010，27(1):118-124.

［12］杨甲山.具有正负系数的二阶中立型方程的振动性定理［J］.华东师范大学学报:自然科学版，2011，2011(2):10-16.

［13］杨甲山，方彬.一类二阶中立型微分方程的振动和非振动准则［J］.四川师范大学学报:自然科学版，2012，35(6):776-780.

［14］杨甲山，孙文兵.一类多时滞二阶中立型微分方程的振动性［J］.中北大学学报:自然科学版，2012，33(4):363-368.

［15］郭振宇.关于一类新的高阶非线性中立时滞微分方程的非振荡解的存在性［J］.数学物理学报，2011，A31(5):1353-1358.

［16］杨甲山.具阻尼项的高阶中立型泛函微分方程的振荡性［J］.中山大学学报:自然科学版，2014，53(3):67-72.

［17］杨甲山，方彬.带最大值项的高阶非线性差分方程的非振动准则［J］.四川师范大学学报:自然科学版，2011，34(6):811-815.