(3+1)维ZK方程的孤波解、冲击波解和周期波解
2014-08-08康晓蓉鲜大权
康晓蓉,鲜大权
(西南科技大学理学院,四川绵阳621010)
本文研究如下形式的(3+1)维Zakharov-Kuznetsov(ZK)方程
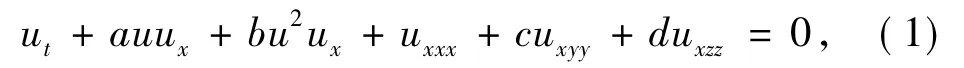
其中a、b、c、d为非零实数.20 世纪 80 年代末,Zakharov和Kuznetsov在描述磁化等离子体德尔演化过程中首次导出该模型,B.K.Shivamoggi等[1]用李群方法也得到该方程,A.M.Hamza[2]在强化等离子体的研究中则得到推广的(3+1)维ZK方程.该模型作为与波动现象密切相关的非线性方程,陆续出现在许多物理学领域,因此引起许多物理学家和数学家的关注.E.G.Fan等[3]用Jacobi椭圆函数法得到a=6,b=0,c=d=3时的N孤子解;杨红娟等[4]利用WTC方法讨论在一些特殊变系数情况下的一组精确孤波解;Z.Y.Yan[5]采用非线性方法得到系统的双周期波解、奇异波解等,并对所得解基于一些特殊参数值的非线性波传播特性进行分析,解释了相关物理现象;Z.Z.Dong等[6]应用经典Lie群方法获得方程的点对称,由此得到方程的一些精确解.但该方程作为高维系统的一个典型代表,它在不同可积性意义下的相应解结构有待研究的内容还很多,已尝试过的研究方法较少[1-6],而可用的方法尚多,如F展开法[7-8]、双曲函数法[9-10]、试探函数法[11]、扩展的G'/G展开法[12-13],等.
本文应用微分动力系统定性理论对方程(1)进行定性分析,并运用椭圆方程映射法寻求相应解的显式表达.
1 定性分析


容易看出λ1或为2不等实数,或为2共轭纯虚数,因此平衡点P1或为鞍点或为中心点.

则 λ2,3为2共轭复数,此时平衡点P2,3为焦点.
如果

则λ2,3或为2不等实数,或为2共轭纯虚数.此时平衡点P2,3或为鞍点或为中心点.
由(5)式可知,系统在相平面(ω,v)上的相轨线满足

积分(6)式得系统(5)的Hamiliton函数为

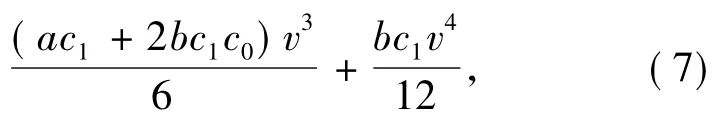
显然有,因此方程(4)所表达的系统为保守系统.
综上分析可得,系统(4)存在鞍-鞍同(异)宿轨和周期闭轨,(3+1)维ZK方程(1)相应地存在孤波解、冲击波解和周期波解[14].
2 孤波解、冲击波解和周期波解
下面用椭圆方程映射法寻求(3+1)维ZK方程(1)的孤波解、冲击波解和周期波解.
将(4)式乘以v'后再对ξ积分一次,取积分常数为A得


2.3 周期波解
2.3.1 Jacobi椭圆函数周期波解

这是围绕中心点的闭轨,且当m→1时,v3→v1,相应得到(1)式的周期波解为
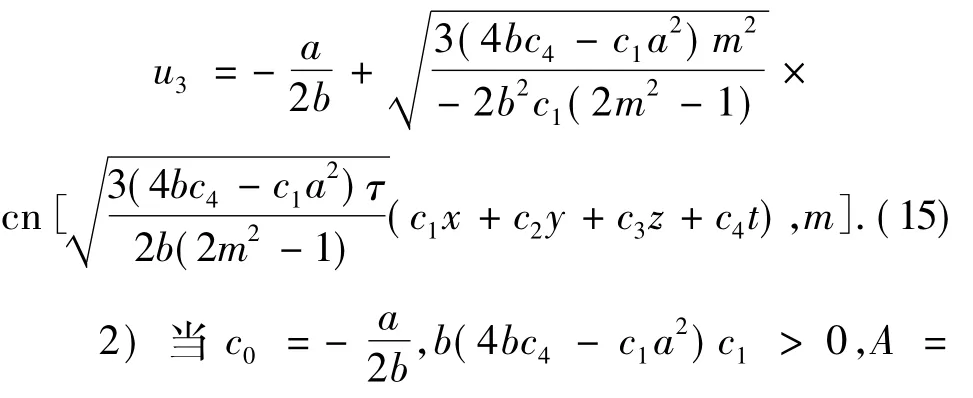

这是围绕中心点的闭轨,且m→1时,v3→v2.相应得到(1)式的周期波解

这是围绕中心点的闭轨,且m→1时,v5→v1,相应得到(1)式的周期波解为
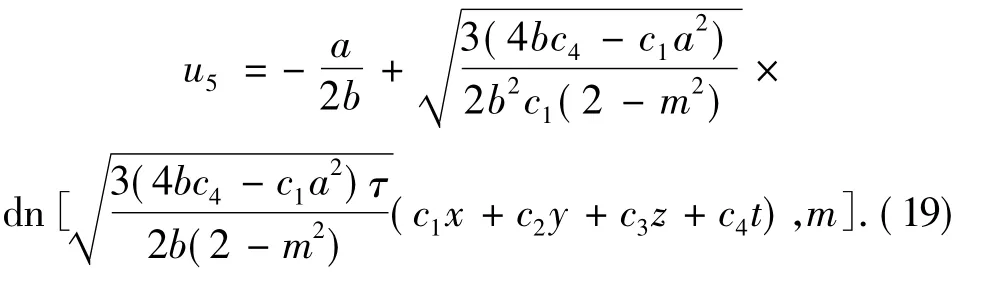
2.3.2 三角函数周期解 当A=0,,b<0且(4bc4-c1a2)c1<0时,

这也是围绕中心点的闭轨,相应得到(1)式的周期波解为

3 结论
本文应用微分方程动力系统定性方法讨论了(3+1)维ZK方程的鞍-鞍行波同(异)宿轨和周期闭轨的存在性.运用椭圆方程映射法获得该方程的孤波解、冲击波解和周期波解.本文的结果进一步丰富了该方程的数学物理性态及其解的内容.
[1]Shivamoggi B K,Rollins D K.Generalized painleve formulation of lie group symmetries of the ZK equation[J].Phys Lett,1991,A160:263-266.
[2]Hamza A M.Akinetic derivation of a generlized ZK equation for inacoustic turbulence in magnetized plasma[J].Phys Lett,1994,A190:309-316.
[3]Fan E G,Jian Z.Application of the jacobi elliptic function method to special-type nonliear equations[J].Phys Lett,2002,A305:383-392.
[4]杨红娟,吕克璞,段文山,等.变系数(3+1)维ZK方程的变速孤立波解[J].西北师范大学学报:自然科学版,2007,43(2):38-40.
[5]Yan Z Y.Periopdic,solitary and rational wave solutions of the 3D extended quantum ZK equation in dense quantum plasmas[J].Phys Lett,2009,A373:2432-2437.
[6]Dong Z Z,Chen Y,Lang Y H.Symmetry reduction and exact solutions of the(3+1)D Zakharov-Kuznetsov equation[J].Chinese Physics,2010,B19:9.
[7]蒋毅,陈渝芝,蒲志林.1+1维空间中变系数KdV方程组的精确解[J].四川师范大学学报:自然科学版,2007,30(6):670-673.
[8]田应辉,陈翰林.一类五阶非线性发展方程新的周期解[J].四川师范大学学报:自然科学版,2006,29(5):539-541.
[9]帅鲲,蒲志林.三维空间中Zakharov方程的精确解[J].四川师范大学学报:自然科学版,2010,33(4):433-436.
[10]蒋毅,蒲志林,孟宪良.三维空间中Klein-Gordon-Zakharov方程的精确解[J].四川师范大学学报:自然科学版,2007,30(3):262-265.
[11]赵云梅.利用试探函数法求耦合KdV方程的精确解[J].四川师范大学学报:自然科学版,2012,35(6):746-748.
[12]李灵晓,张金良.扩展的G'/G展开法和ZK方程的精确解[J].四川师范大学学报:自然科学版,2010,33(5):626-629.
[13]赵云梅.非线性耦合Schrödinger-KdV方程的新精确解[J].四川师范大学学报:自然科学版,2013,36(2):236-239.
[14]Xian D Q.Saddle-Node heteroclinic orbit and exact nontraveling wave solutions for(2+1)D KdV-Burgers equation[J].Abstract Appl Anal,2013,696074:1-7.
[15]Zhang S.A generalized auxiliary equation method and its application to(2+1)D KdV equations[J].Comput Math Appl,2007,54:1028-1038.
