次线性算子的多线性交换子在齐型Morrey空间上的有界性

赵 蕾，邓宇龙

(1.西藏大学理学院，西藏拉萨850000； 2.湖南科技学院数学与计算科学系，湖南永州425199)

为了研究二阶椭圆偏微分方程解的局部性质，C.B.Jr.Morrey［1］引 进 了 齐 型 Morrey 空 间Lp，λ(Rn)(1≤p＜∞，0＜λ＜n).Morrey空间在二阶椭圆微分方程解的局部性质研究中有着广泛的应用［2-3］.

交换子理论在算子理论研究中有极其重要的作用.A.P.Calderón［4］于1965 年研究了一类交换子，它出现在沿Lip曲线的Cauchy积分问题中［5］.R.Coifman等在文献［6］中证明了奇异积分交换子Tb的Lp(Rn)有界性.C.Pérez等［7］定义了奇异积分多线性交换子Tb(f)，且证明了Tb(f)的Lp(Rn)有界性.

本文主要讨论了次线性算子T与BMO函数生成的多线性交换子Tb在齐型Morrey空间上的有界性.得到了在Lp(Rn)有界的情况下，Tb是有界的.设次线性算子T:

其中，f∈L1(Rn)，f具有紧支撑且∀x■supp(f)，不等式

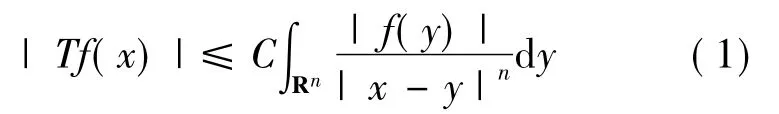
成立.在调和分析中有许多算子满足(1)式，例如Calderón-Zygmund 算子、C.Fefferman 奇异乘子、R.Fefferman奇异积分算子、Riui-Stein震荡积分算子、临界阶的 Bochner-Riesz算子等［8］.更多关于满足(1)式的次线性算子T和它的交换子Tb的研究参见文献［9-15］.

1 主要定理

2 定理的证明

［1］Morrey C B Jr.On the solution of quasi:linear partial differential equations［J］.Trans Am Math Soc，1938，43(1):126.

［2］Chiarenza F，Frasca M.Morrey space and Hardy-Littlewood maximal function［J］.Rend Math，1987，7:273-279.

［3］Fazio G D，Ragusa M A.Interior estimates in morrey spaces for strong solutions to nondivergence from equations with discontinuous coefficients［J］.J Funct Anal，1993，112(2):164.

［4］Calderón A P.Commutators of singular integral opertors［J］.Proc Nat Acad Sci USA，1965，53:1092-1099.

［5］ Calderón A P.Cauchy integrals on Lipschitz curves and related operators［J］.Proc Nat Acad Sci USA，1977，74(4):1324-1327.

［6］Coifman R，Rochberg R，Weiss G.Fractorization theorems for Hardy spaces in several variables［J］.Ann Math，1976，103:611-635.

［7］Pérez C，Trujllo-Gonzalez G.Sharp weighted estimates for multilinear commutators［J］.London Math Soc，2002，65:672-692.

［8］Lin Y，Lu S Z.Multilinear Calderon-Zygmund operator on Morrey type spaces［J］.Anal Theory Appl，2006，22(4):387-400.

［9］Fan D，Lu S Z，Yang D C.Regularity in morrey spaces of strong solutions to nondivergence elliptic equations with VMO coefficients［J］.Georgian Math，1998，5:425-440.

［10］曹俊峰，蔡宇泽.交换子在Morrey-Herz空间上的有界性［J］.苏州科技学院学报:自然科学版，2007，24(3):15-19.

［11］Tao S P，Wu J L，Sun X C.Boundedness for commutators on homogenceneous Morrey-Herz spaces［J］.J Mathematics，2009，29(1):21-26.

［12］徐莉芳.齐次Morrey-Herz空间上交换子的有界性［J］.北京师范大学学报:自然科学版，2004，33(3):10-14.

［13］Bandaliev R A.The boundedness of certain sublinear operator in the weighted variable Lebesgue spaces［J］.Czechoslovak Math J，2010，60:327-337.

［14］Guliyev V S，Aliyev S S，Karaman T.Boundedness of a class of sublinear operator and their commutators on generalized Morrey spaces［J/OL］.Abstract and Applied Analysis，2011，2011:356041.http://dx.doi.org/10.1155/2011/356041.

［15］王丽娟，束立生.一类次线性算子交换子在Morrey-Herz空间上的有界性［J］.南京大学学报:数学半年刊，2013，30(1):15-19.

［16］Lu S Z.Four Lectures on RealHpSpaces［M］.Singapore:World Scientific Publishing Company，1995.

［17］刘红海.Bochner-Riesz极大多线性交换子的有界性［D］.长沙:湖南大学，2007.