钢绞线网小偏心RC柱影响钢绞线用量因素分析★

高 淳 曹忠民 葛 超

(华东交通大学土木建筑学院，江西 南昌 330013)

钢绞线网小偏心RC柱影响钢绞线用量因素分析★

高 淳 曹忠民 葛 超

(华东交通大学土木建筑学院，江西 南昌 330013)

通过假定实际尺寸小偏压RC柱计算模型，对各个因素进行了计算分析，对比研究了各个因素对钢绞线用量的影响，得出影响钢绞线用量的三个主要因素分别为偏心距、钢绞线间距、柱长细比。

高强钢绞线网，聚合物砂浆，钢筋混凝土柱，小偏心，影响因素

高强度钢绞线网—聚合物砂浆加固技术是一种近几年发展起来的新型加固技术，21世纪初由韩国爱力坚公司研发，而后该加固技术传入我国，国内很多大学和研究单位对高强钢绞线网—聚合物砂浆的相关性能进行了大量的试验和数据分析[1-4]，并完成了实际工程的应用[5]。由于该技术涉及影响因素众多，而各个因素对钢绞线用量影响程度不同，本文通过计算分析并给出相应图表，提出对钢绞线用量影响较大的几个因素，以供工程实际和实验研究参考。

1 钢绞线网—聚合物砂浆加固小偏心受压RC柱承载力计算公式及分析

1.1 约束混凝土抗压强度计算

由于横向钢绞线网对混凝土柱的约束，约束混凝土的抗压强度将发生改变，考虑横向钢绞线数量、偏心距等参数对约束混凝土强度以及加固效果的影响，钢绞线网加固混凝土柱极限抗压强度的计算采用以下公式[6]：

fcc=fc+βγλw

(1)

其中，fc为混凝土抗压强度设计值；β为回归分析系数，对实验数据进行回归分析得β=72.64[7]；γ为偏心距影响系数，对于轴心受压构件(偏心距e0=0)，γ=1.0；对于纯弯构件(e0=∞)，γ=0.8；

(2)

λw为含钢绞线特征值：

(3)

其中，fw为钢绞线抗拉强度；s为钢绞线的间距；Aw为单根钢绞线面积；b′，h分别为柱截面宽度与高度。

1.2 等效柱宽及等效抗压强度的计算

根据钢绞线网对矩形柱的约束特点，建立相应受力模型[8]，把柱截面约束区域分为有效约束区域和非有效约束区域。非有效约束区面积Avn为：

(4)

其中，倒角半径r=15 mm；s为钢绞线间距，柱计算截面面积Av为：

Av=(b′-0.5s)(h-0.5s)-(4r2-πr2)-Ast

(5)

其中，Ast为纵向钢筋的总面积。有效约束区面积Ae为：

Ae=Av-Avn

(6)

由于薄弱面有效约束混凝土区域为不规则形态，为数值计算的便捷起见，将其等效为矩形区域，则等效柱宽b=Ae/h。

约束混凝土的等效强度fe采用以下计算方法：

(7)

1.3 小偏心受压混凝土柱承载力计算

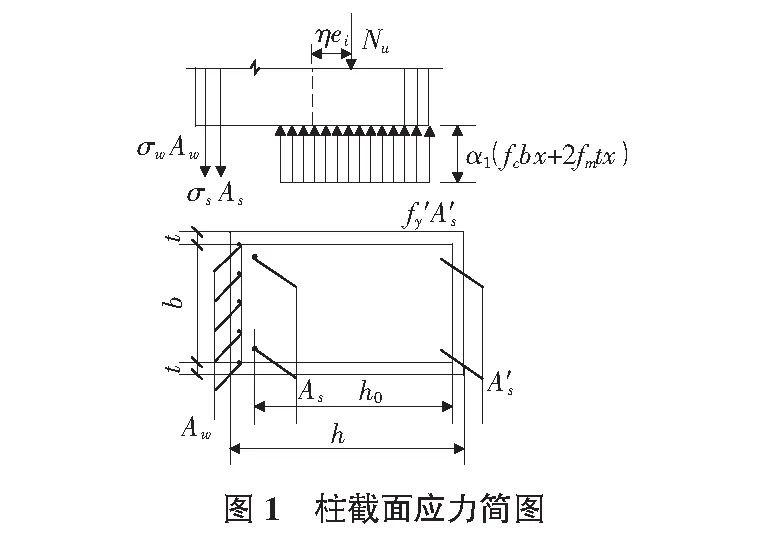
根据小偏心受压混凝土柱的受力状态(见图1)，由力和力矩平衡条件可得两个基本计算公式：

(8)

(9)

其中，Nu为钢绞线网—聚合物砂浆加固偏压钢筋混凝土柱承载力；fm为聚合物砂浆抗压强度；t为聚合物砂浆层厚度；n为受拉一侧钢绞线的根数；σw为钢绞线Aw的应力值；a′为受压纵筋中点到受压混凝土边缘距离；a为受拉纵筋中点到受拉混凝土边缘距离，当柱全截面受压时σw=0根据平截面假定，当部分受压时根据平截面假定计算可得：

(10)

其中，Ew为钢绞线弹性模量；Es为钢筋弹性模量；εcu为受压区边缘混凝土应变；σs为钢筋As的应力值；e为轴向力作用点至受拉钢筋As合力点的距离；σs和e均按规范公式计算[9]。

1.4 小偏心受压柱计算模型及钢绞线用量简化计算分析

初始计算模型采用500 mm×500 mm钢筋混凝土柱，偏心受压承载力N=5 000 kN，偏心距e0=70 mm，柱高h=3 m，柱长细比为6，纵向受力钢筋取HRB335 4φ28，纵筋配筋率ρ=0.985%，混凝土强度等级为C25，倒角半径r=15 mm，聚合物砂浆厚度t=20 mm，钢绞线间距s=30 mm，其他变量均按规范取值。

当构件处于小偏心受压时，根据平截面假定，截面受压区高度较大，钢绞线Aw的应力值σw很小，使得σwAw很小，从而σwAw这一项对于钢绞线配筋Aw影响不大，此时σwAw在计算过程中可以忽略不计。随着偏心距的增加，σw的取值将逐渐增大，则不能忽略其对钢绞线配筋的影响。为了说明这个界限，简化计算公式。在其他条件不变的情况下，改变偏心距，计算出忽略σwAw前后钢绞线用量值，进行对比：当相对偏心距e0/h0≤0.38时，Aw1/Aw≤1.1(Aw1为忽略σwAw项计算所得的钢绞线用量)，说明两者之间误差小于10%。此时计算时可以省略σwAw这一项。由计算可以得当柱处于界限破坏时，e0b/h0约为0.43。当0.38≤e0/h0≤0.43时，两者之间误差大于10%，则不能省略。说明在小偏心受压计算时，当在e0/h0<0.38即e0<180 mm的情况下，可以省略σwAw这一项进行钢绞线配筋计算，从而达到了简化计算公式的目的。

2 小偏心受压钢绞线用量影响因素分析

在小偏心受压计算中，影响钢绞线配筋量Aw的因素非常多，如钢绞线间距、混凝土强度、偏心距、长细比、倒角半径、砂浆厚度等。不同的因素对钢绞线配筋会产生不同程度的影响，本文采用单一变量原则,根据初始计算模型，选取6个变量进行分析，得出对配筋影响较大的几个因素。

2.1 偏心距对钢绞线用量的影响

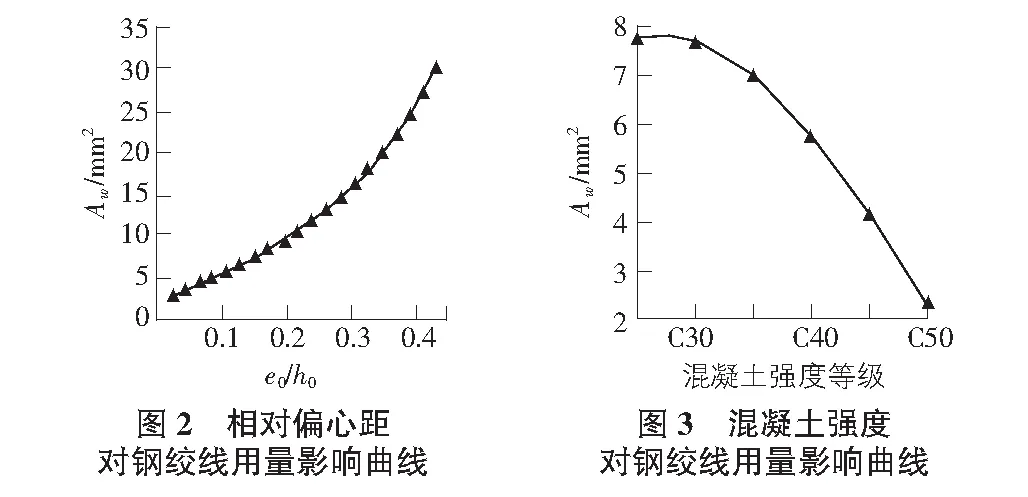
改变偏心距e0，其他因素不变，计算Aw并绘制相对偏心距变化引起钢绞线配筋变化曲线，见图2。

从图2中可以看出：小偏心受压时随着相对偏心距的增大，钢绞线用量也随之增大。随着偏心距增大，柱受拉侧竖向钢绞线开始发挥作用，因此钢绞线用量增加幅度较偏心距较小时有所增加。

2.2 混凝土强度等级对钢绞线用量的影响

改变混凝土强度，其他条件不变，计算Aw并绘制混凝土强度等级引起钢绞线配筋变化曲线，见图3。从图3看出：构件在小偏心受压时，随着混凝土强度的提高，所需钢绞线用量随之减少，可以得出混凝土对钢绞线用量的影响不是非常大，根据约束混凝土的计算公式，混凝土强度fc的改变引起约束混凝土等效强度fc的改变量并不大，导致最终对钢绞线配筋量Aw的影响没有预期大。

2.3 钢绞线间距对钢绞线用量的影响

改变钢绞线间距S，其他条件不变，计算并绘制钢绞线间距变化引起钢绞线配筋量变化曲线，见图4。从图4中可以看出：构件在小偏心受压时，随着钢绞线间距s的增大，钢绞线配筋量也随之增大，两者关系接近线性。

2.4 倒角半径对钢绞线用量的影响

改变倒角半径r，其他条件不变，计算并绘制倒角半径改变引起的配筋变化曲线见图5。从图5中可知：当r/h≤0.24时，倒角半径的增加可以使约束混凝土的面积增加，从而导致等效约束混凝土强度增加，使所需的钢绞线用量减少。当r=120 mm即r/h=0.24时，钢绞线用量达到最少。当r继续增加，由于截面面积被削弱过多使得钢绞线用量开始增加。

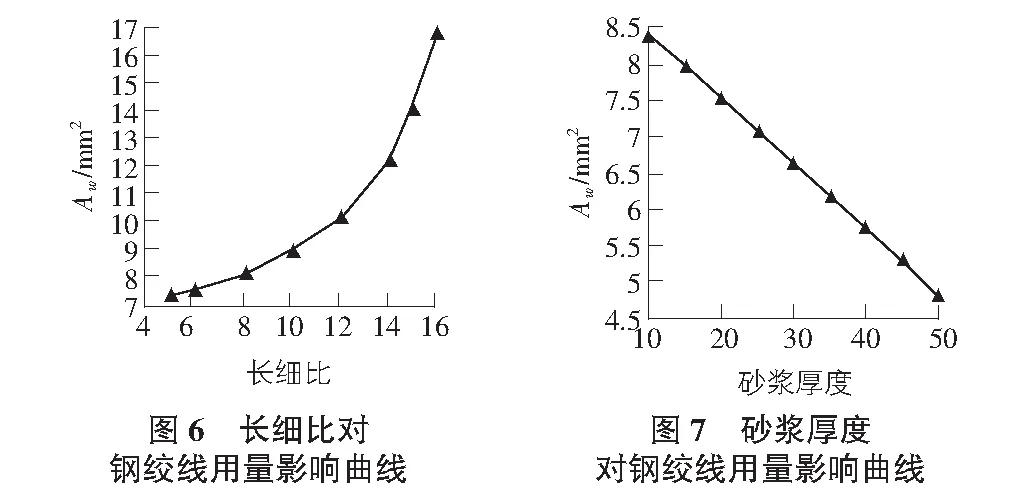
2.5 长细比对钢绞线用量的影响

改变柱长细比，其他条件不变，计算长细比改变时钢绞线配筋的变化量，并绘制相应曲线见图6。从图6中可得：构件在小偏心受压时，随着长细比的增大，弯矩增大系数也随之增大，间接引起弯矩的增大，从而使钢绞线配筋量增加。

2.6 聚合物砂浆厚度对钢绞线用量的影响

改变聚合物砂浆厚度t，其他条件不变，计算可得，随着聚合物砂浆厚度的增大，钢绞线配筋量逐渐减小，见图7。因为随着聚合物砂浆厚度的增加，对于构件承载力的贡献增大，钢绞线的用量也逐渐减少。但由于砂浆截面相对于混凝土构件截面较小，提供的承载力有限，则其对钢绞线配筋的影响也比较小。

2.7 小结

上述所取的6个影响因素变化均属于常规变化范围，综合以上图表，可以得到偏心距e0对钢绞线配筋量的影响最大，在实际工程或实验研究中，着重考虑偏心距、钢绞线间距、混凝土强度、长细比的影响。

3 结语

1)在计算高强度钢绞线聚合物砂浆加固小偏心RC柱的钢绞线配筋时，当e0/h0≤0.38时，忽略计算公式中σwAw项计算所得的Aw1相对于Aw误差小于10%，可以考虑忽略σwAw项简化计算公式。

2)对钢绞线用量影响最大的三个因素为：偏心距、钢绞线间距、长细比。在工程实际和实验研究中应该考虑偏心距、钢绞线间距、混凝土强度、长细比对于Aw的影响。倒角半径和聚合物砂浆厚度对结果影响不大，可以视情况考虑其影响。

3)方形截面柱控制倒角半径时，当r/h=0.24时，可以使钢绞线的用量达到最小，在一定程度上节约了钢绞线。

[1] 聂建国，王寒冰，张天申，等.不锈钢绞线网—渗透性聚合砂浆抗弯加固的试验研究[J].建筑结构学报，2005，26(2)：1-9.

[2] 曹忠民，李爱群，王亚勇，等.高强钢绞线网—聚合物砂浆抗震加固框架梁柱节点的试验研究[J].建筑结构学报，2006，27(4)：10-15.

[3] 张 蔚，李爱群，姚秋来，等.高强钢绞线网—聚合物砂浆抗震加固既有建筑砖墙体试验研究[J].建筑结构学报，2009，30(4)：55-60.

[4] 黄 华，邢国华，刘伯权，等.高强不锈钢绞线网—渗透性聚合砂浆加固梁抗弯承载力试验研究[J].工业建筑,2007，37(3)：106-110，119.

[5] 王亚勇，姚秋来，巩正光，等.高强钢绞线网—聚合物砂浆在郑成功纪念馆加固工程中的应用[J].建筑结构，2005(8)：41-43.

[6] 过镇海.钢筋混凝土原理[M].北京：清华大学出版社，1999.

[7] 潘晓峰.高强度钢绞线—聚合物砂浆加固小偏心受压混凝土柱的试验研究[D].南京：南京工业大学学位论文，2007.

[8] 刘伟庆，王曙光，何 杰，等.钢绞线网—聚合物砂浆加固钢筋混凝土柱的正截面承载力研究[J].福州大学学报(自然科学版)，2013，41(4)：456-462.

[9] GB 50010-2010，混凝土结构设计规范[S].

Influencing factors of reinforcement of steel wire in small eccentric RC column strengthed by steel wire mesh and polymer mortar★

GAO Chun CAO Zhong-min GE Chao

(CollegeCivilEngineeringandArchitecture,EastChinaJiaotongUniversity,Nanchang330013,China)

Through assuming calculation model of actual size small eccentric RC column, calculation and analysis of various factors, comparing the influence of these factors on the reinforcement of steel wire. Conclusion shows that three main factors influencing the reinforcement of steel wire are eccentricity, steel spacing and slenderness ratio.

high strength steel wire mesh, polymer mortar, RC column, small eccentric, influencing factors

1009-6825(2014)15-0030-03

2014-03-15★：国家自然科学基金资助项目(项目编号：51368019)

高 淳(1988- )，男，在读硕士； 曹忠民(1972- )，男，博士，副教授； 葛 超(1990- )，男，在读硕士

TU311

A