基于改进遗传算法的瑞利波频散曲线的反演

尹 丽 景海河 董连成

(黑龙江科技大学，黑龙江 哈尔滨 150022)

基于改进遗传算法的瑞利波频散曲线的反演

尹 丽 景海河 董连成

(黑龙江科技大学，黑龙江 哈尔滨 150022)

对勘探介质中参数对频散曲线的影响进行了探讨，提出了应用改进遗传算法反演Rayleigh波频散曲线的问题，针对青藏铁路北麓河场地进行了频散曲线的反演，验证了改进遗传算法的有效性，实验验证：利用改进遗传算法可对Rayleigh波频散曲线进行反演，提高了计算速度和精度。

介质，参数，遗传算法

随着经济科技的快速发展，高速铁路、跨江桥梁、城际铁路等大型建筑的建设对地基的要求更精准，必须查明土层的结构，以便在工程实践中及时有效的采取处理措施，降低危害。Rayleigh波[1]在传播过程中携带了丰富的地层介质信息，并与其传播速度与介质的物理力学性质密切相关，且具有分辨率高、无损、抗干扰能力强、效率高、衰减小且不受地层速度关系的优点，已被广泛应用于土层的物理力学参数原位测试、空洞探测、工程地质勘察、地基加固及公路无损检测等领域。通过反演Rayleigh波频散曲线可以获取介质层厚度和横波速度，精准判断场地信息，而且可进一步研究土层的泊松比、变形模量，压实度、抗压抗折强度、地基承载力等物理力学参数，因而如何准确可靠地反演瑞利波频散曲线就显得尤为重要[2]，作者从弹性多层介质出发，研究了介质参数对频散曲线的影响，探讨了遗传算法存在的不足和缺陷，如效率低，计算量大及收敛难等，限制了其在Rayleigh波反演等领域的更广泛应用。故而，作者提出了采用改进遗传算法[3]对频散曲线进行反演的问题，设计了反演方案，并针对青藏铁路北麓河场地进行了频散曲线的反演，反演结果验证了方法的有效性。

1 勘探介质参数对频散曲线的影响

Rayleigh波频散曲线是含有土层信息的重要曲线，是进行反演的必要前提。根据北麓河K1139+820场地钻孔资料(来自吴志坚“青藏铁路沿线冻土场地地震动特征研究”论文[4])，见表1，并借助于Rayleigh波频散函数进行相速度提取，结果见图1。

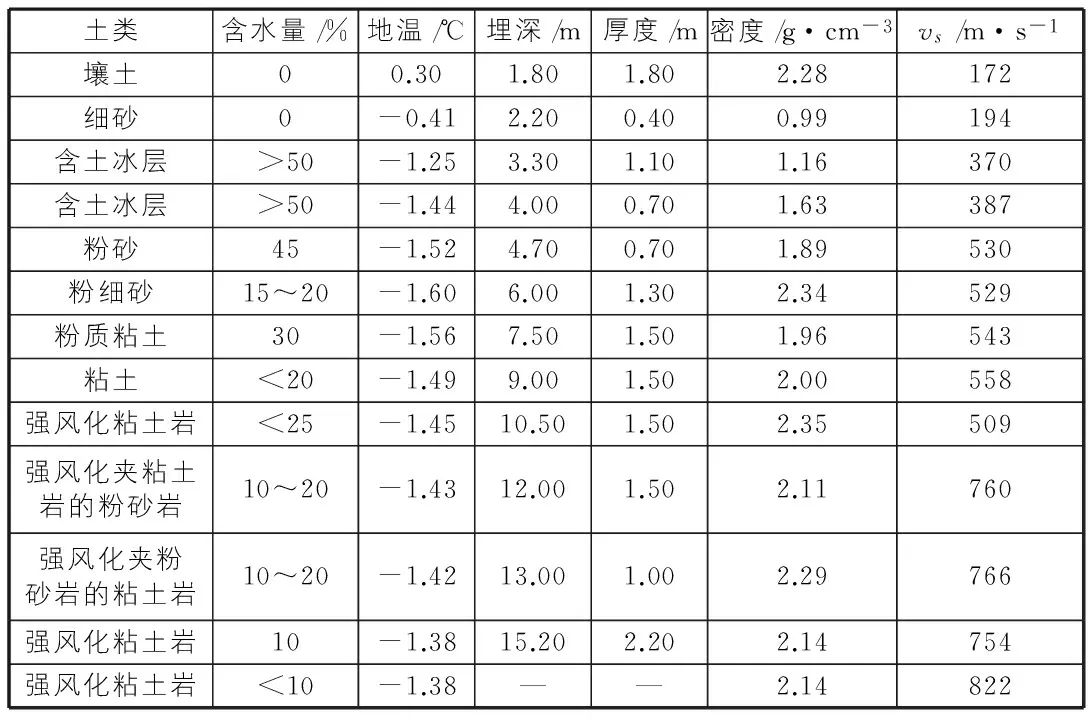
表1 场地钻探资料

在层状半空间介质中，假设m层土层参数有密度ρm，厚度Hm，拉梅常数λm，剪切模量Em，纵波速度Vpm，横波速度Vsm，Rayleigh波速度VRm，这些因素都是描述土层介质物理性质的重要参数。本小节考虑当其中一个土层参数增加5%时，频散曲线的变化，见图2。从图2中可以看出改变量相同的情况下，容重对频散曲线的影响最小，其次是泊松比、阻尼比，再者就是厚度，影响最大的就是剪切波速度。依据土层参数对频散曲线的影响，可以认为剪切波速度可以作为反演的目标。故考虑在进行反演分析时主要考虑剪切波速度和厚度。

2 改进遗传算法

在实际计算过程中发现，标准遗传算法很难收敛，效率很低，只有经过改进的遗传算法，才能够使算法的闪光点得以实现[5]。基于遗传算法的不足，本文提出适应度标定。利用这种方法进行选择，可以使个体之间的适应度值比保持较合理的差距，从而达到早期限制竞争、晚期鼓励竞争的目的。

动态线性适应度标定函数，见式(1)。

fk′=afk+b

(1)

其中，fk为标定前适应度函数；fk′为标定后的适应度函数。

为控制适应度最大的个体在下一代中的期望复制份数，故而需要设置最佳个体的期望复制份数。假设群体规模大小为50个～100个时，一般建议取1.2～2。

系数a，b满足式(2)。

(2)

a，b满足以下两个条件：

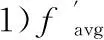
2)fmax=Cfmax。

其中，C为最佳个体的期望复制份数。

当适应度选择上使用线性定标后，改变了个体适应度之间的差距，维持了种群的多样性，并且计算简单，易于实现。线性定标的计算原理，如图3所示。

当群体内某个体的适应度远低于其他个体的适应度平均值，而此时fmax和favg值近似相等时，在这种情况下运用线性标定方法进行适应度函数定标，可能出现适应值为负的情况。为了避免最小适应度为负值，则需进行如下的变换：

(3)

根据上述讨论分析看出，最佳个体的期望复制份数C决定了适应度函数缩放程度。在传统的遗传算法中，C没有固定且通用的计算公式，选取具有不可预见性和随机性，存在影响全局最优化结果的隐患。因此，作者对C进行规定，假设C为关于进化代数的函数，并且使C值随进化代数的变化而变化，其关系式为：

C(k)=Cmax+kh

(4)

其中，k为当前进化代数；Cmin为C经验值的最小值；Cmax为C经验值的最大值；g为遗传代数；h=(Cmax-Cmin)/g。

由式(4)知，在进化初期，当出现个体分散明显时，较小的值能较大程度地缩小个体适应度的差距，具体见式(5)。

C(k)=Cmin+kh

(5)

3 Rayleigh波反演的实现

本节将各层的密度和纵波速度视为已知量，仅对各层的横波速度和厚度进行反演利用遗传算法、上述改进的遗传算法分别对青藏北麓河进行频散曲线反演，并将反演结果与标准遗传算法计算的结果进行对比分析。结果表明，改进的遗传算法有效地提高了收敛速度和反演精度。

具体反演参数的搜索范围见表2。

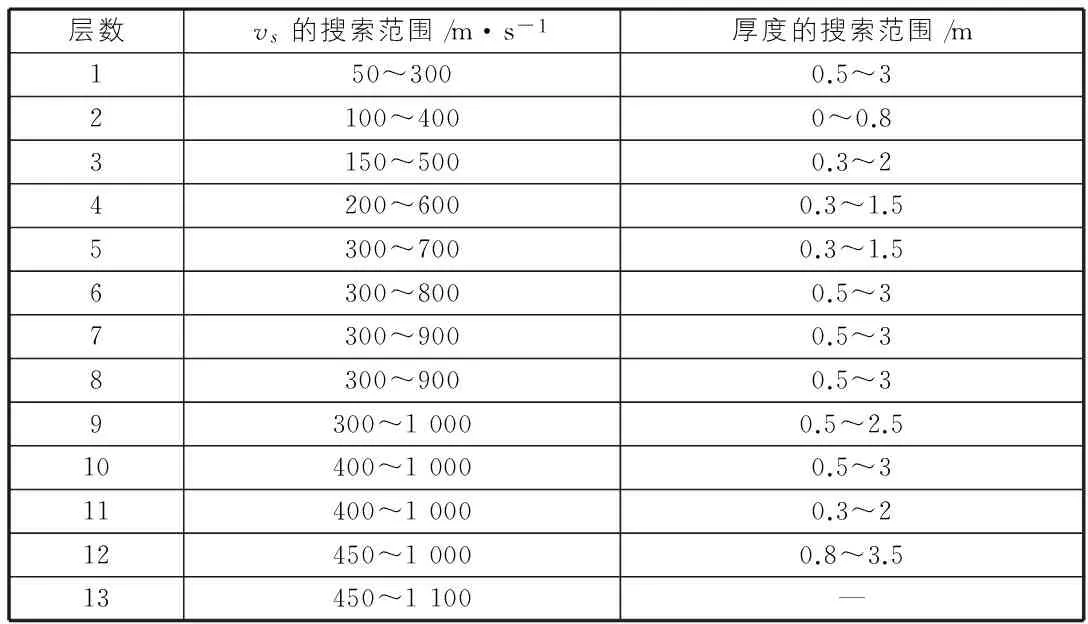
表2 反演参数搜索范围

为了检验改进遗传算法的合理性，我们利用标准遗传算法和改进遗传算法分别对反演计算。反演结果见表3。

表3 标准遗传算法、改进遗传算法的反演结果

由表3可以看出，总体上，改进遗传算法反演结果的相对误差均低于标准遗传算法。改进遗传算法反演结果优于标准遗传算法反演结果，反演得到各参数都较接近于真值，相对误差均低于1%。

根据反演结果得到频散曲线，见图4～图6。

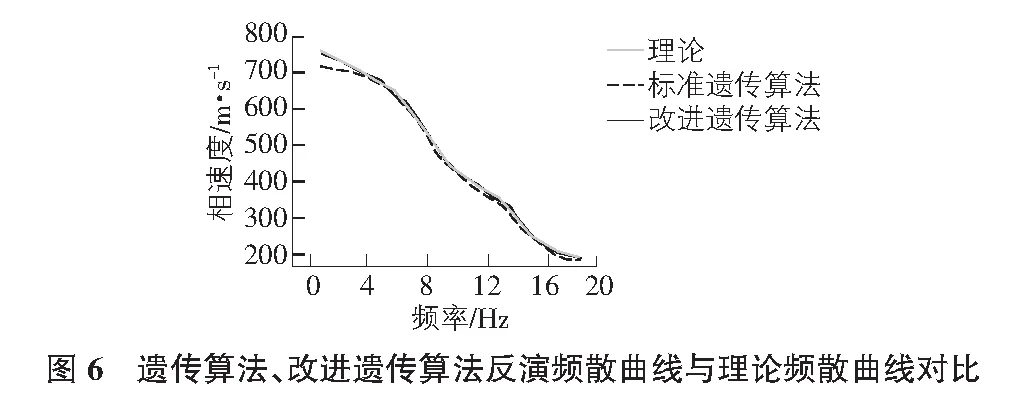
图4～图6是根据表3中标准遗传算法、改进遗传算法反演结果绘制出的频散曲线，并且与理论频散曲线展开对比的结果。从图4可看出，标准遗传算法反演频散曲线和理论频散曲线在4.8 Hz前存在较大差别，4.8 Hz以后吻合程度较好；从图5不难看出，改进遗传算法的反演频散曲线在这个过程中与理论频散曲线吻合相当高，两条线基本重合；再根据图6，可以清楚的看出改进遗传算法的反演频散曲线优越于标准遗传算法反演频散曲线，从而验证了遗传算法改进的实用性，为今后工程计算提供了依据。

4 结语

给出从青藏铁路北麓河段野外观测数据中提取频散曲线的处理方法，介绍了具有时频特征的小波分析提取相速度曲线，并验证小波分析法在提取相速度曲线的合理性。并根据提取的频散曲线，采用标准遗传算法和改进遗传算法分别反演频散曲线，经过与理论频散曲线对比，肯定了改进遗传算法的有效性，一方面提高了计算速度，另一方面提高了精度。

[1] 袁腊梅.层状介质中瑞利波频散方程及其线性研究[D].哈尔滨：哈尔滨工业大学，2008:2-5.

[2] 吴燕清,杨天春.瑞利波频散曲线的反演[J].煤炭学报,2008(10):1097-1101.

[3] 毛承英.基于改进遗传算法的瑞雷波频散曲线反演[D].长沙：中南大学,2010.

[4] 吴志坚，孙军杰，王兰民，等.青藏铁路沿线冻土场地地震动特征研究[J].岩石力学与工程学报，2007(12)：15-16.

[5] 崔建文.一种改进的全局优化算法及其在面波频散曲线反演中的应用[J].地球物理学报，2004，47(3):521-527.

Based improved genetic algorithm for inversion of Rayleigh waves dispersion curves

YIN Li JING Hai-he DONG Lian-cheng

(HeilongjiangUniversityofScienceandTechnology,Harbin150022,China)

Exploration medium parameters affect the dispersion curves were discussed, this paper presents an improved genetic algorithm inversion of Rayleigh wave dispersion curve problems. For the Qinghai-Tibet Railway Beiluhe venues inversion dispersion curves verify the validity of improved genetic algorithm. Experimental verification: use of improved genetic algorithm for Rayleigh wave dispersion curve inversion to improve the computing speed and accuracy.

medium, parameter, genetic algorithm

1009-6825(2014)15-0050-03

2014-03-14

尹 丽(1986- )，女，在读硕士； 景海河(1963- )，男，博士，教授； 董连成(1973- )，男，博士，副教授

TU195

A