基于模糊PI控制器的永磁同步电动机最大转矩电流比控制
2014-08-08舒佳驰刘明基郭韩金
舒佳驰, 刘明基, 郭韩金
(华北电力大学 电气与电子工程学院,北京 102206)
0 引 言
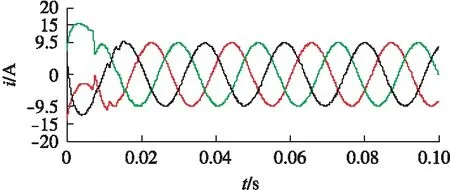
永磁同步电动机由于具有体积小、效率高、功率密度高等优点,使其实现的高性能驱动系统被广泛地应用于各种工业场合。对于内嵌式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM),其永磁体安装在转子铁心内,在结构上提高了电机的强度,为电机的高速运行提供了保障;由于永磁体的磁导率接近于空气,故电动机等效气隙不再是均匀的,d轴方向上的磁路磁阻要大于q轴方向上的磁阻,有Ld 对于永磁同步电机的各种控制方法,本质上在于通过对定子交、直轴电流的有效分配来实现对电磁转矩的控制。IPMSM近几年较为普遍的一种控制方法就是最大转矩电流比控制,对于该控制方法,许多文献都有相关的研究。通过理论推导计算,交、直轴电流与电磁转矩之间存在着复杂的函数关系,要准确实现最大转矩电流比(Maximum Torque Per Ampere, MTPA)控制比较困难。文献[2]通过离线计算、转矩给定并直接查表的方法来获得交轴电流,该方法需要占用大量的存储单元。文献[3]采用了近似线性函数的工程方法来处理交、直轴电流与转矩之间的关系,但需要合适的线性参数。文献[4]考虑了采用分段曲线拟合的方法,用多段二次曲线来逼近MTPA控制下的转矩与交、直轴电流关系曲线,该方法适合于高凸极率的永磁同步电机。本文推导了转矩电流比方程,根据极值原理计算得出该条件下的定子电流相位,推导得到交、直轴电流与转矩的关系,从而来实现调速系统下MTPA控制。 由于传统PI控制器的比例和积分系数不可调,系统在起动及变负载等情况下的动态性能不够好,响应时间长,超调及振荡大。为改善系统的动态性能,本文考虑转速环采用不依赖于被控对象数学模型的模糊PI控制器。该控制器可以实现参数的在线修正,提高了系统的动态性能,对外部干扰及电机参数的变化具有较强的鲁棒性能。 图1为两对极的IPMSM的截面图,永磁体在转子中为V字形布置,通过改变永磁体的位置和尺寸来调整电机交、直轴电感及电机特性。 图1 IPMSM的截面图 当忽略铁心的磁饱和、涡流及磁滞损耗等影响时,可以得到基于转子旋转d-q坐标系下的永磁同步电动机数学模型[1]。 电压方程: (1) 磁链方程: (2) 转矩方程: (3) 运动方程: (4) 式中:Ld、Lq——定子d、q轴电枢电感; rs——定子绕组电阻; ψf——转子永磁磁链; np——磁极极对数; ω——转子旋转电角速度; Tl——电机负载转矩; J——转动惯量; B——阻尼系数。 对于IPMSM,Te=f(id,iq),id=0的控制在输出相同电磁转矩时电机的定子电流不是最小的。采用MTPA控制,可以在输出相同转矩的情况下,充分利用磁阻转矩,最优分配交、直轴电流,获得最小定子电流,从而降低电机的电阻损耗,并降低对驱动器容量的要求。 基于转子旋转d-q坐标系下的定子电流矢量图如图2所示。 图2 基于转子旋转d-q坐标下定子电流矢量图 图2中β为定子电流与d轴夹角,可得: (5) 将式(5)代入式(3)中有转矩方程: (6) 则转矩电流比方程为 (7) 根据极值原理,要实现MTPA控制,即单位电流获得最大转矩的条件为 (8) 解式(8),所得β就为能够产生MTPA所需的电流相位: (9) 综合式(5)和式(9),可得 (10) 由于IPMSM有Ld (11) 考虑到id与转矩的关系式过于复杂,若已知iq,从式(10)中可以比较容易得到id。故本文在MTPA控制系统中,将式(10)、式(11)所得转矩电流关系作为电流调节器的交、直轴电流给定信号。MTPA控制的交直轴电流关系也可通过采用条件极值问题,构建拉格朗日函数进行求解得到[2]。图3为IPMSM的MTPA调速系统的框图。 图3 IPMSM的MTPA调速系统 传统PI控制器参数的确定,完全取决于被控对象的数学模型,而模糊控制系统的设计则不同,他并不依赖于被控对象的数学模型,主要是通过对多次积累的操作经验及大量的试验数据进行分析、归纳总结,得到适合系统输入输出的模糊关系。模糊控制器(Fuzzy Controller, FC)的设计过程主要包括: 确定模糊控制器的结构、设置输入输出变量及其隶属度、建立模糊规则、选定近似推理算法等[9]。 本文采用二维输入模糊控制器,他能更好地反映受控过程中输出变量的动态特性。FC以转速偏差e和偏差变化率ec作为输入量,在控制过程中不断对二者检测,根据二者变化值,结合模糊规则产生PI控制器中比例和积分系数的修正值,以对比例和积分系数在线调整。当给定量变化时,PI控制器中的kp、ki也随之改变。 图4 模糊PI控制器 模糊近似推理算法是一个量值模糊化、模糊量再清晰化的过程。根据输入量的物理论域设置e的模糊论域为[-1000,1000],其模糊子集为{负大,负中,负小,零,正小,正中,正大},记为{NB,NM,NS,ZE,PS,PM,PB},量化因子ke取为1。ec的模糊论域为[-1,1],模糊子集为{负大,负中,负小,零,正小,正中,正大},记为{NB,NM,NS,ZE,PS,PM,PB},量化因子kec取为1/100000。e和ec的隶属度函数如图5和图6所示。 图5 e隶属度函数 图6 ec隶属度函数 输入量e、ec经由模糊化后转化为模糊自变量,然后通过模糊推理得到模糊的因变量,经去模糊运算后,分别作为PI控制器的比例系数和积分系数的修正值Δkp和Δki输出。Δkp的模糊子集为{负大,负中,负小,零,正小,正中,正大},记为{NB,NM,NS,ZE,PS,PM,PB},其模糊论域为{-3,-2,-1,0,1,2,3}。Δki的模糊子集为{负大,负中,负小,零,正小,正中,正大},记为{NB,NM,NS,ZE,PS,PM,PB},其模糊论域为{-6,-4,-2,0,2,4,6}。 模糊控制规则是模糊推理的核心,也是修正PI系数的依据,其根据专家经验及理论分析建立。表1和表2为结合模糊控制规则,根据模糊输入量e和ec得到输出量Δkp和Δki的模糊值。 表1 Δ kp模糊控制规则 表2 Δ ki模糊控制规则 为验证所设计的MTPA控制系统的正确性,基于MATLAB/Simulink进行了仿真分析。电机参数如下: 定子电阻rs=2.875Ω,d轴电感Ld=4.5mH,q轴电感Lq=8.5mH,转动惯量J=8×10-4kg·m2,永磁体磁链ψf=0.175Wb,极对数np=4,阻尼系数B=0.001。分别搭建了id=0的控制系统及MTPA控制系统模型,其转速调节器分别采用传统PI和模糊PI控制器进行仿真分析。 图7中的角度β为电机带负载Tl=12N·m运行,给定转速为700r/min。IPMSM稳定运行时,满足产生MTPA条件的最佳定子电流相位。 图7 定子电流矢量与d轴夹角 对于IPMSM,由于Ld 图8 定子d轴电流 图9为在相同的电磁转矩下,id=0和MTPA控制时仿真所得的定子相电流波形。id=0控制所得相电流幅值约9.5A,而MTPA控制所得相电流幅值约8A。通过电流波形图比较可知: 在相同的电磁转矩给定时,MTPA控制下的定子电流比id=0控制时的要小。 图9 定子三相相电流 图10为永磁同步电机带负载Tl=12N·m运行,给定转速为700r/min时起动过程的局部放大图。 图10 起动过程的转速波形局部放大图 在仿真过程中,传统PI控制器的比例和积分系数固定不可调,导致了系统在接近给定转速时引起多次振荡和较大超调。模糊PI控制器,由于采用在线修正比例和积分系数的方法,能够实时地改变控制器的参数。虽然上升时间比之传统PI控制器稍长一些,但调节时间要远小于传统PI。当电机接近给定转速时,能有效减弱转速上升加速度,使电机更平稳地运行在给定状态。 图11验证了转速指令突变时传统PI和模糊PI控制器作用下,系统的突变响应能力。 图11 给定转速突变转速响应波形 当电机稳定运行在给定转速1000r/min,于0.03s时突降给定转速,采用传统PI控制器得到的转速响应经多次振荡才稳定,有较大的超调。采用模糊PI控制器得到的转速能够快速稳定地跟踪给定量,且超调非常小。从图11中也能够看到,这种调节优势在转速指令突变时更为明显。 本文对IPMSM调速的控制方法及策略进行了分析研究,在采用MTPA控制方法基础上对转速控制器进行了相应的改造设计。通过理论分析及仿真结果可得出: 相比于id=0控制,MTPA控制在相同的电磁转矩下,所需的定子电流更小;速度环所采用的模糊PI控制器,进一步提升了系统的动、稳态性能。仿真结果符合理论分析,证明了该系统较传统PI调速系统具有很大的优越性。 【参考文献】 [1] 袁登科,陶生桂.交流永磁电机变频调速系统[M].北京: 机械工业出版社,2011. [2] 黄鹏,黄雷,苗长云,等.考虑饱和效应的IPMSM最大转矩电流比控制[J].电力电子技术,2011,45(2): 41- 43. [3] 李长红,陈明俊,吴小役.PMSM调速系统中最大转矩电流比控制方法的研究[J].中国电机工程学报,2005,25(21): 169-174. [4] 李军,余家俊.基于分段曲线拟合的IPMSM最大转矩电流比控制研究[J].四川大学学报,2012,44(1): 307-311. [5] 尚重阳,邓利红,周建华,等.一种永磁同步电动机的最大转矩电流比控制方法[J].电气传动,2008,27(7): 90-92. [6] 姜禹强.基于DSP的交流伺服系统最大转矩电流比控制的研究[D].哈尔滨: 哈尔滨理工大学,2009. [7] 肖卫文,熊芝耀,李世春,等.基于变参数PI的永磁同步电动机矢量控制系统[J].电力电子技术,2009,43(4): 32-33. [8] 张伦健,陈利萍.基于智能PI的永磁同步电动机近似最大转矩电流比控制[J].微特电机,2012,40(8): 42- 45. [9] 张德丰.MATLAB模糊系统设计[M].北京: 国防工业出版社,2010. [10] 李庆春,沈德耀.一种新型的二维PID模糊控制器[J].控制工程,2011,18(4): 623-626.1 永磁同步电动机数学模型及MTPA控制
1.1 IPMSM模型结构

1.2 IPMSM的数学模型
1.3 MTPA控制算法

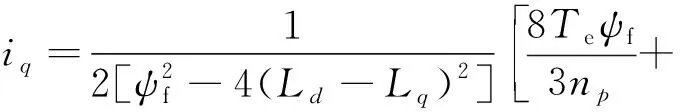

2 模糊PI控制器





3 控制系统的仿真及结果分析





4 结 语
