基于EM算法的光滑参数选择

吉 文 超

(重庆大学 数学与统计学院，重庆 401331)

1 概 述

(1)

2 光滑参数优化算法

2.1 REML方法

考虑到使用混合效应模型去估计光滑参数λ，下面将主要采用基于截断多项式样条基(TPFbases)的惩罚样条方法(penalizedspline)去估计光滑回归函数m(x)。从形式来讲，二者更容易建立联系。首先介绍p阶截断多项式样条基(truncatedpolynomialbasis)

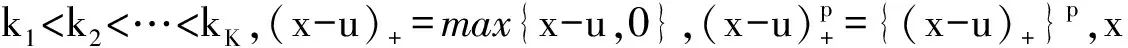
(2)

式(2)中，参数p，K分别表示样条基的阶数和节点个数，从其形式上可以直接观察到，系数参数βi，(i=0，1，…，p)和ui，(i=1，2，…，K)的估计值的优劣将直接影响样条模型对回归函数曲线的拟合。Wand(2003)和Ruppert，etal.(2003)建立了基于截断多项式基的惩罚样条模型与混合效应模型之间的联系，并且通过混合效应模型得到了样条基系数的最优线性无偏估计值(bestlinearunbiasedestimator)。

m(x)=Xβ+ZKu

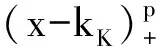
Vλ

(3)

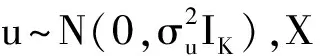
(4)

式(4)经过分解化简后可变形为

在得到光滑参数λ的估计值后，由此得到参数系数β，u的最优估计值，具体做法如下。

2.2 EM算法

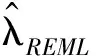
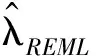
3 模 拟

考察3种光滑参数的选择方法，分别是GCV准则，REML准则和EM算法。将通过实验模拟更直观的展示不同选择方法的差异性，下面以模型残差作为主要分析对象去考察曲线拟合的优劣，采用RASE(rootaveragesquarederror)作为评价准则，即：

Cao(2010)曾用此准则评价基于样条方法的变系数模型函数系数拟合的优劣，为了消除随机性带来的影响，分别进行100次试验，并取其均值作为最终RASE值。

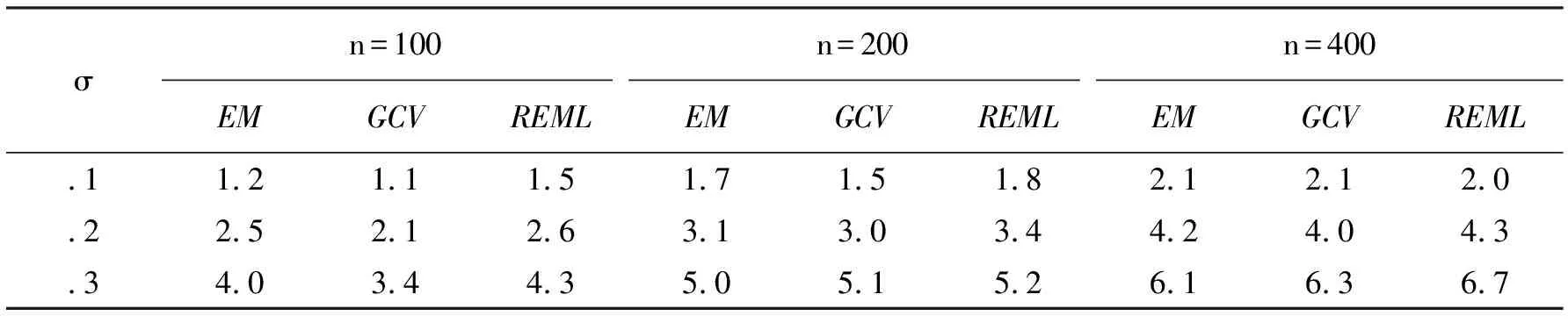
表1 3种不同光滑参数选择的对比

关于m1(x)的模拟分析，表中第一列和第一行分别对应的是噪音水平和样本容量。

首先选择目标函数，即：

m1=4.26(e-3.25x-4e-6.5x+3e-9.75x)

其对应的响应变量是y1=m1+ε1，ε1服从正态分布，x定义在区间[0，1]上。在函数模拟过程中，为了更客观地展示不同光滑参数选择准则的特点，采用3种不同大小的样本容量，分别为n=100，200，400和3种不同的方差大小σ=0.1，0.2，0.3，共计9组试验。在每一组试验中，分别求出基于3种不同光滑参数选择方法下的RASE值，并作对比(表1)，从表1中可以看出，基于GCV准则和REML准则的光滑参数选择差异不大，并且随着样本量的增加差异会逐渐减小，但是整体而言，基于REML准则的光滑参数选择下的模型误差要略大于前者，并且在相同样本容量下，这种差异并不会因为样本方差的弱化而减小，而EM算法能在一定程度上减小因REML准则欠光滑(undersmoothing)现象带来的模型误差。图1表示的是在方差σ=0.3的情况下，基于EM算法的模型拟合情况，黑色曲线表示测试函数m1(x)，另外3条拟合曲线分别表示在3种不同样本容量大小下的模型拟合情况。如图1所示，模型的拟合效果会随着样本量的增加而增加，特别当n=400时，蓝色曲线与黑色曲线高度重合。

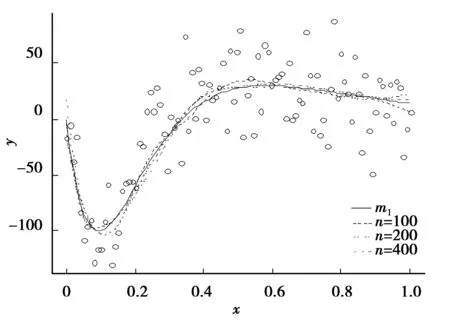
图1 目标函数m1(x)的散点图光滑

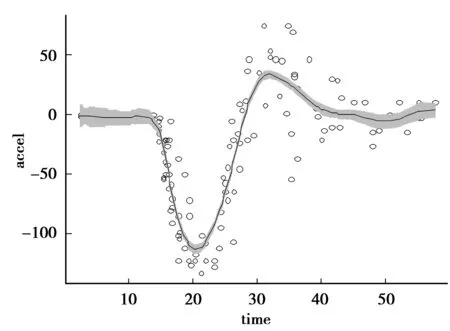
图2 关于motorcycle data的散点图光滑

4 实例分析

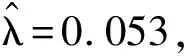
5 总 结

结合EM算法与REML方法来优化光滑参数，并与GCV方法和REML方法做了对比，结果显示在大样本情况下，EM算法能够提高模型的拟合精度，并在实例分析中取得了较好的拟合效果。但是对于非正态样本或者非独立方差情形下该算法的适应性和稳定性问题，仍需做更深入的研究。

参考文献：

[1] RUPPERT D，WAND M P，CARROLL R J. Semiparameteric Regression[M].Cambridge University： Cambridge university press， 2003

[2] SILVERMAN B W. Some Aspects of the Spline Smoothing Approach to Nonparametric Regression Curve Fitting[J].Journal of the Royal Statistical Society，1986，47：1-52

[3] KAUERMANN G. A Note on Smoothing Parameter Selection for Penalized Spline Smoothing[J]. Journal of statistical planning and inference ，2005，127：53-69

[4] WELHAM S J，CULLIS B R. A Comparison of Mixed Model Splines for Curve Fitting[J].Australian & New Zealand Journal of Statistics ，2007，49：1-23

[5] CAO Y，LIN H，WU T Z， et al. Penalized Spline Estimation for Functional Coefficient Regression Models[J].Computational statistics & data analysis，2010，54：891-905

[6] EILERS P H C，MARX B D. Flexible Smoothing with B-splines and Penalities[J]. Statistical science，1986(11)：89-121

[7] LEE T C M. Smoothing Parameter Selection for Smoothing Splines：a Simulation Study[J]. Computational Statistics & Data Analysis，2003，42：139-148

[8] GIJBEL S ，VERHASSELT A. P-splines Regression Smoothing and Difference Type of Penalty[J]. Stat Comput，2010，20：499-511