直推式支持向量机的研究学习
2014-08-08王利文刘琼荪
王利文, 刘琼荪
(重庆大学 数学与统计学院,重庆 401331)
支持向量机[1](Support Vector Machine,SVM)是目前机器学习中有效的学习机,在实际中取得了广泛的应用。但传统的支持向量机主要处理监督学习问题,即对未来所有样本的预期性能达到最优。而在实际学习中,往往只需要对一些特定的未知样本进行识别,于是考虑一种更为经济有效的分类器,使它能直接从已知样本对一些特定样本进行识别与分类。半监督支持向量机的学习方法能够将已标注的和未标注的样本所提供的聚类信息有机的结合,比传统分类算法更有助于解决实际问题,因此它正逐渐成为当前机器学习领域的研究热点。目前,半监督支持向量机算法主要有:Joachims提出的直推式支持向量机(TSVM)、Ting等提出的BoostSVM(boosting support machine),Belkin等人提出LapSVM算法。本文主要研究了直推式支持向量机学习算法。
1 直推式支持向量机
在传统的支持向量机学习方法中,学习算法的目标是使学习所得的分类器在训练集上有最小的错误率,用训练集的分布来近似预计测试集的分布。但在实际情况中,学习的目标是使训练得到的分类器在测试集上有尽可能小的实际误差。这也是直推式支持向量机所要解决的问题。目前,支持向量机的直推式学习算法的主要研究成果是T.Jocachims的直推式支持向量机(TSVM)[2]。下面简单介绍TSVM的算法原理和实现。

(1)
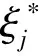
(1) 设置参数C和C*的初始值,使用归纳式学习对有标签样本进行一次初始学习,得到一个初始分类器,并按照某个规则指定一个无标签样本中的正样本标签样本数Np;
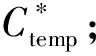
(3) 对所有样本进行重新训练,对新得到的分类器,按一定的规则交换一对标签值不同的测试样本的标签符号,使得模型(1)中的目标函数值获得最大的下降,复次循环,直到找不出符合交换条件的样本对为止;

2 直推式支持向量机的几种改进算法
2.1 渐近直推式支持向量机学习算法
TSVM算法将把无标签样本隐含的分布信息引入了支持向量机的学习过程中,比单纯地使用有标签样本训练得到的分类器在性能上有显著地提高。但该算法仍存在一些不足,主要缺陷是算法执行之前必须人为地指定待训练的无标签样本中的正样本数Np,而在实际上,Np的值很难较为准确地估计。在TSVM算法中,一般采用了一种简单的方法去估计Np,即依据有标签样本中的正标签样本所占的比例来近似地估计无标签样本集中的正标签样本的比例,从而估计出Np。但该方法在有标签样本数较少的情况下很容易导致较大的估计误差,当预先设定Np的值与实际的正标签样本数相差较大时,就会导致学习机性能的迅速下降。
陈毅松[3]等针对TSVM的上述缺陷提出了一种渐进直推式支持向量机(progressive transductive support vector machine,简称PTSVM)。在PTSVM算法[3]中,训练开始前,对无标签样本的分布特征不作任何估计,而在训练过程中选择对后续训练产生较大影响的无标签样本赋予当前状态下的标签值,并把它们加入到有标签样本集合中,然后进行新一轮的训练。为使获得更准确的分类超平面,该算法采用成对标注法和标签重置法来不断调整标签值。文献[3]中证明了成对标注法和标签重置法的合理性。PTSVM训练算法的具体步骤:
(1) 设置参数C与C*的初始值,对有标签样本使用归纳式学习进行一次初始学习,从而得到初始分类器;
(2) 使用初始分类器对无标签样本学习,计算每一个无标签样本的判别函数输出,用成对标注法则对当前边界区域内的无标签样本标注一个新的正、负样本标签;
(3) 重新训练所有样本,并计算每一个无标签样本的判别函数输出。若发现早期标注的某个无标签样本的标签值与当前的判别函数输出值不一致,则按照标签重置法取消对该样本的标注;
(4) 用成对标注法寻找当前边界区域内符合新加标注条件的未标注的无标签样本。若存在这样的无标签样本,则对其标注并返回(3);若不存在这样的无标签样本点,则用当前的分割平面对剩下的无标签样本做分类并加注标签。算法结束,并输出结果。
薛贞霞等在文献[4]中基于SVDD(支持向量域描述)的可信度设计提出了PTSVM的改进算法RPTSVM算法。首先对当前正类、负类有标签样本分别进行数据域描述,得到包含该类数据的最小半径的超球,再根据当前分类间隔区域内的无标签样本点与超球球心的距离设计无标签样本的可信度。根据事先设定的可信度阈值,对那些大于阈值的样本加以标注,这是一种区域标注法。显然,算法继承了PTSVM的渐进赋值和动态调整规则的优点,同时算法在稳定性及训练速度上得到了加强,使得算法能够更好的适应各种不同分布的训练样本。
2.2 TSVM中Np的确定新方法
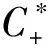
(2)
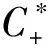
(3)
Np与Nn分别表示正负样本的数目,a为正常数。
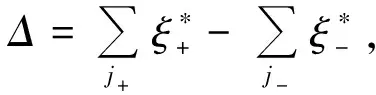
(4)
或者测试样本被标记为负样本,它所对应的松弛变量ξ*满足如下条件:
(5)
那么交换这个测试样本的标签,目标函数值会减少[5]。
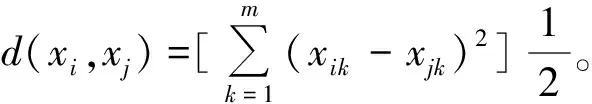
2.3 TSVM的模糊渐进式学习算法
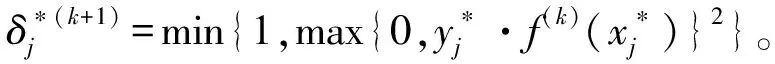


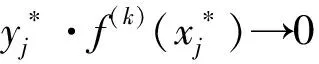
模糊隶属度的确定是一种动态的方式,它随着决策函数f(k)(·)的变化而不断地变化。因此,称该方法为模糊隶属度的“自适应”方法。
同时,在PTSVM算法中,“半标记”集合D始终是不断增加的,一方面把未标记样本集中的支持向量逐步引入D中,另一方面也把未标记样本集中的非支持向量引入D中。当TSVM的决策超平面趋于稳定时,半标定样本集中位于分类间隔边界之外的样本成为非支持向量的概率非常大,它们对TSVM的决策超平面没有什么帮助并且会增大计算和存储开销。FPTSVM算法将对这部分样本在半标记样本中删除,从而对混合训练集进行缩减,从而减轻了算法每个迭代步的计算开销。
2.4 最小二乘支持向量机的半监督学习方法(SLS-SVM)
不论是TSVM算法还是PTSVM算法过程都需要求解二次规划获得最优分类面。如果遇到大规模数据样本集时,训练效率极低。文献[9]在PTSVM算法的基础上提出了基于半监督学习的LS-SVM(最小二乘支持向量机)学习算法,记为SLS-SVM算法。LS-SVM中用二次损失函数来取代TSVM中的ε不敏感函数,从而将TSVM的二次规划问题转换为求解线性方程组的问题。在对无标签样本的处理方面,SLS-SVM采用的是区域标注法及标签重置法,使得算法具有一定的自适应差错修复能力。
2.5 实时数据更新的改进直推式支持向量机算法
当处理诸如网络入侵问题时,需要实时对数据进行分类,利用PTSVM时,在每次的渐进赋值和动态调整后都需要重新训练求解二次规划,训练效率就显得较为低下。文献[11,12]针对入侵数据集的数据样本,从两个方面优化了PTSVM算法。一是采用一种有倾向的区域标注方法;二是采用增量与减量算法。当标注一个无标签样本点后,采用增量迭代更新算法;当修改早期标注错误的无标签样本点时,则采用减量方法。这将克服每次渐进赋值和动态调整后所需要重新训练的缺陷。区域标注法的思想:
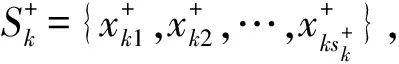
s.t. 0 (6) 由式(6)描述区域内的样本标为负标签,假设符合条件的无标签样本数为m。 s.t. -1 (7) 其中 (8) 在TSVM与未经改良的PTSVM算法中,当发现早期标注的样本点与当前判别函数输出不一致时,需要重新训练,频繁求解优化模型。改良的PTSVM会取消上述不一致的标签,按照减量方法更新非支持向量集合和α,b,f(x),训练时间上会大幅减少,明显提高训练的效率。 如果训练样本集数目不足、分类的双方存在着数据不平衡的情况,文献[13]提出了一种新的基于TSVM的半监督分类算法(Semi SVM)。该算法通过对半标定样本的选择和惩罚参数C*的调节来实现。 (1) 半标定样本点的选择。在选择半标定样本加入到混合训练样本集的时候,主要考虑两点:选择的样本应该被加入到正确的类别中;应该选择含有“信息”的半标定样本。因为分类超平面是建立在支持向量的基础之上,所以应该选择含分类信息最丰富的两类样本的支持向量。 ψmax=max(ψ+,ψ-),ψmin=min(ψ+,ψ-) 设Amax为ψmax中样本的个数,Amin为ψmin中样本个数。为了处理不平衡数据,针对两类数据分别定义了不同的的阈值公式: (9) (10) 当候选集中的样本的|f(x)|值大于阈值时,该样本被加入到混合样本集中,成为半标定样本,并将这些样本从候选样本集中除去,以更新候选集和混合样本。 (11) 以此求得每次迭代决策函数中的半标定样本的惩罚参数。这样在迭代运算过程中,使得C*的改变与半标定样本的选择结合到一起,并处于动态的调节中的。该算法的具体步骤可参考文献[13]。 文献[16]运用上述算法,它不是将分类间隔内所有的样本加入到候选集中,而是只将那些判别函数的绝对值大于或者等于事先设定的阈值的样本加入候选集中。而且为了平衡样本,取N=min(N+,N-),这样加入候选集中相同数目的正负样本,有效避免了因样本分布不均衡导致分类超平面的偏移。 上述算法能够得到更为可靠的分类效果,但当训练样本数目较多时上述迭代过程的训练工作量也较大,且迭代次数T的确定问题也需要进一步的研究。 本文基于支持向量机分类的固有特点,阐述了直推式学习思想,介绍了几种改进直推式学习算法的支持向量机分类算法。这些分类算法无论是利用成对标注法还是区域标注法都能有效地对无标签样本点循序渐进地作出判别分类,并利用动态调整的规则使分类器具有一定的差错修复能力,在保证算法精度的同时提高了训练的速度。支持向量机作为机器学习的一个重要内容,涉及众多的学习领域,例如人脸识别与检测、图像分类、文本分类、医疗诊断等。直推式学习是一个较新的研究领域,很多方面尚不成熟、不完善,许多的研究工作还仅处于初步阶段。本文针对直推式支持向量机的学习算法做了一些总结研究工作,但在一定程度上还有很多有意义的课题值得进一步的挖掘和研究。 参考文献: [1] VAPNIK V.Statistical Learning Theory[M].New York,USA:Wiley Press,1998 [2] JOACHIMS T.Transductive inference for text classification using support vector machines. In:Proceedings of the 16thInternational Conference on Machine Learning[J]. San Francisco:Morgan Kaufmann Pulishers,1999.200-209 [3] 陈毅松,汪国平,董士海.基于支持向量机的渐近直推式分类学习算法[J].软件学报,2003,14(3):451-460 [4] 薛贞霞,刘三阳,刘万里.基于SVDD的渐近直推式支持向量机学习算法[J].模式识别与人工智能.2008,21(6):721-727 [5] WAHG Y. Training TSVM with The Proper Number of Positive Samples[J].Pattern Recognition Letters 26,2005:2187-2194 [6] 丁要军,蔡皖东.采用两阶段策略模型的P2P流量识别方法[J].西安交通大学学报.2012,46(2):45-50 [7] YU X,YANG J,ZHANG J P. A Transductive Support Vector MachineAlgorithm Based on Spectral[J].AASRI Procedia.2012,1:384-388 [8] 王磊.支持向量机学习算法的若干问题的研究[C].电子科技大学博士论文,2010:97-105 [9] ZHANG R,WANG W J,MA Y C. Least Square Transduction Support Vector Machine[J]. Neural Process Lett,2009(29):133-142 [10] 赵莹.半监督支持向量机学习算法研究[C].哈尔滨工程大学博士论文,2010:38-45 [11] 刘宇,朱随江,刘宝旭.采用改进PTSVM的入侵检测研究[J].计算机工程与应用,2012,48(5):1-4 [12] CHEN M S,HO T Y,HUANG D Y.Online Transductive Support Vector Machines for Classification[J].2012IEEE.2012:258-261 [13] 王安娜,李云路.一种新的半监督直推式支持向量机分类算法[J].仪器仪表学报,2011,32(7):1546-1550 [14] MAULIK U,MUKHOPADHYAY A.Gene-Expression-Based Cancer Subtypes Predition Through Feature Selection and Transductive SVM[J].IEEE TRANSACTIONS ON BIOMEDICAL ENGINEERING,2013,60(4):1111-1117 [15] DEBASIS C,SHIBU D.Cancer Classification through Feature Selection and Transductive SVM Using Gene Microarray Data.2012 Thid International Conference on Emerging Applications of Information Technology [J].IEEE.2012.77-80 [16] DEBASIS C,UJJWAL M.Semisupervised Pixel Classification of Remote Sensing Imagery Using Transductive SVM.2011 International Conference on Recent Trends in Information Systems[J].IEEE computer society,2011:30-35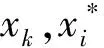
2.6 Semi TSVM 算法[13]

2.7 改进的TSVM最新算法
3 总 结
