关于不定方程x3±8=109y2

安 莹， 郭凤明

(西南大学 数学与统计学院，重庆 400715)

不定方程x3±8=Dy2(其中D是无平方因子的正整数)是一类基本而重要的不定方程，对它已有不少研究工作.1942年，Ljunggren[1]证明了当D不能被3或6k+1形的素因数整除时，方程最多只有一组正整数解.1981年，柯召、孙琦[2]进一步证明了如果D满足前述条件，并且如果D≡0，2，3(mod 4)时，方程x3+8=Dy2仅有整数解(x，y)=(-2，0)；如果D满足前述条件，并且如果D≡0，1，2(mod 4)时，方程x3-8=Dy2仅有整数解(x，y)=(2，0).1992年，曹玉书、黄龙铉[3]讨论了D含有6k+1形的素因数使x3±8=Dy2仅有平凡解的情况；1995年，罗明[4]证明了x3-8=7y2仅有整数解(x，y)=(2，0)；x3+8=7y2仅有整数解(x，y)=(-2，0)，(-1，±1)，(10，±12).此处在上述基础上利用同余式和递归数列方法讨论不定方程x3±8=109y2在gcd(x，y)=1时的整数解.

1 主要结果

定理1 不定方程

x3+8=109y2，x，y∈Z

(1)

无满足gcd(x，y)=1的整数解.

定理2 不定方程

x3-8=109y2，x，y∈Z

(2)

无满足gcd(x，y)=1的整数解.

2 证 明

2.1 定理1的证明

若x≡0(mod 2)，则由式(1)有y≡0(mod 4)，这与gcd(x，y)=1矛盾，故x≡1(mod 2).

现设x≡1(mod 2)，此时(x+2，x2-2x+4)=1或3，不定方程(1)给出下列4种可能的分解：

情形Ⅰx+2=109a2，x2-2x+4=b2，y=ab.

情形Ⅱx+2=a2，x2-2x+4=109b2，y=ab.

情形Ⅲx+2=327a2，x2-2x+4=3b2，y=3ab.

情形Ⅳx+2=3a2，x2-2x+4=327b2，y=3ab.

以下分别讨论这4种情况所给出的式(1)的整数解.

情形Ⅰ 解第2式得x=0，2，均不适合第1式.该情形无满足不定方程(1)的整数解.

情形Ⅱ 由假设x≡1(mod 2)，所以由第1式得x≡3(mod 4)，再由第2式得b2≡3(mod 4)，这不可能.故该情形也无满足不定方程(1)的整数解.

情形Ⅲ 将第2式化为(x-1)2+3=3b2，并将第1式代入得

b2-3(91a2-1)=1

(3)

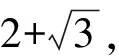
(4)

因此有

91a2-1=sn，n∈N

(5)

但容易知道a≡1(mod 2)，故只需考虑sn≡0(mod 2).

容易验证sn满足递归数列

sn+2=4sn+1-sn，s0=0，s1=1

(6)

可知当n≡1(mod 2)时，sn≡1(mod 2)，矛盾.故只考虑n≡0(mod 2)的情况.

对sn的递归关系(6)取mod 91，得到剩余类序列周期为24，有表1.

表1 sn(mod 91)的递归关系表

而由式(5)得sn≡90(mod 91)，矛盾.故该情形也无满足不定方程(1)的整数解.

情形Ⅳ 由假设x≡1(mod 2)，所以由第1式得x≡1(mod 8)，再由第2式得7b2≡3(mod 8)，这不可能.故该情形亦无满足不定方程(1)的整数解.

综上所述，可知不定方程x3+8=109y2，x，y∈Z，gcd(x，y)=1无整数解. 证毕.

2.2 定理2的证明

若x≡0(mod 2)，则由式(2)有y≡0(mod 4)，这与gcd(x，y)=1矛盾，故x≡1(mod 2).

现设x≡1(mod 2)，此时(x+2，x2-2x+4)=1或3，不定方程(2)给出下列4种可能的分解：

情形Ⅰx-2=109a2，x2+2x+4=b2，y=ab.

情形Ⅱx-2=a2，x2+2x+4=109b2，y=ab.

情形Ⅲx-2=327a2，x2+2x+4=3b2，y=3ab.

情形Ⅳx-2=3a2，x2+2x+4=327b2，y=3ab.

以下分别讨论这4种情况所给出的式(6)的整数解.

情形Ⅰ 解第2式得x=0，-2，均不适合第1式.该情形无不定方程(2)的解.

情形Ⅱ 由假设x≡1(mod 2)，所以由第1式得x≡3(mod 4)，再由第2式得b2≡3(mod 4)，这不可能.故该情形也无满足不定方程(2)的整数解.

情形Ⅲ 由假设x≡1(mod 2)，所以由第1式得x≡1(mod 8)，再由第2式得b2≡5(mod 8)，这不可能.故该情形亦无满足不定方程(2)的整数解.

情形Ⅳ 将第2式化为(x+1)2+3=327b2，并将第1式代入得

109b2-3(a2+1)=1

(7)

由引理1知方程(7)的全部整数解由式(8)给出

(8)

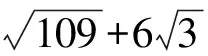
综上所述，不定方程x3-8=109y2，x，y∈Z，gcd(x，y)=1无整数解. 证毕.

参考文献：

[1] LJUNGGREN W. Satze Uber Unbestimmte Gleichungen[J]. Skr Norske Vid Akad Oslo，1942(9)：53-55

[2] 柯召，孙琦.关于不定方程x3±8=Dy2和x3±8=3Dy2[J].四川大学学报：自然科学版，1981，18(4)：1-5

[3] 曹玉书，黄龙铉.关于丢番图方程x3±8=Dy2[J].黑龙江大学学报：自然科学版，1992，9(2)：1-5

[4] 罗明.关于不定方程x3±8=Dy2[J].重庆师范学院学报：自然科学版，1995，12(3)：29-31

[5] WALKKER D T. On the Diophantine EquationmX2-nY2=±1[J].Amer Math Monthly，1967(74)：508-510