拓扑空间中ω-极限集的几个性质*
2014-08-08金渝光
谢 洁, 金渝光
(重庆师范大学 数学学院,重庆 401331)
ω-极限点的概念是由周期点的概念推广而得到的,是动力系统中的重要概念.在区间自映射的ω-极限集的研究,以及圆周自映射ω-极限集的研究中已经对度量空间中ω-极限集的一些性质进行了详细的证明.此处通过对一般拓扑空间中闭集的研究,并且运用数学分析中的一些知识得到了拓扑空间上ω-极限集的一个性质,也就是定理1中得到的结果.对于拓扑空间加以一定的条件,可以得到轨道orbf(x)为非空有界闭的连通集,也就是定理2的结果.通过对度量空间中ω-极限集的研究可以得到拓扑空间中ω-极限集的一个性质,定理3给出了证明.
1 预备知识
定义1[1]设X为拓扑空间,G为时间拓扑半群,如果F:X×G→X连续且满足对任意x∈X,以及任意t,s∈G,有
(1)F(x,0)=x.
(2)F(x,t+s)=F(F(x,t),s).
则称F为X上的拓扑动力系统.
定义2[2]设(X,f),(Y,g)都是动力系统,如果存在同胚h:X→Y使得对任何x∈X,h∘f=g∘h,则称f与g拓扑共轭;若f,g都是满射,h为连续满射,则称f与g拓扑半共轭.
定义3[3]y∈X为x的ω-极限点,如果存在正整数的子序列{ni},使当ni→∞,fni(x)→y,x的所有ω-极限点的集合叫做x的ω-极限集,记做ω(x,f).

定理1[5]设X为拓扑空间,则下列条件等价:
1)X不连通.
2) 存在X中两个非空闭集A,B使X=A∪B,A∩B=∅.
证明
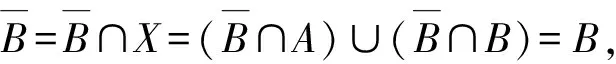
定理2[6]闭包是包含这个集合的最小闭集.
证明见参考文献[7].
定理3[7]ω(x,f)是X的闭子集.
证明

命题1 设ni为正整数的子序列,则对任何n>0,存在r,0≤r 证明 对每个ni,存在整数pi≥0以及0≤ri 命题2 设A是拓扑空间X中的点集,x∈X,那么下列事件等价. 2)x的每个领域o(x)中有A的点. 3) 有点列xn⊂A,使得∀o(x),有N,当n>N时,xn∈o(x). 证明 命题3 在拓扑空间中x的点集A为闭集⟺A中任何收敛点列极限属于A. 证明 充分性.对任意x∈d(A),由命题2,存在{xn}⊂A,xn≠x,xn→x(n→∞),而x∈A,所以d(A)⊂A,A为闭集. 定理4 设X为序列紧致的T2空间,Y为拓扑空间,f:X→X,g:Y→Y均为连续映射,h:X→Y是介于f与g之间的拓扑半共轭,则对任意y∈Y,任意x∈h-1(y),有h(ω(x,f))=ω(y,g). 证明 对∀t∈h(ω(x,f)),∃z∈ω(x,f),使得h(z)=t,因z∈ω(x,f),则存在正整数序列ni→+∞(i→+∞),使得fni(x)→z,又因为h为拓扑半共轭,有h∘fni(x)=gni∘h(x)=gni(y)→h(z)(i→+∞),t∈ω(y,g),所以h(ω(x,f))⊂ω(y,g). 反过来,若有t∈ω(y,g),则存在正整数序列ni→+∞,使得gni(y)→t,有h∘fni(x)→t.因为X为序列紧致的T2空间,{fni(x)}有收敛子序列{fnij(x)}收敛到X中的点u,由命题3知u∈ω(x,f),h∘fnij(x)=gnij(y)→h(u),由极限的唯一性知t=h(u),ω(y,g)∈h(ω(x,f)),综上所述,有h(ω(x,f))=ω(y,g). 定理5 设X是一个可度量化的拓扑空间,设其度量为d,若f:X→X是一个连续映射,则轨道orbf(x)的ω-极限集为非空有界闭的连通集. 证明 定理6 设f为拓扑空间(X,τ)上的连续映射,设n>0,则x∈ω(x,f)当且仅当x∈ω(x,fn). 证明 充分性.设x∈ω(x,fn),则存在ni→∞使得(fn)ni(x)→x,即fn+ni(x)→x,则x∈ω(x,f). (1)Un-1⊂Un-2⊂…⊂U0. (2)fmjk(Uk)⊂Uk-1,k=1,2,…,n-1. (3)fmjk(x)∈Uk-1,k=1,2,…,n. 于是有fmj1+mj2+…+mjn(x)∈U0,又因为mj1+mj2+…+mjn=0,所以x∈ω(x,fn). 参考文献: [1] 廖公夫,王立冬,范钦杰.映射迭代与混沌动力系统[M].北京:科学出版社,2013 [2] 张景中,熊金城.函数迭代与一维动力系统[M].成都:四川教育出版社,1992 [3] 陈二才.圆周自映射的ω-极限集[J].南京师范大学学报:自然科学版,1990,13(4):7-14 [4] 杨润生.无马蹄的圆周自映射[J].南京师范大学学报:自然科学版,1989,12(1):26-41 [5] 林银河.拓扑空间中序列的聚点集与轨道的ω-极限集[J].长春师范学院学报:自然科学版,2006,25(2):16-17 [6] 邢志涛,傅本路.关于ω-极限集的一点注记[J].肇庆学院学报,2006,27(2):8-21 [7] 熊金诚.点集拓扑讲义[M].北京:高等教育出版社,2003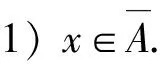



2 主要结论