基于MESH技术的伴随权重窗自动生成方法及其应用
2014-08-08邱有恒李百文赵英奎
邱有恒,邓 力,李百文,赵英奎
(北京应用物理与计算数学研究所 计算物理实验室,北京 100094)
对于大型复杂系统或深穿透问题,直接蒙特卡罗方法的计算效率很低。通过设置合理的重要性函数,用于指导粒子的赌与分裂,使重要的粒子多抽样,不重要的粒子少抽样,可大幅提升计算效率[1-2]。
重要性函数反映从相空间(包括几何空间、能量、时间等)发射的粒子的相对重要性,其实质是偏倚函数。显然,理想的重要性函数值应是正比于该相空间内的粒子对探测器的贡献。但在获得精确的数值模拟结果前,各相空间的重要性函数值未知,可通过多次迭代逐步逼近获得理想的重要性函数和精确数值模拟结果[3-4]。
几何重要性函数和权重窗技巧[5]是两种常用的重要性函数。与几何重要性函数相比,权重窗技巧的本领更强,它能反映不同几何空间、能量间隔、时间间隔的粒子的重要性,既能作用于栅元界面,也能作用于碰撞点。且MCNP程序有权重窗发生器功能,可多次迭代自动产生优化的权重窗参数。因此,在解决大型复杂系统或深穿透问题中,权重窗技术较几何重要性函数更灵活、方便,效果更好。
MCNP程序有两种权重窗发生器,一种是正算权重窗发生器,另一种是多群伴随权重窗发生器。目前,MCNP程序只能提供基于栅元的伴随权重窗发生器。对一些含重复结构或非对称结构栅元的模型,由于MCNP程序不能自动计算他们的体积,伴随权重窗发生器将失效。
本文借鉴MCNP程序正算MESH权重窗发生功能[6],对多群伴随权重窗发生器进行基于MESH技术的伴随权重窗自动产生功能,并应用于光子散射基准模型模拟。
1 权重窗技术
权重窗是诸多降低方差技巧中的一种[4]。权重窗有权重窗下限WL、权重窗上限WU、存活粒子权重WS3个参数。若粒子权重低于WL,将对粒子实施轮盘赌游戏;若粒子权重高于上限WU,将对粒子实施分裂游戏;其他情况不做处理。权重窗对不重要的粒子少花计算资源,节省计算时间;对重要粒子多花计算资源,从而降低计算方差,并最终提高计算效率。
2 伴随权重窗自动产生方法
2.1 伴随通量作为重要性函数的理论基础
蒙特卡罗方法求解粒子输运方程通常是解发射密度型积分方程[2]:

(1)
其中:ω(s)为发射密度;K(s′→s)为转移函数;Q(s)为源。各种响应量I(反应率、剂量率等)均可通过响应函数g(s)与发射密度的卷积实现,有:
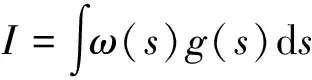
(2)
与之对应的伴随输运方程为:
(3)
K+(s′→s)=K(s→s′)
(4)
将式(1)乘以ω+(s),式(3)乘以ω(s),相减后积分,可得:
(5)
可见,伴随发射密度ω+(s)的意义是1个源粒子对I的贡献,也可称为价值函数。
伴随通量与伴随发射密度的关系为:
(6)
其中:T(r′→r|Ω,E)为输运核;Σt(r,E)为总截面。因此,伴随通量是天然的重要性函数。
2.2 从伴随通量产生权重窗的方法
由于不同栅元、不同能群的伴随通量可能有量级的差别,若直接使用伴随通量指导粒子输运可能造成粒子径迹或权重的大幅波动。因此,需对伴随通量进行处理以避免大幅波动。首先,对伴随通量进行一系列平滑处理,使相邻相空间伴随通量之比不过大。然后,根据相应的参数产生权重窗下限系数,基本思想是权重窗下限反比于伴随通量。假定参考栅元中最大的伴随群通量为e,用户指定的参考栅元权重窗下限参数为fnw(默认为1),平滑指数为pm(0~1),按式(7)产生栅元i、能群g对应的权重窗下限参数。
(7)
参考栅元一般为正算的源栅元,若fnw取默认值1,源栅元的权重窗下限均≥1,即源粒子均将进行轮盘赌,存活下来的粒子权重上升,可游动到更远的地方。
2.3 基于MESH技术的伴随权重窗实现方法
利用MCNP程序的FMESH功能可得到基于虚拟网格技术的伴随通量分布,由此可避开重复结构或其他非对称结构不能计算体积的难点。MESH网格是圆柱体或长方体,每个小的虚拟网格为规则的几何体,便于计算体积。对每个小的虚拟网格,采用径迹长度估计方法计算体通量。
在模块fmesh_mod中增加一子程序amesh,在amesh中对各相空间伴随通量进行平滑等处理,产生最终的权重窗下限,并按正算mesh-based权重窗发生器的格式输出在wwout文件中。程序经修改后,在输入卡片inp中只要同时有正算的mesh权重窗发生器参数和fmesh计数,并采用多群伴随输运模式,即可产生mesh-based伴随权重窗。相关的子程序调用情况大致如下:
1) 子程序avrwgi输出mesh权重窗定义参数,如能群、网格划分等,由于输入卡片中有正算mesh权重窗产生指令,这一步会正常进行;
2) 在子程序summary中,先调用子程序fmesh_print输出fmesh计数结果,然后调用权重窗输出子程序avrout;
3) 在avrout中,若满足既有mesh权重窗,又是伴随输运,则调用amesh产生伴随mesh权重窗系数;
4) 在amesh中,利用fmesh的多维通量记录数组完成伴随通量平滑并产生最终权重窗系数。
3 数值算例
3.1 重复结构模型验证
图1为MCNP程序中自带的一重复结构例题,大致结构为半径15 cm的球,上、下半球分别被两种格子模型填充,1号栅元内各向同性发射均匀球体积源,测点在上半球。
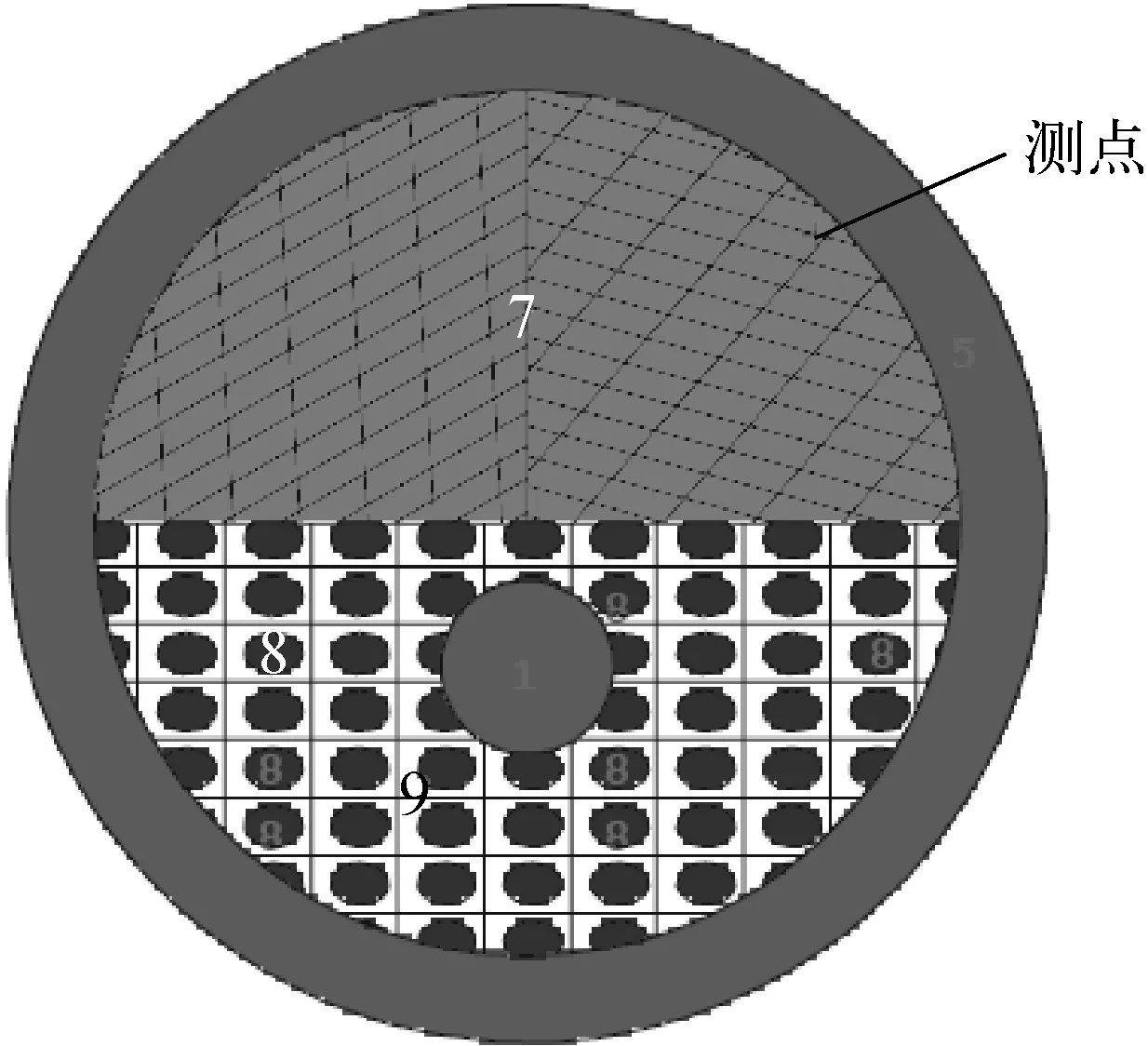
图1 重复结构模型
若采用几何重要性函数(imp卡片),则下半球中所有的8号小球区具有相同的重要性,所有的9号栅元(空白区)具有相同重要性,上半球中左侧所有7号格具有相同重要性,右侧所有7号格具有相同重要性,这显然是粗糙甚至不合理的重要性函数设置。为便于比较,将各栅元几何重要性全设置为1,即等价于无重要性函数。
若采用MCNP程序基于栅元的多群伴随输运权重窗功能(cell-based),则由于不能计算体积无法开展计算。由注量率和计算效率的比较(表1)可知,采用mesh-based伴随权重窗后,计算结果几乎不变,统计误差更小。为便于比较,常用优度FOM[4]反映计算效率,FOM越大,计算效率越高。采用伴随权重窗后的FOM约为无重要性函数的8.77倍。
图2为其中1个能群(0.82~1.35 MeV)的伴随权重窗下限分布云图。权重窗下限系数反比于重要性,从图2可见,测点附近区域的重要性最高(权重窗下限最低,分裂概率最大),距测点越远重要性越低,4个角上的深色区域为超出模型的部分,重要性为0,权重窗下限也为0。

表1 注量率和优度的比较

图2 能群z=0平面伴随权重窗下限分布云图
3.2 光子空气散射基准问题
为检验数值模拟程序和参数精度,美国堪萨斯州立大学于1977年开展了光子在空气中散射的基准实验[7],实验采用60Co点源,位于水泥柱壳的对称轴上高出地面198.12 cm处,从源出发的光子被水泥柱壳校准成150.5°方向上的一圆锥束,水泥柱壳足够厚以至于穿出柱壳的光子可忽略不计(图3)。探测器分别放在水泥柱壳一侧的50、100、200、300、400、500、600、700 m远离地面上方1 m处。文献[7-8]分别采用不同版本MCNP程序模拟了该问题,文献[7]模拟结果与实验结果符合较好,但未公布FOM。文献[8]采用并行化的MCNP4C版本,样本数为1亿,模拟结果与实验结果相差较远,具体原因未知。为提高计算效率,本文考虑人为设定几何重要性,最大达400(图4)。

图3 水泥柱壳剖面图

图4 几何重要性设置
本文取最难计算点(700 m,0 m,1 m)作为对比计算模型,首先以此点作为伴随输运的源点,并采用角度偏倚抽样方案,获得MESH格式下各相空间伴随通量,据此生成权重窗下限系数,图5示出了其中较重要能群(0.8~1 MeV)在z=1 m这层几何上权重窗下限系数分布,其中,源点是正算的源点和伴随计算的参考点,探测器是伴随的源点和正算的测点。可见,距离探测器越近的空间,权重窗下限系数越低,即这些区域更重要。
本文采用MCNP5程序在计算机上分别开展无重要性的直接模拟和采用伴随权重窗技巧模拟。采用直接模拟,即便样本数达107,MCNP程序规定的10项统计指标有error、vov、slope 3项未达要求,计算结果和统计误差与文献[8]相当(表2),但FOM大很多,这可能与程序版本有关。
采用伴随权重窗技巧模拟时,样本数仅5×106,10项统计指标全部通过,说明收敛正常,结果可信度高,伴随权重窗结果与实验吻合很好(已将文献[7]中照射率单位转换为国际单位,从通量到照射率的转换公式可参考文献[7]),相对偏差仅1.2%。采用伴随权重窗的FOM约为直接模拟的8倍,计算精度和效率均高于文献[8]。

图5 能群z=1 m平面伴随权重窗下限分布云图

表2 本文与文献的照射率和优度比较
4 结论
本文在MCNP程序上实现了基于MESH技术的伴随权重窗自动产生功能,弥补了MCNP程序多群伴随权重窗发生器不能用于含重复结构等复杂几何模型的缺陷。将基于MESH技术的伴随权重窗技巧应用于光子散射基准实验模拟,计算结果与实验值吻合很好,相对偏差仅1.2%,计算效率约为直接模拟的8倍。
参考文献:
[1] 谢仲生,邓力. 中子输运理论数值计算方法[M]. 西安:西北工业大学出版社,2005.
[2] 杜书华,等. 输运问题的计算机模拟[M]. 长沙:湖南科学技术出版社,1988.
[3] MENDIUS P W. Group IS-11, MCNP: Multigroup/adjoint capabilities, LA-12704[R]. USA: Los Alamos National Laboratory, 1994.
[4] BRIESMEISTER J F. MCNP: A general Monte Carlo code forN-particle transport, LA-12625-M[R]. USA: Los Alamos National Laboratory, 2000.
[5] HENDRICKS J S, CULBERTSON C N. An assessment of MCNP weight windows, LA-UR-00-55[R]. USA: Los Alamos National Laboratory, 2000.
[6] LIU L R, GARDNER P. A geometry-indepen-dent fine-mesh-based Monte Carlo importance generator[J]. Nucl Sci Eng, 1997, 125(2): 188-195.
[7] OLSHER R H, HSU H H, HARVEY W F. Benchmarking the MCNP Monte Carlo code with a photon skyshine experiment[J]. Nucl Sci Eng, 1993, 114(3): 219-227.
[8] 潘流俊,邓力. 光子散射基准问题的Monte Carlo模拟[J]. 清华大学学报:自然科学版,2007, 47(增刊):955-959.
PAN Liujun, DENG Li. Monte Carlo simulations of the photon skyshine benchmark problem[J]. J Tsinghua Univ: Sci & Tech, 2007, 47(Suppl.): 955-959(in Chinese).
