垂直下降液膜波动特性实验研究与谱分析
2014-08-08臧丽叶田瑞峰刘晓一孙兰昕
臧丽叶,田瑞峰,刘晓一,孙兰昕
(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001; 2.深圳中广核工程设计有限公司 上海分公司,上海 200241;3.渤海船舶重工有限责任公司,辽宁 葫芦岛 125004)
自由降液膜的流动展示了非常丰富且复杂的波动力学特性,其波动的时空演化具有强烈的非线性特性,除此之外,Re的差异又使液膜的波动状态呈现多样性特征[1-3]。液膜波动特性会影响到液膜的流动稳定性,并改变其传热特性,例如当液膜波动剧烈以致破断时会造成热壁局部干涸,使传热恶化。因此,液膜波动特性对于控制液膜厚度、强化薄膜传热、预测与防止液膜破断等实际工程应用有重要意义。而对液膜厚度的统计分析是研究液膜波动特性的主要途径之一。但由于液膜厚度很薄,且流动速度相对较快,因此如何准确捕获实时液膜厚度成为研究液膜特性的关键[3]。
国内外有很多研究者对液膜的波动特性展开了研究,大多关注液膜厚度的时序变化特性,忽略其频域特性[4-6]。而由于液膜厚度变化并非简单的简谐振动,时间域的描述往往不易全面地、深刻地反应其动态特性。例如,此液膜波动信号含有哪些频率成分、何种频率占优势、各种频率的能量为多少,即信号的频率结构[7]。因此,为了获取更多信息,形成了谱估计和谱分析技术,功率谱分析是处理随机信号的一种有效方法,能反映信号各分量的频率构成情况,表达出不同频率信号的功率分布,从而辨识有用信号频率成分[8]。为更深入地了解液膜流动特性,本文通过MATLAB[9]内建功率谱密度计算函数对液膜波动的时间序列进行进一步的处理,获得液膜波动特性的功率谱密度(PSD)曲线,对不同Re下的液膜波动规律进行频谱分析,并结合概率密度分布(PDF)对液膜波形参数进行重新界定。
1 实验系统
实验系统如图1所示,包括液膜生成系统、数据采集系统、排出系统等,其中液膜通过侧面储水箱的窄缝漫溢产生。平面激光诱导荧光(PLIF)技术测量液膜厚度的光路为正交型,即入射激光垂直于液膜所在平板,并可通过调节激光器的位置来选择所需测量点,CCD摄像机则在与入射激光垂直的平板切线方向进行图像采集(图1),实验中CCD摄像机从上方进行拍摄,以方便光路垂直度的调节。实验选用最大吸收波长在555 nm的罗丹明 B作为荧光剂,并采用波长为532 nm的Nd:YAG激光器作为激发源,绿色激光连续输出。采用Photron FASTCAM SA5高速摄像机进行拍摄,在CCD镜头前加装高通滤光片,滤掉强度很大的绿色激光信号,进而只捕获橙色荧光信号。为了防止板壁侧面的储水箱中液体所发出的荧光对液膜厚度荧光信号产生干扰,实验时在储水箱上方贴黑色胶布。实验过程在暗室中进行,可避免其余光线的干扰,提高所捕获图像的清晰度。

图1 实验系统示意图
在液膜厚度识别中,因为拍摄时摄像机和液膜所流经的板壁都是固定的,而变化的只有液膜位置,因而将不同时刻拍摄的液膜实时图像进行记录,并利用数字图像处理软件对采集图像进行分析,可检测出液膜厚度的时序变化。实验中选用无液体波形板干板壁作为标定图像,则激光入射位置处的瞬时液膜厚度为:
δ=hn/m
其中:h为无液体干板壁的实际厚度,μm;m为板壁厚度图像的像素点数;n为激光入射位置处的某时刻液膜厚度图像的像素点数;δ为该时刻的瞬时液膜厚度,μm。
2 结果分析与讨论
2.1 实验结果误差分析
Re是决定液膜流动的重要参数,其定义如下:
Re=4Γ/μl
Γ为单位湿周的质量流量,即Γ=Ml/L,则:
Re=4Ml/μlL
其中:Ml为液膜质量流量,kg/s;μl为液膜动力黏性系数,Pa·s;L为液膜宽度,m。
本文以采集时间内液膜厚度的算术平均值作为该Re下的平均液膜厚度,即:
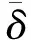

其中:ν为运动黏性系数,m2·s-1;g为重力加速度,m·s-2。
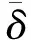

图2 液膜厚度实验值与拟合值的比较
2.2 液膜厚度的时序波动
为了更好地反映垂直下降液膜的波动特性,选择距液膜入口180 mm位置处作为测量点,在不同Re条件下对液膜厚度进行实时测量得到液膜厚度的时间序列(图3)。观察图3a发现,Re=123时,单位时间内表面波的数量很少,波动幅度也很小,说明低Re下液膜作小幅度波动。观察图3b、c,此时表面波数量有所增加,波动幅度基本一致,液膜波动的波形相对比较规则,接近周期正弦波。观察图3d,随Re的增加,各表面波的波动幅度开始出现差异,某些波的波幅大于其余波的,液膜表面波向数量少、幅度大的趋势发展。观察图3e、f发现某些波的波幅已远大于其余波的,波前很陡且前方分布着一些幅度较小的毛细波,因而两两大幅度波之间的液膜表面相对较平坦,呈驼峰状,称之为孤立波。

图3 液膜厚度的时序变化
2.3 液膜波动的谱分析
仅通过直接观察时间序列的规律很难确定液膜波动的频率结构等信息,利用幅域分析和频域分析则更加简单直观。本文基于MATLAB内建概率密度分布函数ksdensity对液膜厚度时间序列进一步处理,获得了实验工况不同Re下液膜波动的概率密度分布,如图4a~f所示,PDF曲线反映了液膜波动的幅域信息。在经典的周期图理论和Welch平均周期图方法的基础上,通过MATLAB内建功率谱密度计算函数得到了液膜厚度波动信号的功率谱密度曲线,如图4g~l所示,PSD曲线则反映了液膜波动的频谱特性。

图4 不同Re下液膜波动的概率密度分布与功率谱密度曲线
1) 幅域分析
图4a~f为实验工况不同Re下液膜波动的概率密度分布曲线。液膜波动的PDF曲线并不是一个对称图形,低Re下由于表面波数量较少,概率分布集中在一个较窄的区域内,波峰位置近似等于液膜厚度的时均值,波峰高且陡,说明此处液膜的波动很小,液膜厚度的分散性较小。随Re的增大,概率分布的主峰高度呈下降趋势,且主峰位置逐渐右移。
Re=187时,在较大的液膜厚度处出现第2波峰,说明随着波动的发展,表面波的数量增多使PDF曲线中较大液膜厚度出现的概率增加,但由于波幅基本一致,其PDF特征表现为第2波峰状。PDF的双峰特征是周期拟正弦波动的显著特征,可将其作为鉴别表面波波动特性的1个判据。
随Re的继续增大,液膜波动的PDF曲线的右侧区间越来越长。特别是从Re=617开始,孤立波的出现则使PDF的不对称性愈加严重且主要表现在较大的液膜厚度处。这表明此时液膜出现较大幅度的波动现象,且各表面波的幅度大小不一,从而导致液膜厚度的分散性大幅增加,液膜波动越来越剧烈。
2) 频域分析
图4g~l为实验工况不同Re下液膜波动的功率谱,如图4g所示,低Re时,功率谱曲线在30 Hz以内的频率区域分布较均匀,高频区域则陡然下降。这是因为小Re时液膜波动较小。
随Re的增大,功率谱波峰特征明显,如图4h所示,Re=187时,主峰频率为15 Hz左右,液膜波动的主要能量集中在4~20 Hz的频带区间内。这是因为此时表面波具有显著的周期性,波形近似规律正弦波,因而其波谱趋近于单一频率。
如图4i、j所示,从Re=265开始,功率谱的波峰特征变得不明显,说明液膜波动已不具备周期特性。已知PSD曲线下方所围面积代表该频率区间的波动所产生的能量,在低频区间PSD曲线所围面积增加,大幅度的低频波动开始作为液膜波动能量的来源之一。这其实是孤立波形成的初始阶段。
如图4k、l所示,功率谱已不具备波峰特征,在整个频带内均有分布,反映出液膜波动的多频特性。在2~20 Hz的频率区间内功率谱曲线高度基本保持不变,反映出孤立波数量少、波幅大、频性多的特征。由于孤立波携带了液膜波动的大部分能量,在大于20 Hz的高频区域PSD功率谱则呈现指数下降趋势。
功率谱分析表明,液膜波动具有显著的多频特性,且各频率有优劣之分,液膜波动的能量大多集中于低频区域,孤立波出现后,主能量所在的频带则更低。说明孤立波数量虽少,却携带着液膜波动的大部分能量,其对液膜波动能量的贡献不容忽视。结合液膜波动的PSD曲线与PDF曲线可对液膜波形参数进行界定,从而得出垂直下降液膜流动中波动幅度的变化规律。
2.4 液膜平均波高的界定及波动幅度的变化规律
波动幅度能反映表面波所携带的能量,是液膜波动特性的1个重要参数,但由于表面波形状的复杂性以及不同条件下的非线性演化,目前对这一参数的定义并无统一标准。大多研究者根据简单周期信号的振幅定义,将液膜的波动幅度简单定义为液膜厚度的最大值与时均液膜厚度之差[1]。而实际上不同于周期信号的单频结构,由图4g~l可看出,液膜厚度的波动具有显著的多频特性,而各频带内PSD曲线下方所围面积不同,则反映出各频带有优劣之分,即各频带内液膜的波动峰值对总能量的贡献是不同的,上面的定义并不合理。
Mouza等[10]将PDF波峰两侧5%区间内的平均液膜厚度定义为液膜的基底厚度;剔除掉PDF曲线两端的低频率液膜厚度,并将中间95%区间内的平均液膜厚度定义为液膜的平均波高,两者之差即为液膜的波动幅度。观察图4a~f中PDF特征曲线可知,液膜波动的PDF曲线并不是一对称图形,而孤立波的出现则使PDF的不对称性愈加严重,右侧区间越来越长。此时如果剔除PDF曲线两端5%区间的低频率液膜厚度,其中大部分将是孤立波这种大峰值波,而本文功率谱分析则表明,正是这种大幅度的驼峰状孤立波携带着液膜波动的主要能量,如果剔除将无法真实反映液膜波动特性。基于这一分析,本文对文献[10]中液膜平均波高进行了重新界定:将PDF曲线最左端5%区间内的小峰值液膜厚度剔除,剩余右侧95%区间内的平均液膜厚度则定义为液膜厚度波动的平均波高Hw,如图5所示,液膜的波动幅度ΔH定义为:
ΔH=Hw-Hs
实验针对不同Re下液膜厚度的时序变化进行了实时测量,其基底厚度Hs、平均波高Hw与波动幅度ΔH的变化趋势如图6、7所示。观察图6可发现,A区域,液膜的基底厚度基本不变,而平均波高一直随Re的增大而增大,所以图7中液膜的波动幅度ΔH与Re有强烈的相关性,随Re的增大而增大。这是因为Re较小时,液膜波动幅度很小,可看作是叠加在层流底层上的微小波动,此时流量的增加主要用来增大液膜的波动幅度。

图6 液膜的基底厚度与平均波高
如图7所示,B区域,液膜基底厚度的增长率突然增加,并与平均波高的增长率基本保持一致,因而此区域内液膜的波动幅度基本保持稳定。表明在这一流量范围内,液膜的基底厚度的增加与平均波高的增大达到一种平衡状态,其波动特性表现为近似稳定的周期波动,直至孤立波的出现打破了这种平衡。
C区域,孤立波的出现使液膜的扰动变得剧烈,如图6所示,液膜的平均波高大幅提高,而基底厚度的增长率基本保持不变。图7中液膜波动幅度显著增加,说明此时表面波所携带的能量大幅增加,液膜的波动不稳定性开始显现。这是由于驼峰状孤立波携带了大团流体,此时流量的增加主要用于孤立波数量的增加,对基底厚度的贡献则很少。

图7 液膜波动幅度变化
3 结论
本文利用激光诱导荧光技术结合CCD高速摄像采集系统得到自由下降波动液膜的实时图像,通过数字图像处理获得液膜厚度的时序变化。
1) 通过MATLAB内建函数的计算处理获得液膜厚度时间序列的PDF和PSD曲线,分别对液膜波动的幅域信息和频域信息进行分析。结果表明,液膜波动具有显著的多频特性。
2) PDF特征和PSD特征可作为判断液膜波动特性的判据之一。当Re=187时,表面波具有显著的周期性,波形近似规律正弦波,此时PDF曲线呈现双峰特性,而PSD曲线则表现出显著的波峰特征,即波谱趋近于单一频率。
3) 功率谱分析表明,液膜波动的能量大多集中于低频区域,孤立波出现后,主能量所在的频带则更低,说明驼峰波数量虽少,但其对液膜的波动能量的贡献却是不容忽视的。
4) 分析了液膜波动幅度随Re的变化规律:小Re时,液膜的波动幅度ΔH与Re有强烈的相关性,随Re的增大而增大;中等Re时,液膜的波动幅度基本保持稳定;大Re时,孤立波的出现使液膜波动幅度急剧增大,液膜波动不稳定性增强。
参考文献:
[1] DRAHOS J, TIHON J, SOBOLIK V, et al. Analysis of wave modes in liquid film falling down a vertical oscillating plate[J]. Chemical Engineering Science, 1997, 52(7): 1 163-1 176.
[2] LIU J, PAUL J D, GOLLUB J P. Measurements of the primary instabilities of film flows[J]. Fluid Mech, 1993, 250: 69-101.
[3] DROSOS E I P, PARAS S V, KARABELAS A J. Characteristics of developing free falling films at intermediate Reynolds and high Kapitza numbers[J]. International Journal of Multiphase Flow, 2004, 30: 853-876.
[4] 闫维平,李洪涛,叶学民,等. 垂直自由下降液膜厚度的瞬时无接触测量研究[J]. 热能动力工程,2007,22(4):380-384.
YAN Weiping, LI Hongtao, YE Xuemin, et al. A study of the transient non-contact measurement of vertical free-falling liquid-film thickness[J]. Journal of Engineering for Thermal Energy and Power, 2007, 22(4): 380-384(in Chinese).
[5] 郭斌,李会雄,郭笃鹏. 水平管外降膜流动液膜厚度的测量及分析[J]. 工程热物理学报,2011,32(1):71-74.
GUO Bin, LI Huixiong, GUO Dupeng. Mea-surement and analysis of the thickness distributions of falling liquid films around horizontal tubes[J]. Journal of Engineering Thermophysis, 2011, 32(1): 71-74(in Chinese).
[6] 古大田,朱家骅. 动态液膜厚度测试技术的研究[J]. 化工学报,1988(3):374-377.
GU Datian, ZHU Jiahua. A technique for measuring dynamic liquid film thickness[J]. Journal of Chemical Industry and Engineering, 1988(3): 374-377(in Chinese).
[7] 庄表中,陈乃力. 随机振动的理论及实例分析[M]. 北京:地震出版社,1985.
[8] 王经. 气液两相流动态特性的研究[M]. 上海:上海交通大学出版社,2012.
[9] 刘会灯,朱飞. MATLAB 编程基础与典型应用[M]. 北京:人民邮电出版社,2008.
[10] MOUZA A A, PANTZALI M N, PARAS S V. Falling film and flooding phenomena in small diameter vertical tubes: The influence of liquid properties[J]. Chemical Engineering Science, 2005, 60: 4 981-4 991.
