一类索赔相依二元风险模型下第n次索赔时的破产概率研究
2014-08-08王传玉张大伟
田 飞,王传玉,张大伟
(安徽工程大学 数理学院,安徽 芜湖 241000)
一类索赔相依二元风险模型下第n次索赔时的破产概率研究
田 飞,王传玉,张大伟
(安徽工程大学 数理学院,安徽 芜湖 241000)
在一类索赔相依二元风险模型下推导出了Gerber-Shiu函数满足的更新方程,以及破产时刻和直到破产时刻的索赔次数的联合密度函数,得到了第n次索赔时的破产概率的表达式。
二元风险模型;索赔次数;Laplace变换;破产概率
经典风险模型中,保险公司只面对单风险的情形;但现实生活中,保险公司会承担不同的保险业务,为了使风险模型更符合实际情况,赵晓芹[1]、张冕[2]等研究了一类索赔相依的二元风险模型的破产问题,此风险模型包含两种索赔:主索赔和由主索赔引起的副索赔;得到了此风险模型下生存概率所满足的微分方程,最后得到了最终破产概率渐进表达式,但是他们的文章中都没有涉及到索赔次数与破产时间之间的关系的问题,也没有考虑使用近年来被广泛使用的Gerber-Shiu函数来研究破产概率问题。而保险公司的风险来源主要是发生索赔的次数和发生索赔时的索赔额,确保保险公司稳定经营的一个重要衡量指标是破产概率,但是很少有学者对破产索赔次数与破产时间之间的关系进行研究。因此,将索赔次数和破产时间放在一起研究是一个比较新的和有意义的问题。
1998年Gerber and Shiu[3]定义了著名的期望折现罚金函数,后来被称之为Gerber-Shiu函数,他们首次把破产时间、破产前瞬时盈余和破产时刻赤字这3个重要精算变量嵌入到一个期望折现罚金函数中,通过求解该函数来研究三者的联合分布;近年来,破产时刻罚金折现期望已被用于一些实用的风险模型并由此产生了许多风险理论的新结论; Landriault[4]在2011年的文章中研究了服从指数索赔量的Sparre Andersen风险模型,使用Gerber-Shiu函数,他们推导出了Sparre Andersen风险模型下破产时刻和破产索赔次数的联合分布,并在服从指数索赔量的假设下推导出了含索赔次数的破产概率的表达式,这篇文章中的一个重要的想法就是一些关于破产时间的已知结果可以用破产时的索赔次数来解释;Dickson[5]在2012年的文章中使用概率论证的方法推导出了经典风险模型下破产时刻和破产索赔次数的联合分布,获得了破产索赔次数的概率函数的一般表达式。
本文在Dickson[5]的文章的基础上,研究了一类索赔相依二元风险模型下Gerber-Shiu函数满足的更新方程,推导出了一类索赔相依二元风险模型下破产时刻和直到破产时刻的索赔次数的联合密度函数,得到了第n次索赔时的破产概率的数学表达式。
1 预备知识
定义1 称pn(u)为初始盈余为u时,第n次索赔时的破产概率,即

定义2 由Dickson[5]我们定义了如下的Gerber-Shiu函数:
(1)
其中0 2.1 模型的建立 定义如下的盈余过程: 2.2 破产概率的求解 本节将在2.1所述独立二元风险模型下,根据(1)式,求出Gerber-Shiu函数满足的更新方程,进而求出破产概率。 考虑时间区间(0,T),其中t (2) 两边同时对T求微分,再令T=0,则有: (3) 这样我们就得到了独立二元风险模型下Gerber-Shiu函数满足的更新方程。 又由文献[6]可知,存在一个s满足以下鞅条件: 由这个条件我们可以得到独立二元风险模型下的广义Lundberg方程: (4) 定理1 当u=0时,独立二元风险模型第n次索赔时的破产概率为: (5) (6) 证明: 对(3)式两边同时作Laplace变换,有: (7) 由文献[3]和文献[6]可知,存在一个ρ,ρ使得方程 有唯一正解,将ρ代入(7)式,这样就有 (8) 由文献[4]可知: (9) 将(9)代入(8)式,化简整理可得: (10) 又 当u=0时,我们可以得到: (11) (12) 从而u=0时破产概率为: 对于u>0的情形,我们将在下一节讨论一类相依二元风险模型时进行分析,两种模型关于u>0的情形下破产概率的求解方法是类似的。 3.1 模型的建立 其中u≥0为常数,表示初始盈余; c为单位时间内的保费收入;N1(t)为主索赔发生的次数,它服从参数为λ的Poisson过程;N2(t)为副索赔发生的次数。 3.2 破产概率的求解 要求解3.1所述风险模型下的破产概率,我们先求出Gerber-Shiu函数满足的更新方程,以这个更新方程为基础,求出u=0和u>0两种情形下的破产概率的表达式。 引理1 3.1所述二元风险模型下Gerber-Shiu函数满足的更新方程为: (13) 证明:考虑一个很小的时间区间(0,h),其中t (1)在(0,h)上没有索赔发生; (2)在(0,h)上主索赔发生,且不引起副索赔发生; (3)在(0,h)上主索赔发生,且引起副索赔发生,且副索赔与主索赔同时发生; (4)在(0,h)上主索赔发生,且引起副索赔发生,且副索赔与主索赔不同时发生; 综上所述可得: 两边对h求微分,然后令h=0,得: 整理,即得证。 引理2 3.1所述二元风险模型下的Lundberg方程为: (14) 证明:由文献[6]可知,存在一个s满足以下鞅条件: 由 故 定理2 当u=0时,3.1所述二元风险模型下第n次索赔时的破产概率为 (15) (16) 证明:对引理1的(13)式作Laplace变换得: (17) 由文献[3]和文献[6]可知,存在一个ρ,ρ使得方程 有唯一正解,将ρ代入(17)式时,我们有: (18) 又由文献[4]可知: 代入(18)式,整理可得: 由(1)式可得: n=1 (19) (20) 从而有 对于u>0的情形,由文献[7]可知,对于一个很小的dt,ω1(u,t)dt表示在区间(t,t+dt)上发生首次索赔且导致破产发生的概率;对于这个事件,我们可以知道在时刻t之前没有索赔发生,在区间(t,t+dt)上有一次索赔发生,且索赔额超过u+ct,因此,由文献[7]可知: (21) 公式(19)是这个式子的一个特殊情况,类似地,我们可以得到 (22) 我们用ωn+1(u,t)dt表示在区间(t,t+dt)发生第n+1次索赔,且导致破产发生的概率。假设在时刻t之前有n次索赔发生,总索赔额为u+ct-x,因此在时刻t的盈余为x,如果在区间(t,t+dt)上有一次索赔额超过x的索赔事件发生,则会导致破产的发生,即为(22)式的第1项和第2项之和;但这种情况没有考虑在时刻t之前盈余小于0的情形。假设在时刻s(0 本文研究独立二元风险模型和一类索赔相依二元风险模型,通过构造一个特殊的Gerber-Shiu函数,推导出了两类二元风险模型下Gerber-Shiu函数满足的更新方程,由这个更新方程推导出破产时刻和直到破产时刻的索赔次数的联合密度函数,最终得到两类风险模型下第n次索赔时的破产概率的表达式。 [1] 赵晓芹.一类索赔到达计数过程相依的二元风险模型[J].数学的实践与认识,2006,36(2):42-45. [2] 张冕.一类索赔相依二元风险模型的破产概率问题研究[J].经济数学,2008,25(2):132-135. [3] Gerber H U, Shiu E S W. On the time value of ruin[J].North American Actuarial Journal, 1998,2(1):48-78. [4] Landriault D, Shi T, Willmot G E. Joint density involving the time to ruin in the Sparre Andersen risk model under exponential assumptions[J].Insurance:Mathe-matics and Economics, 2011,49:371-379. [5] Dickson D C M. The joint distribution of the time to ruin and the number of claims until ruin in the classical risk model[J].Insurance: Mathematics and Economics,2012,50:334-337. [6] Hélène Cossette, Etienne Marceau. On the compound Poisson risk model with dep -endence based on a generalized Farlie-Gumbel-Morgenstern copula[J].Insurance:Mathematics and Economics, 2008,43:444-455. [7] Dickson D C M. Some finite time ruin problems[J].Annals of Actuarial Science,2007,2:217-232. (责任编辑:张英健) The Probability of Ruin at the nthClaim with Correlative Claim in Dual Risk Modle TIAN Fei,WANG Chuanyu,ZHANG Dawei (College of Math & Phy, Anhui Polytechnic University, Wuhu Anhui 241000, China) For the dual risk model for correlative claim, we derive the renewal equation of the Gerber-Shiu function by constructing a peculiar Gerber-Shiu function, obtain the joint probability density function of the time to ruin and the number of claims until ruin, and find the formula of ruin probability when riun occurs at the time of the nthclaim. dual risk modle; the number of claims; Laplace transform; ruin probability 2014-01-10 国家自然科学基金项目(61203139);安徽省重点教研项目(2012jyxm277) 田飞(1988-),男,湖南怀化人,硕士生,主要研究方向为精算数学。 O211.9 A 1671-5322(2014)02-0011-052 独立二元风险模型的破产概率

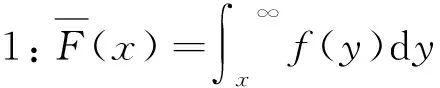






3 一类索赔相依情形下的二元风险模型的破产概率


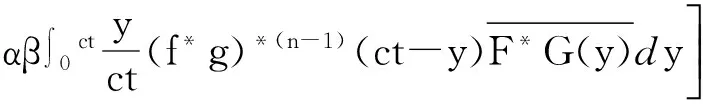

4 结语
