双弹性管流固耦合振动的数值模拟

冯志鹏，臧峰刚，张毅雄

(中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041)

管束类结构的流固耦合振动在海洋工程、航天航空、核工程等领域中非常普遍。运行经验和科学研究结果表明，流致振动是导致蒸汽发生器传热管破裂失效的关键因素，由其导致的传热管破裂将会影响核电站运行的可靠性。因此，对流体诱发的弹性管振动进行深入研究十分必要。

不同排列的双管是实际应用中最基本的组合单元，Sumner等[1]、Price等[2]通过实验研究了串列与交错排列双管的涡激振动；Antoine等[3]采用梁方程模拟直管，联合Star-CD研究了单圆柱与流体的相互作用；Liu等[4]采用有限元方法和可变形网格技术对Re=200的并列弹性支撑刚性双圆柱涡激振动进行了数值模拟；Lam等[5]采用表面涡方法对Re=2.67×104下小节径比一列和错列的阵列圆柱的流致振动进行模拟，指出在大幅值振动时流致振动对横向振动的影响不可忽略；Longattea等[6]提出了一种采用ALE方法的流致振动数值模型，但该模型只能预测横流中弹性支撑刚性管的振动频率，无法考虑湍流与管的变形。已有的这些研究，主要针对弹性支撑刚性管，而对三维弹性管束与流体相互作用的研究相对较少。当考虑管束的弹性变形时，由于流体流动和管道运动间的相互作用、流场与结构的相互作用变得更复杂，振动特性与流场特征通常与节径比、排列方式、流动速度等相关。

本文采用双向流固耦合方法，结合动网格控制技术，同时考虑流体-结构两个物理场间的相互作用，联合计算流体力学和计算结构动力学建立三维弹性管束的流固耦合振动模型，研究双弹性管的流固耦合振动，旨在为自主设计蒸汽发生器传热管束的流致振动分析提供技术支持。

1 数值模型

1.1 CFD模型

在预测管束的横掠问题中，较先进的RANS(雷诺平均N-S方程)湍流模型，如可实现k-ε和RNGk-ε模型均极大地低估了密集管束中的湍动能强度，而LES(大涡模拟)的结果与DNS(直接模拟)和实验结果吻合较好[7]，可得到RANS无法获得的湍流结构，因此本文采用大涡模拟方法来计算流体区域。连续性方程及动量守恒方程在物理空间经滤波后可得到大涡模拟的控制方程：

(1)

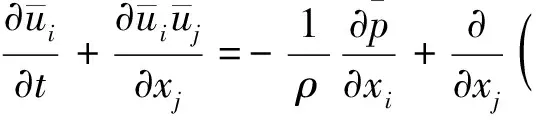
(2)

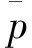
流场区域及网格如图1所示，其中D为管子外径，流体域网格为六面体结构化网格。图1中左边入口采用速度入口边界条件，右端出口采用压力出口边界条件，其他外边界按对称边界和固定壁面处理；管壁面为流固耦合交界面，设为动网格边界。

1.2 结构分析模型

管的结构参数取为：管长0.5 m；外径D=0.01 m；内径0.009 5 m；弹性模量E=1×105MPa；泊松比υ=0.3；密度ρs=6 500 kg/m3；阻尼系数α=5.098，β=0.000 215。

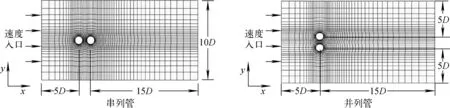
图1 流场区域及网格示意图

利用有限元方法对管结构进行离散，即可得到每个管的质量矩阵与刚度矩阵[8]。采用Newmark数值积分方法求解结构动力学方程，进行瞬态动力学分析：

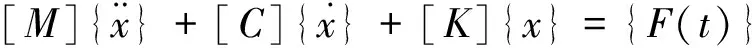
(3)

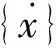
1.3 动网格模型

采用基于扩散光顺(Diffusion-Based Smooth)方法的动网格模型来控制运动边界的网格更新，其网格运动由式(4)的扩散方程控制。

·(γ

(4)

式中：u为网格移动的速度，在变形边界上网格的运动与边界相切；γ为扩散系数，表示为单元体积的函数，γ=1/Vα，用于控制边界网格对内部网格的影响，α为控制参数，本文取2。式(4)用有限体积法离散并迭代求解，单元中心的移动速度u通过距离加权平均插值到各网格节点，根据式(5)即可更新节点位置：

xnew=xold+uΔt

(5)

1.4 流体-结构间的耦合

通过流固耦合交界面进行固体域和流体域间的数据传递，将计算结构动力学(CSD)和计算流体动力学(CFD)联合。CSD通过计算结构位移来指定流体域的变形，而用CFD计算作用在结构上的载荷，结构域和流体域间的双向耦合通过采用相同时间步的流体计算和结构动力学计算依次迭代实现。

1) 用Newmark算法求解结构动力学方程，得到结构的位移、速度等参数，将结构的位移与速度传递给动网格求解器。

2) 动网格求解器根据结构位移更新流体域网格。

3) CFD求解，得到流场的u、v、w和压力场p等流场参数，并将作用在结构上的流体载荷传递给结构求解器。

4) 回到1，进行下一时间步求解。

流体力虽不是一连续函数，但可在每个时间步结束时，通过流体求解器得到一瞬时值，从而更新当前结构的位置，并得到下一时间步的流体计算网格。

2 结果分析

为表述方便，定义以下无量纲变量：升力系数均方根ClRMS=FlRMS/(0.5ρAU2)，阻力系数均方根CdRMS=FdRMS/(0.5ρAU2)，其中FdRMS、FlRMS分别为阻力Fd与升力Fl的均方根值；流向位移x/D、横向位移y/D；流向振幅Ax/D=xRMS/D，横向振幅Ay/D=yRMS/D，其中xRMS、yRMS分别为流向振动位移与横向振动位移的均方根值；涡脱频率St=fstD/U；间隙流速Upr=Up/(fnD)，Up=UP/(P-D)，其中P/(P-D)为节径比，U为来流速度，D为管外径，P为两管的间距，fn为管的固有频率，fst为静止圆柱体绕流的泻涡频率；A为所要计算方向上的投影面积。

2.1 模型验证

为验证数值模型，计算了单根弹性管的流致振动。图2中分别就数值计算得到的管的振动频率fex与固有频率fn之比fex/fn及横向振幅Ay/D随来流速度(无量纲)Ur(Ur=U/fnD)的变化情况与已有实验结果[3]进行了比较，通过比较可看到，两者在趋势和数值上吻合较好，说明本文的流体-结构交互作用模型是可行的和正确的。

2.2 临界间距

1) 两串列管

为研究两串列管的交互作用，建立了如图3所示的两串列管，其中管2位于管1尾部的下游，流向间距Px的变化范围为1.2D～4D。

图4示出了阻力系数均方根CdRMS、升力系数均方根ClRMS与振幅随节径比的变化情况。管1、管2与单管间的相互比较分析可发现：(1) 振幅随节径比的变化趋势与流体力随节径比的变化趋势相同，两串列管的临界间距为2D。(2) 当Px/D>2时，管1几乎不受管2的影响，其流体力、振幅与单管接近，管2的CdRMS远小于管1与单管的，但随节径比的增加，管2的CdRMS迅速增加到约为单管的0.5倍；由于管1尾流的影响，管2的ClRMS与Ay/D均大于单管的，且随节径比的增大而增大，当Px/D=4时，管2的ClRMS约是管1的4倍，振幅约是管1的5倍。(3) 当Px/D≤2时，两串列管的ClRMS与振幅均接近单管，而两串列管的CdRMS则小于单管的，管1约为单管的0.8倍，管2仅为单管的0.1倍。

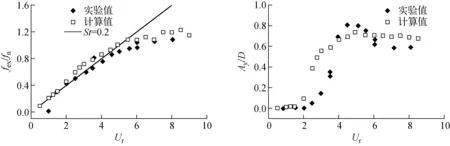
图2 振动响应随Ur的变化情况

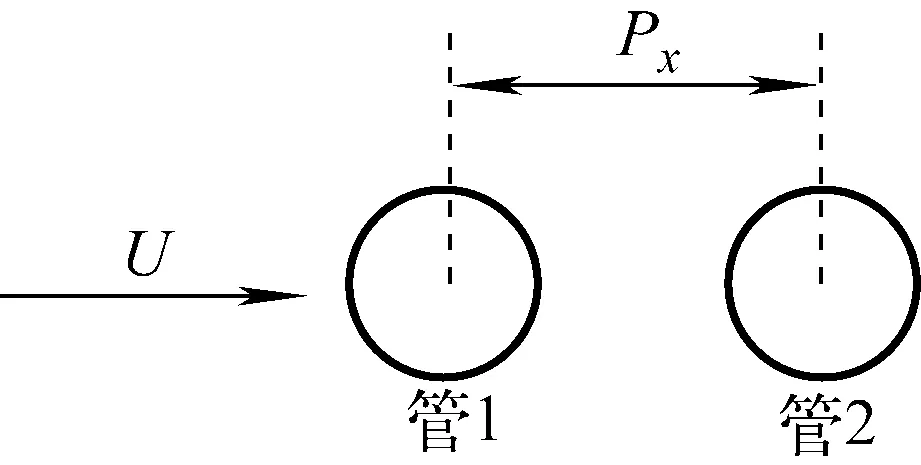
图3 串列管示意图

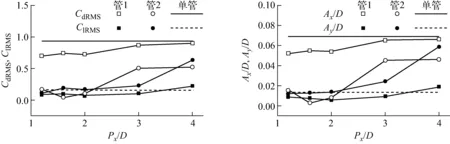
图4 阻力系数、升力系数均方根和振幅随节径比的变化

显然，流体力、振幅与节径比密切相关，当节径比小于临界值(Px/D≤2)时，管1与管2的横向变量(升力、横向振幅)均较小，接近于单管，而当节径比大于临界值时，管2的横向变量远大于管1与单管的；下游管2与上游管1间的Ay/D随节径比的增大而增大。

2) 两并列管

为研究横流中两并列管间的相互作用，建立了如图5所示的参数完全相同的两并列管，横向间距记为Py。由于并列管中管1与管2的升力与横向振幅相等、相位相反，阻力与流向振幅基本相同，因此只取管1进行分析。

图5 并列管示意图

图6a示出两并列管CdRMS、ClRMS随节径比的变化，图6b显示了振动幅值随节径比的变化，并分别与单管的进行了比较。可看到，CdRMS和ClRMS随Py/D的减小而增加，振幅随间距的增加而呈非线性趋势减小，同时还发现当间距大于一临界间距(3D)后，两管间基本不再相互影响，ClRMS与Ay/D与单管的接近。当间距较小时，两管的流场强烈耦合，漩涡激发振动和流体弹性不稳定性均可能导致两管相互碰撞。

2.3 临界流速

通过对不同节径比的两串列管、两并列管的流致振动分析发现，并列管、串列管的振动特性会在其临界间距发生较大的转变，以下分别以P/D=1.6与P/D=3为例分析流速与两弹性管的流固耦合振动间的关系，其中P/D=1.6的两并列管会在Upr>4时发生碰撞。

图7为串列管与并列管的CdRMS和ClRMS随Upr的变化。从图7a可看出，CdRMS随Upr的增大先减小再增加到一较恒定值。从图7b可看出，P/D=3的两串列管、P/D=1.6与P/D=3的两并列管ClRMS随Upr的增大先减小再增加，达到最大值后迅速下落；而对P/D=1.6的两串列管，其ClRMS随Upr的增大而增大，达到最大值后也迅速下落。

图8为串列管与并列管的流向振幅Ax/D与横向振幅Ay/D随Upr的变化。通过综合比较图7、8可得出，P/D=3的串列管1、并列管的CdRMS、ClRMS、Ax/D、Ay/D与串列管2的ClRMS、Ay/D开始急剧增加的速度为Upr=3，只

有处于下游串列管2的流向变量——CdRMS与Ax/D开始大幅增加的速度发生在Upr=4。P/D=1.6的串列管与并列管的CdRMS最小值均在Upr=4，ClRMS、Ax/D、Ay/D开始急剧增加的速度也在Upr=4。因此，P/D=3的双管的临界流速为Upr=3，P/D=1.6的双管的临界流速为Upr=4。通过仔细比较串列管1、串列管2与并列管在相同条件下的流体力系数及振幅，可发现，双管的临界速度与节径比相关，而排列方式对其影响不大。相同节径比情况下，并列管的振动较串列管强烈，受到的流体力更大，振幅也大于串列管的。

综上所述，当节径比大于临界节径比(如P/D=3)时，两弹性管的流体力系数随Upr的变化曲线存在一最小值，其恰好对应振幅开始急剧增加的流速，此时的流速即为临界流速。在临界流速以下，流体力系数随间距的减小而增大，而在临界流速以上，CdRMS则随Upr的增加先减小再增大到一较恒定值，ClRMS随Upr的增加先减小再增大，在达到最大值后迅速下落。

当节径比小于临界节径比时(如P/D=1.6)，CdRMS随Upr的变化曲线存在一最小值，其随Upr的增加先减小再增大到一较恒定值，而ClRMS随Upr的增加而增大，达到最大值后迅速下落。

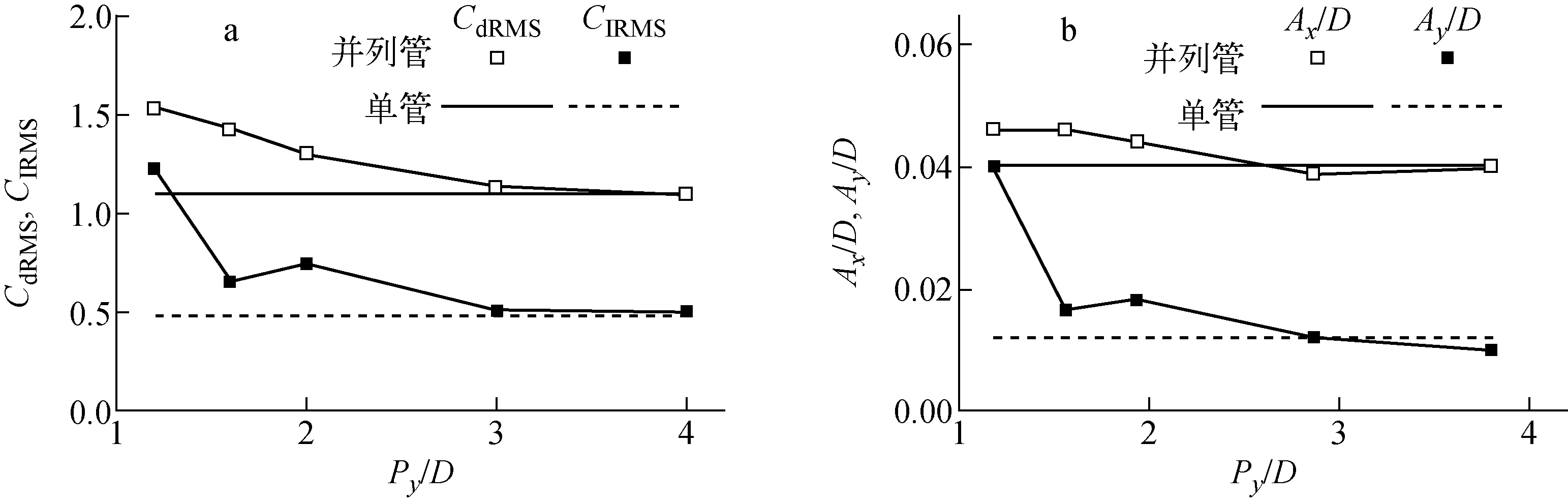
图6 阻力系数、升力系数均方根(a)和振幅(b)与节径比的关系

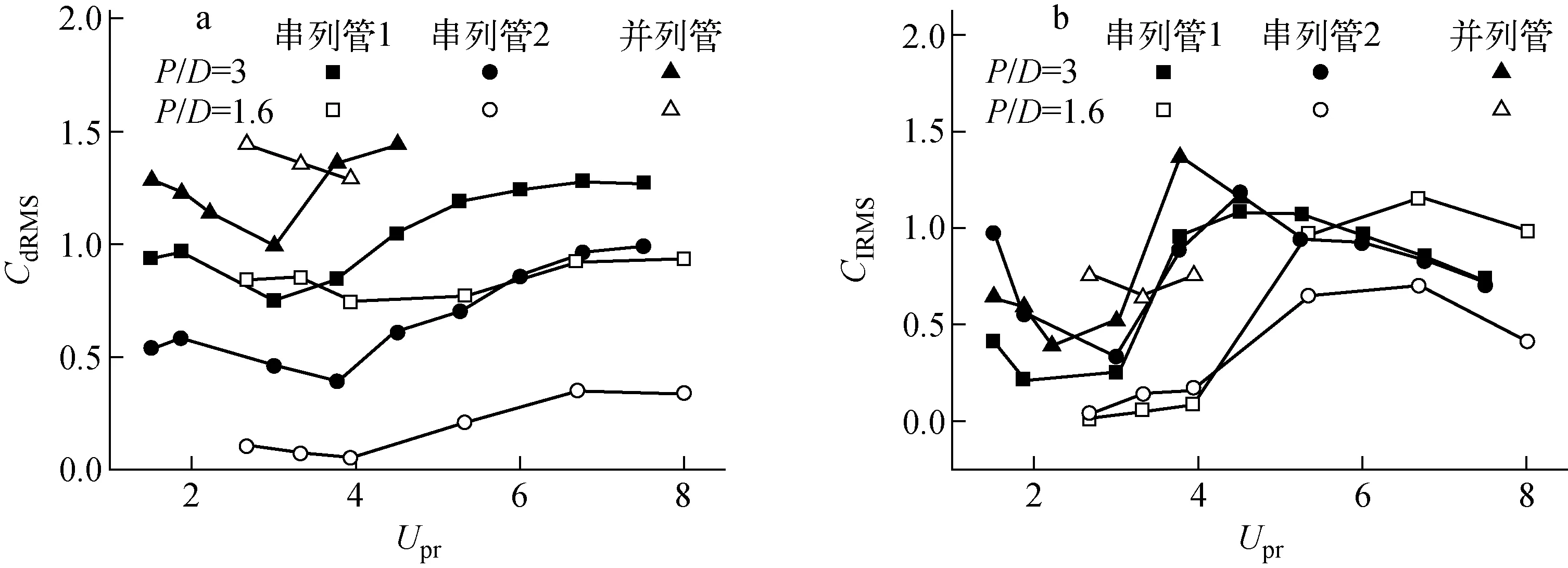
图7 CdRMS(a)和ClRMS(b)随Upr的变化

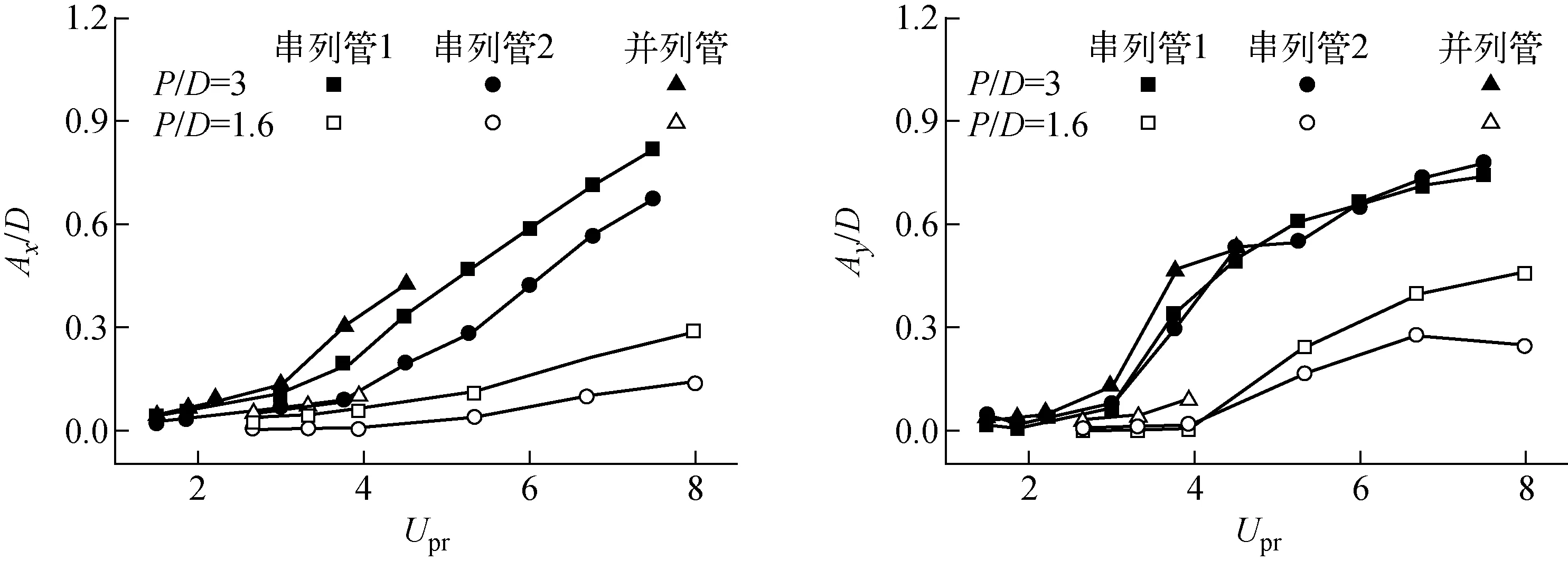
图8 Ax/D和Ay/D随Upr的变化

流向与横向振幅均随Upr的增加而增加。

2.4 运动轨迹

通过流体力系数均方根及振幅响应随Upr的变化可知，P/D=3和P/D=1.6两种节径比管束的临界流速分别为Upr=3和Upr=4，因此以下分别取低于临界速度和高于临界速度两种情况进行分析。对P/D=3，取Upr=2.2与Upr=3.8；而对P/D=1.6，由于两并列管在Upr>4时发生碰撞，因此取Upr=2.7与Upr=4。

1) 两串列管

对不同间距的两串列管来说，当流速低于临界流速时，串列管的振动很小，运动轨迹紊乱；当流速高于临界流速时，两管开始在流向和横向发生大幅振动，运动轨迹为“8”字形图，如图9所示，阻力使运动轨迹向下游方向弯曲，上游管1的振幅较下游管2的大。另外，从图9还可发现，当间距大于临界间距后，两管的运动轨迹与相同情况下单管的类似，两管间的相互影响较弱，而当间距小于临界间距时，两管间的相互作用明显较强烈，如图9a、b所示。

2) 两并列管

不同间距两并列管在临界流速内的响应与串列管类似，但在临界流速外的运动轨迹与串列管明显不同，且与节径比相关。临界间距内(如P/D=1.6)的两并列管在较高流速时的运动轨迹为如图9c所示的椭圆形；而临界间距外的两并列管(如P/D=3)，其在高于临界流速的流体作用下的运动轨迹如图9d所示，与相同情况下两串列管的不同，其轨迹不是“8”字形，而为类似“小雨滴”的形状。从图9c、d中也可看到，两并列管的横向运动相位相反，幅值相等。

2.5 尾涡结构

1) 两串列管

P/D=1.6和P/D=3两串列管的尾涡结构示于图10。从图10a、b可看出，在临界间距内的两串列管的流场场结构与单管的类似，漩涡间距较小，强度也较低，尾涡尺度随流速的增加而有所增大，上游管1无稳定的涡脱落。从图10c、d可看出，当间距大于临界间距时，两管均有涡脱落，且尾涡结构会在临界流速发生显著改变，在低速时，串列管2后的尾涡模态与单管的类似，但当流速较高时，在串列管2的后面出现了两排平行的涡，尾涡的横向间距明显增大。

a、c——P/D=1.6,Upr=4；b、d——P/D=3,Upr=3.8

2) 两并列管

P/D=1.6和P/D=3两并列管的尾涡结构示于图11。从图11a、b可看出，当Upr=2.7时，漩涡分别在管1与管2各自尾部的1.5D范围内形成和脱落，但沿着流向的发展，其尾涡相互干扰并合并，在1.5D后，尾涡合并为单排的、交替的漩涡。从图11c、d可看出，流速较低时，在管1与管2的后面形成几乎独立的涡街，而当流速较高时，管1与管2会在其尾部分别形成两排平行的旋涡，且两管后面的涡会在尾流中间相互挤压和干扰，涡的横向间距也明显增大。从尾涡结构中也可看到并列管尾涡相位相反的现象。

图10 P/D=1.6(a、b)和P/D=3(c、d)两串列管的尾涡结构

图11 P/D=1.6(a、b)和P/D=3(c、d)两并列管的尾涡结构

3 结论

1) 两串列管的临界间距为2D，两并列管的临界间距为3D。2) 在临界间距内，两弹性管相互影响，而当间距大于临界间距后，两管间的相互影响基本消失，响应与单管的接近；两串列管的下游管与上游管间的横向振幅比值随间距的增大而增大，两并列管的流体力与振幅随着间距的增加呈非线性趋势减小。3) 当流速高于临界流速时，两串列管的运动轨迹均为“8”字形图，而间距大于临界间距的两并列管的运动轨迹为类似“小雨滴”形，间距小于临界间距的两并列的运动轨迹为椭圆形；当流速低于临界流速时，两串列管与两并列管的振动均很小，运动轨迹紊乱。4) 在临界流速或临界间距内，串列的下游管、并列的两管的尾涡均为独立的涡街；而在临界流速与临界间距以外，则会在串列的下游管与并列的两管尾部分别形成两排平行的涡街。

参考文献：

[1] SUMNER D, RICHARDS M D, AKOSILE O O. Two staggered circular cylinders of equal diameter in cross-flow[J]. Journal of Fluids and Structures, 2005, 20: 255-276.

[2] PRICE S J, PAIDOUSSIS M P, KRISHNAMOORTHY S. Cross-flow past a pair of nearly in-line cylinders with the upstream cylinder subjected to a transverse harmonic oscillation[J]. Journal of Fluids and Structures, 2007, 23: 39-57.

[3] ANTOINE P, SIGIST J F, HAMDOUNI A. Numerical simulation of an oscillating cylinder in a cross-flow at low Reynolds number: Forced and free oscillations[J]. Computers & Fluids, 2009, 38: 80-100.

[4] LIU Y, SO R M C, LAU Y L, et al. Numerical studies of two side-by-side elastic cylinders in a cross-flow[J]. Journal of Fluids and Structures, 2001, 15: 1 009-1 030.

[5] LAM K, JIANG G D, LIU Y, et al. Simulation of cross-flow-induced vibration of cylinder arrays by surface vorticity method[J]. Journal of Fluids and Structures, 2006, 22: 1 113-1 311.

[6] LONGATTEA E, BENDJEDDOUB Z, SOULIB M. Methods for numerical study of tube bundle vibrations in cross-flows[J]. Journal of Fluids and Structures, 2003, 18: 513-528.

[7] BENHAMADOUCHE S, LAURENCE D. LES, coarse LES, and transient RANS comparisons on the flow across a tube bundle[J]. International Journal of Heat and Fluid Flow, 2003, 24: 470-479.

[8] 王勖成. 有限单元法[M]. 北京：清华大学出版社,2003:468-495.