棒束通道内过冷沸腾起始点的实验研究
2014-08-08周云龙侯延栋李洪伟
周云龙,侯延栋,李洪伟
(东北电力大学 能源与动力工程学院,吉林省 吉林市 132012)
棒束通道内的沸腾流动广泛存在于动力工程、石油化工、核能等领域[1-2]。在加热的过冷通道内,通常把过冷沸腾起始点(ONB)看作是单相流动和两相流动换热的重要转折点,此点上游单相流动换热占主导地位,下游由于气泡的产生,传热机制发生很大变化,在沸水堆内还会对中子的慢化产生重要影响。因此,准确确定棒束通道内的ONB,对棒束通道内的传热、压降计算和反应堆安全分析具有重要意义。
迄今为止,各国学者对平板、环形、矩形窄缝等通道内的ONB进行了实验研究和理论分析。Hsu[3]第1次提出了沸腾起始的条件,认为当出现气泡时,气泡尾部的温度至少等于气泡内部压力所对应的饱和温度。Bergles等[4]对单内管加热的环形通道内的ONB进行了实验研究,通过拟合实验数据得到了ONB的热流密度经验关系式。苏顺玉等[5]在强迫流动沸腾条件下对环形狭缝通道内的ONB进行了研究。Basu等[6]对1个铜平板表面和锆-4合金构成的3×3棒束通道内的ONB进行研究,并用Bergles等、Sato等、Davis等的经验关系式与实验数据进行了对比。王甲强等[7]对环形窄缝通道内双面加热的ONB进行了研究,得出了1个适用于环形窄缝通道内ONB的经验关系式。
本文研究棒束通道内ONB的质量流速、进口欠热度、棒束几何尺寸对热流密度的影响,并据此提出计算棒束通道内ONB热流密度的关系式。
1 实验装置
1.1 实验回路
实验回路如图1所示,通过离心泵把实验用的流体工质去离子水从水箱输送至预热器,经预热器加热至预定温度后进入可透视实验段,对其中的两相流流型以及转换过程进行观察和高速摄像。然后,气液两相混合物从实验段出来进入汽液分离器分离,分离出的蒸汽经冷凝器两次冷凝后与分离出的液态工质汇合后再冷凝一次,返回到水箱。

图1 实验系统示意图
1.2 实验段
实验段结构如图2所示,实验段由加热棒束和套管组成。9根不锈钢加热棒呈正方形排列,置于套管中,构成实验通道。加热棒束长1 000 mm,底部300 mm和顶部100 mm为非加热段,中间600 mm为有效加热段,可通过调节电压和电流控制加热功率;加热棒外径为10 mm,栅距为15 mm。套管长1.2 m,内径60 mm,外径70 mm。为了增加实验数据的准确性,加热棒均经过严格的打磨,表面光滑,无污垢,无凹坑和碰撞疤痕等。

图2 实验段结构示意图
在实验段上共设置7个测温截面,每个测温截面与流体进口的距离分别为300、400、500、600、700、800、900 mm,每个测温截面上设3个测温点,用以测量对应的3个局部壁面温度。工质进出口温度分别由安装在进出口管路上的热电偶测得。本实验中所有温度均采用K型热电偶测量。实验段上共开3个测压孔,测压孔位置分别距进口300、600、900 mm,如图2所示。除此之外,在实验段对应的套管位置上开两个对称的视镜口,镶嵌石英玻璃,在实验过程中可用高速摄影装置拍摄流型。
本实验的实验条件为:实验段出口压力为0.1~0.11 MPa,实验段进口流体温度为80~100 ℃,质量流速为0~100 kg/(m2·s),热流密度为0~80 kW/m2。
2 实验方法及数据处理
2.1 实验方法
实验回路准备就绪后,在水箱内充满水,用电加热器加热3 h进行除气,然后冷却到实验要求的温度。实验中,调节流量阀门得到所需流量,调节预热段功率,达到预设的进口欠热度,然后保持压力、质量流量和进口欠热度不变,改变实验段热流密度,记录棒束壁面热电偶测点处壁面温度的变化。随着热流密度的逐渐增大,该点处的壁面温度逐渐增高,流体温度从过冷达到饱和。用数据采集器记录不同热流密度对应的壁面温度变化和实验段的电流、电压,得到1组实验工况。
在ONB之前单相流体强制对流换热占主导地位,壁面温度随流体温度的增高而近似呈线性增长;当出现ONB之后,由于气泡的产生,对流换热系数陡增,壁面温度变化不再是线性增长,而是随热流密度的增大缓慢增长,甚至有可能出现下降的趋势。因此,ONB可认为是壁面温度曲线中流体饱和温度之后壁面温度突然发生阶跃变化的点[8-9]。
2.2 数据处理
根据采集到的电流和电压,利用式(1)计算实验段的热流密度qe:
qe=ηeUeIe/(9πdl)
(1)
式中:Ue为实验段电源的电压;Ie为实验段电源的电流;d为加热棒直径;l为加热棒有效加热长度;ηe为实验段的加热效率,其值在实验前的热平衡实验中获得。
测量截面的平均壁面温度计算如下:
tw=(t1+t2+t3)/3
(2)
式中:tw为测量截面的平均壁面温度;t1、t2、t3分别为截面上加热棒不同位置处的温度。
为更好地说明预测值与实验值之间的误差,采用相对误差MRE来说明经验关系式的预测精度。MRE的计算公式如下:
(3)
式中:N为数据个数;qExp,i为热流密度实验值;qPre,i为热流密度预测值。
3 实验结果分析
3.1 ONB的确定
图3示出不同工况下壁面温度随热流密度的变化。采用最小二乘法分别对单相流动段及过冷沸腾段热流密度与壁面过热度之间的关系进行拟合,拟合出的两曲线的交点即是ONB,从交点位置即可得到产生ONB的壁面过热度和热流密度。实验共得到了96组ONB数据。

图3 壁面温度与热流密度的关系
3.2 热工参数对ONB的影响
1) 子通道对ONB壁面温度的影响
从图2可看出,整个流动通道可划分为不同的子通道1、2、3。不同子通道所处的位置不同,其通道内对流体的加热程度存在差异,造成不同通道内加热棒的壁面温度存在差异。不同子通道对ONB的壁面温度的影响示于图4。从图4可看出,在相同进口温度、流量、热流密度下,子通道3处于棒束中心,对流体的加热量最大,先出现ONB;子通道1处于最边缘,对流体的加热量最小,最后出现ONB。此外,子通道1、2、3内的ONB的壁面过热度分别为:4.1~5.6、3.4.~4.8、2.1~3.6 ℃,整个实验中ONB的壁面过热度为2.1~5.6 ℃,与Basu等[10]得出的ONB壁面过热度范围(1.8~5 ℃)基本一致。

图4 不同子通道对ONB壁面温度的影响
2) 流量对ONB热流密度的影响
流量对ONB热流密度的影响示于图5。从图5可看出,当进口欠热度Δtsub一定时,流量越大,棒束内ONB的热流密度越大。这是因为流量越大流速就越快,流体能对棒束进行较好的冷却,导致壁面过热度减小,不能使流体过冷沸腾,就需较大的热流密度才能使流体沸腾。因此,随着流量的增大,ONB的热流密度逐渐增大,这一点在Basu等的实验中已得到证实。

图5 流量对ONB热流密度的影响
3) 进口欠热度对ONB的影响

图6 进口欠热度对ONB的影响
进口欠热度对ONB的影响示于图6。由图6可看出,当流量、压力一定时,随着进口欠热度的逐渐增大,在棒束同一截面位置,ONB的热流密度逐渐增大。这是由于在相同的压力、流量条件下,进口欠热度越小,流体对棒束的冷却越不充分,导致棒束壁面的过热度相对较大,先达到ONB的壁面过热度,因此进口欠热度小时ONB的热流密度较小。此外,随着轴向距离的增加,截面越靠后,ONB的热流密度越小,这是由于截面越靠后,流体受到棒束的持续加热欠热度较小,这一点在Basu等的实验中也得到验证。
3.3 ONB的热流密度关系式
目前的ONB热流密度关系式大多是针对于圆管提出的,若将这些关系式直接应用于棒束通道将存在很大误差,这一点已被Basu等证实。常用的Bergles等的关系式如下:
qONB=1.798×
10-3p1.156(1.8(tw-tsat))2.282/p0.023 4
(4)
式中:qONB为ONB的热流密度;tsat为对应压力下的饱和温度。
Bergles等的关系式预测值与实验值的对比示于图7。从图7可看出,Bergles 等的关系式对于棒束通道ONB的热流密度预测误差很大,其相对误差为40.36%。基于此,本文提出一针对于棒束通道ONB的热流密度关系式。由于棒束通道的特殊几何结构,对流动和传热有很大影响,因此,除热工参数对ONB的热流密度的影响外,还应考虑棒束几何结构对ONB的热流密度的影响,由于质量流速和流道间隙对棒束通道内的沸腾传热和流动的影响可用雷诺数Re来反映,为此引入Re来反映棒束几何结构和质量流速的影响。按照Bergles等的关系式,得到新的关系式为:
qONB=C1ReC2pC3(1.8(tw-tsat))2.282/p0.023 4
(5)
式中,C1、C2、C3为修正系数。根据不同实验工况下棒束通道内ONB的热流密度的实验值,对所测数据进行非线性回归分析,得到C1=2.976 50×10-3,C2=-0.049 6,C3=1.156。

图7 Bergles等的关系式预测值与实验值的对比
由式(5)得到的预测值与实验值的对比示于图8。由图8可见,新的关系式能很好地预测ONB的热流密度,其预测值的相对误差为14.75%,与Bergles等的关系式相比,预测结果更加准确。
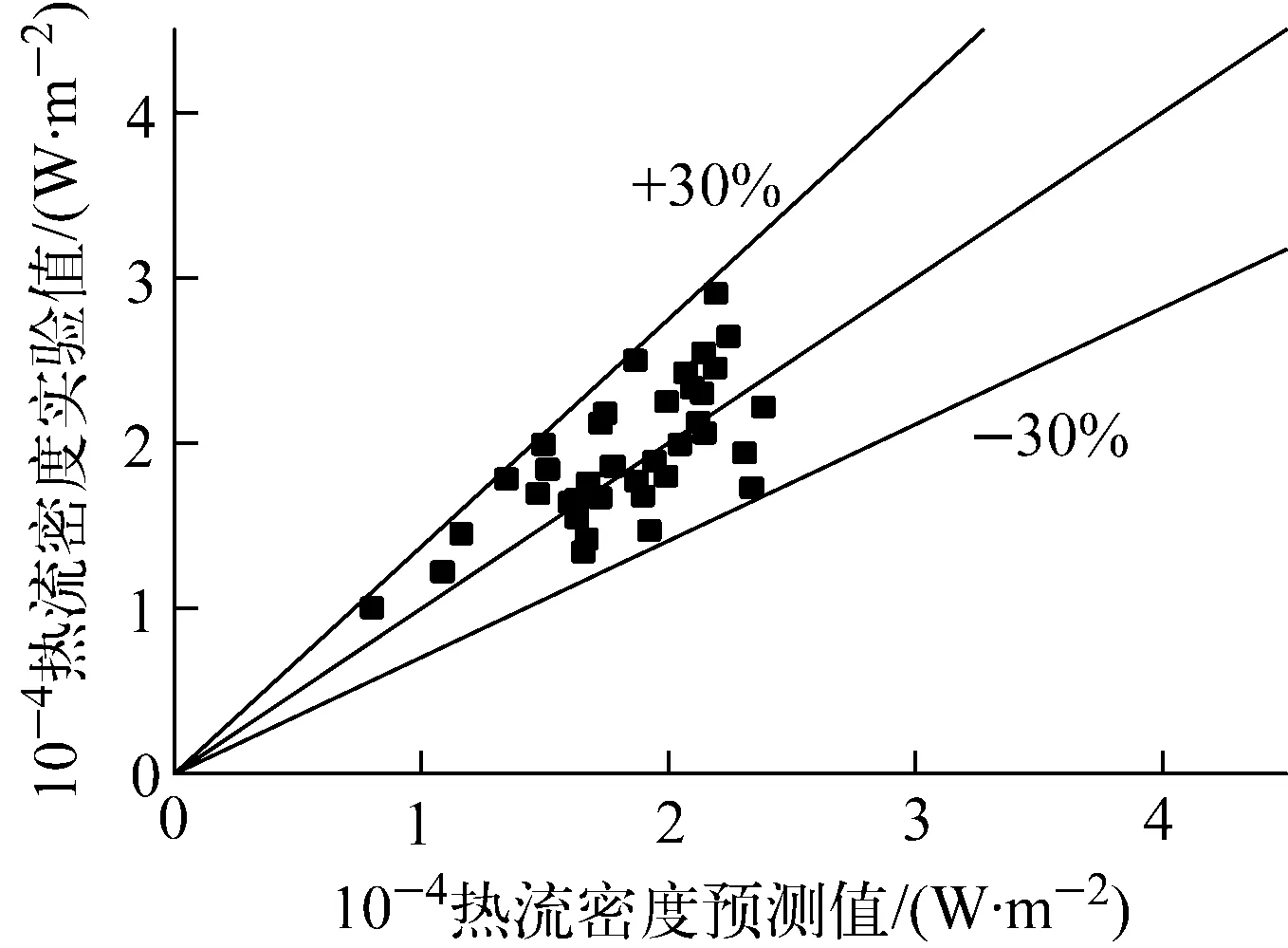
图8 改进的关系式预测值与实验值的对比
4 结论
1) 棒束通道内的沸腾与圆管内存在很大差别,圆管内得出的ONB关系式不能直接用于棒束通道,但棒束通道内的沸腾曲线的趋势与圆管内的相似。
2) 实验测量结果与常用的Bergles等的关系式计算结果的误差较大。实验结果表明:在相同进口温度、流量、热流密度下,不同子通道内的ONB存在先后顺序,越靠近中心通道,沸腾点壁面过热度和热流密度越低,ONB的壁面过热度为2.1~5.6 ℃,与Basu等所得的结论基本一致。
3) 通过考虑棒束通道特殊的几何结构和热工参数对ONB的影响,根据实验数据拟合出棒束通道内ONB热流密度的新经验关系式,其预测值的相对误差为14.75%,与Bergles等的关系式相比,预测结果更加准确。
参考文献:
[1] MIZUTANI Y, TOMIYAMA A, HOSOKAWA S, et al. Two-phase flow patterns in a four by four rod bundle[J]. Journal of Nuclear Science and Technology, 2007, 44(6): 894-901.
[2] RIBATSKI G, THOME J R. Two-phase flow and heat transfer across horizontal tube bundles: A review[J]. Heat Transfer Engineering, 2007, 28(6): 508-524.
[3] HSU Y Y. On the size range of active nucleation cavities on a heating surface[J]. Journal of Heat Transfer, 1962, 84(3): 207-213.
[4] BERGLES A E, ROHSENOW W M. The determination of forced-convection surface boiling heat transfer[J]. Journal of Heat Transfer, 1964, 86(3): 365-372.
[5] 苏顺玉,王晓墨,黄素逸. 狭缝中流动沸腾传热过冷沸腾起始点的研究[J]. 热科学与技术,2004,3(2):104-107.
SU Shunyu, WANG Xiaomo, HUANG Suyi. Investigation of subcooled boiling incipience in flow boiling heat transfer through narrow channels[J]. Journal of Thermal Science and Technology, 2004, 3(2): 104-107(in Chinese).
[6] BASU N, WARRIER G R, DHIR V K. Onset of nucleate boiling and active nucleation site density during subcooled flow boiling[J]. Journal of Heat Transfer, 2002, 124(4): 717-728.
[7] 王甲强,贾斗南,郭赟,等. 环形窄通道内过冷沸腾起始点的实验研究[J]. 核动力工程,2004,25(4):319-323.
WANG Jiaqiang, JIA Dounan, GUO Yun, et al. Experiment study of the onset of nucleate boiling in narrow annular channel[J]. Nuclear Power Engineering, 2004, 25(4): 319-323(in Chinese).
[8] AHMADI R, UENO T, OKAWA T. Bubble dynamics at boiling incipience in subcooled upward flow boiling[J]. International Journal of Heat and Mass Transfer, 2012, 55(1): 488-497.
[9] AHMADI R, NOURI-BORUJERDI A, JAFARI J, et al. Experimental study of onset of subcooled annular flow boiling[J]. Progress in Nuclear Energy, 2009, 51(2): 361-365.
[10] BASU N, WARRIER G R, DHIR V K. Onset of nucleate boiling and active nucleation site density during subcooled flow boiling[J]. Journal of Heat Transfer, 2002, 124(4): 717-728.
