菱形微位移压电作动器的输入输出线性建模

张春林,张希农,陈杰,张帅

(西安交通大学机械结构强度与振动国家重点实验室, 710049, 西安)

菱形微位移压电作动器的输入输出线性建模

张春林,张希农,陈杰,张帅

(西安交通大学机械结构强度与振动国家重点实验室, 710049, 西安)

针对某定位装置的位移输出问题,研究了一种新型菱形微位移压电作动器,该压电作动器包括压电陶瓷、菱形微位移放大机构以及柔性铰链部分。对菱形微位移放大机构的放大系数进行了分析,发现该放大机构具有把压电堆的原始位移输出从30 μm放大到100 μm的能力,放大倍数与菱形环自身夹角θ有关,并且在压电堆输出范围内为比例放大,这些结果可以为更大放大系数的菱形环设计提供依据。建立了该菱形微位移压电作动器输入输出关系的理论线性模型,并将线性模型的模拟结果与实验结果进行了对比,证明该压电作动器线性模型具有较好的精度,能比较准确地反映微位移压电作动器的输入输出关系。

压电陶瓷;作动器;位移放大机构;线性建模

压电作动器因其输出位移分辨率高、出力大、响应快、功耗小等优点,已被广泛应用于机械、电力、航空航天等领域,是目前最具前途的智能驱动器件之一。但是,压电作动器的位移输出特性有时又限制了其在某些情况下的应用,因而在某些情况下压电作动器的应用需伴有位移放大机构[1]。国内外学者已对位移放大机构进行了大量的研究。国外的位移放大机构主要有杠杆机构[2-3]、Scott-Russell型位移放大机构[4]、钹型压电作动器[5]、放大尺式位移放大器[6]以及蜂窝杆式位移放大机构[7]等。国内关于位移放大机构的研究主要有:王隆太等对柔性铰链位移放大机构的研究[8];吴家龙等对液压微位移放大器的设计与研究[9];李万全等开展的基于液压微位移放大机构的压电陶瓷执行器的研究[10];等等。

本文提出的菱形微位移放大机构与钹型压电作动器[5]结构类似,但具有更紧凑的结构和更好的装配能力,同时还具有微位移特性、较大的放大系数以及能提供压电堆抵抗横向干扰力的能力。

建立作动器的输入输出模型对于整个作动放大机构的仿真、控制以及后续应用起着至关重要的作用,尤其是对于高精度的伺服控制[11]。为此,本文通过对菱形微位移放大机构的放大系数的分析,基于力学分析建立了位移放大器输入输出关系的线性模型,并通过实验对比验证了此线性模型的准确性,以期为菱形微位移压电作动器的后续应用提供理论参考。

1 菱形微位移压电作动器的原理

图1为菱形微位移压电作动器的示意图。该机构包含2部分:上部的柔性铰链部分(与目标装置相连);下部的菱形微位移放大机构,它给压电堆(PZT)提供约束,并主要实现位移放大功能以及与基底相连。当给压电堆一个输入电压时,压电堆将沿轴向输出一定的位移,同时菱形微位移放大机构会输出一个竖向位移,从而实现横向变竖向的位移放大。

图1 菱形微位移压电作动器示意图

2 线性模型

2.1 菱形微位移放大器的几何放大关系

菱形微位移放大机构为对称结构,可认为由8根杆件和8个柔性转角组成。本文假设8根杆件均为刚性结构,即忽略作动器在工作过程中杆件的弹性变形,则菱形微位移放大机构工作前、后的变形如图2所示,其中L1、L2分别为菱形框2条边的边长,ΔL和2H分别为输入和输出位移。定义Ra=2H/ΔL为放大系数。

图2 菱形微位移放大机构工作示意图

通过图2,可得到压电堆输入位移和菱形微位移放大机构放大后输出位移的关系式如下

(1)

整理后得

(2)

将式(2)关于ΔL作泰勒级数展开,可化为

(3)

式中:ΔL为压电堆的输入位移;2H为菱形微位移放大机构的输出位移;θ为初始状态时杆AB与水平压电堆之间的夹角;L1为杆AB的长度。当ΔL≪L1时,平方项中的ΔL/L1可认为是无穷小量,从而可得到式(3)的简化线性关系表达式

(4)

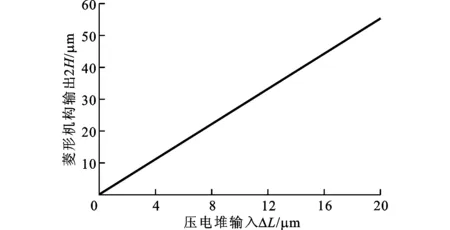
图3 菱形微位移放大机构的输入输出曲线

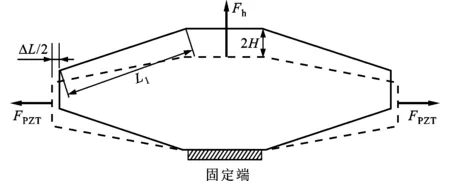
(a)菱形放大机构受力图

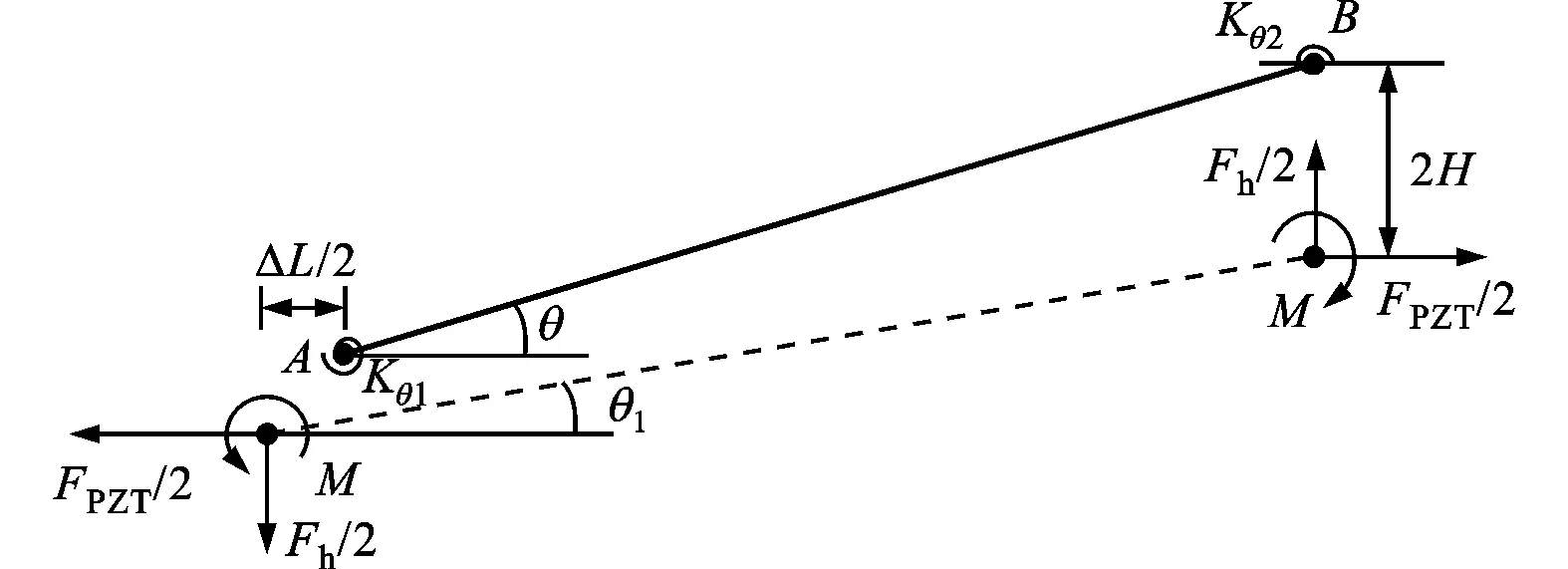
(b)1/4菱形放大机构变形图

2.2 菱形微位移放大机构输入输出线性模型

由于菱形微位移放大机构为对称结构,故取其1/4作为研究对象。图4为菱形微位移放大机构的受力示意图以及1/4放大机构的几何变形图。1/4菱形微位移放大机构被等效成刚体杆件AB和2个扭转弹簧。

当压电作动器无约束时,给作动器一个电压会产生一个大小为KvV的位移,其中V为电压,Kv为压电应变常数。当压电作动器有菱形环约束时,它将会提供给菱形环一个反作用力FPZT,同时柔性铰链也可能提供给菱形环一个竖直方向的外加力Fh,此时的受力如图4a所示。当取1/4位移放大机构为研究对象时,反作用力FPZT作用于A点可简化为力和力偶M的形式,受力如图4b所示,其中力偶

(5)

基于能量守恒原理,变形后外力所做的功等于A、B两点增加的势能,因此可以得到如下能量关系式

(6)

式中:Kθ1、Kθ2为A、B两点的扭转弹簧刚度系数;Δθ=θ-θ1。

由图4b,可得到变形前后的位移几何条件

(7)

式中:Ra为放大系数。

基于压电堆的本构关系,可得压电堆电、位移和力三者之间的关系为

(8)

式中:KP为压电堆等效刚度。

联立式(4)～式(6),可得菱形机构的线性模型

(9)

当菱形微位移作动器不给目标被驱动机构提供作动力(即Fh=0)时,式(7)可简化为

(10)

(Kθ1+Kθ2)的值可以由ANSYS静力分析求得。

基于ANSYS有限元软件,利用SOLID45三维实体单元建立了图4a所示菱形微位移放大机构的有限元模型。为模拟菱形微位移放大机构的实际工作受力情况,沿压电作动器(PZT)轴向(x轴方向)施加大小为154 N的对称面力。

图5为菱形微位移放大机构在上述载荷、约束下的变形图,图中的最大变形值(即图4a中的2H)为0.242 693 mm。由静力分析结果中力、变形的关系,可以求得式(8)中(Kθ1+Kθ2)的值。

式(8)最终可以简化为

2H=KV

(11)

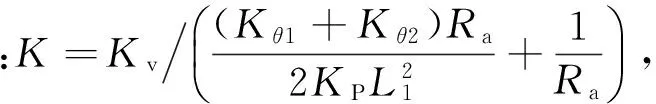
图5 菱形微位移放大机构静力变形图

3 压电作动器的输入输出测试实验

在微位移压电作动器中,使用的压电堆为Physik Instrumente P-885.91,正向饱和电压为120 V。因为压电陶瓷作动器不能承受大的拉伸载荷,而且其收缩驱动性能要显著弱于伸长驱动性能,所以为保证作动器安全稳定,取工作电压范围为0～120 V。图6为菱形微位移压电作动器实物图。实验系统包括:1台KEYENCE LK-G80激光位移计,测量精度为0.1 μm;1台预装Simulink的计算机;1套dSPACE 1103系统;1个西安交通大学自制的功率放大器。

图6 菱形微位移压电作动器实物图

图7为压电作动器输入输出测试实验的流程框图。首先由计算机生成一条线性的输入电压曲线,如图8所示。尽管压电堆能够施加一定量的负向电压,但为了系统稳定,仅允许系统的最低电压为0 V。计算机通过dSPACE系统把数字信号转化为电压信号,再经过功率放大器把该电压信号施加于微位移压电作动器,由激光位移计测量作动器的输出位移,并通过dSPACE系统把电信号转变为数字信号。图9为经过信号处理后所得到的压电作动器输出位移曲线。

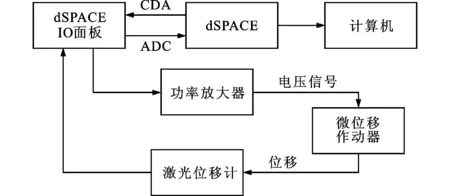
图7 压电作动器输入输出测试实验的流程框图

图8 压电作动器的输入电压曲线

图9 压电作动器的输出位移曲线

图10为位移放大机构输入输出关系线性模型的模拟结果与实验结果的对比图,可以看出:在电压上升阶段,线性模型的模拟结果与实验结果误差较小,能比较准确地反映微位移压电作动器的输入输出关系。

图10 线性模型模拟结果与实验结果的对比

4 结 论

本文针对某定位装置的位移输出问题,研制了一种新的菱形微位移放大机构。该放大机构具有把压电堆原始30 μm的位移输出放大成100 μm输出的能力。

由位移放大机构放大关系的分析可知,放大倍数与菱形环自身夹角θ有关,并且在压电堆输出范围内为比例放大,这一结论可为具有更大放大系数的菱形环设计提供依据。

菱形微位移压电作动器的位移输入输出测试实验结果表明,理论线性模型的模拟结果与实验结果相对误差较小,能比较准确地反映微位移压电作动器的输入输出关系,从而可为后续菱形微位移压电作动器的应用提供理论参考。

[1] XU W, KING T. Flexure hinges for piezoactuator displacement amplifiers: flexibility, accuracy, and stress considerations [J]. Precis Eng, 1996, 19(1): 4-10.

[2] OUYANG P R, ZHANG W J, GUPTA M M. A new compliant mechanical amplifier based on a symmetric five-bar topology [J]. J Mech Des, 2008, 130(10): 104501.

[3] ZUBIR M N M, SHIRINZADEH B. Development of a high precision flexure-based microgripper [J]. Precis Eng, 2009, 33(4): 362-370.

[4] TIAN Y, SHIRINZADEH B, ZHANG D. Development and dynamic modelling of a flexure-based Scott-Russell mechanism for nano-manipulation [J]. Mech Syst Signal Proc, 2009, 23(3): 957-978.

[5] JAMES F T, ROBERT E N. Special issue correspondence doubly resonant cymbal-type transducers [J]. IEEE Trans Ultrason, Ferro Elect, Freq Contr, 1997, 44(5): 1175-1177.

[6] ISHII Y, THUMME T, HORIE M. Dynamic characteristic of miniature molding pantograph mechanisms for surface mount systems [J] Microsyst Technol, 2005, 11(8/9/10): 991-996.

[7] MURAOKA M, SANADA S. Displacement amplifier for piezoelectric actuator based on honeycomb link mechanism [J] Sensors and Actuators: A Physical, 2010, 157: 84-90.

[8] 王隆太, 周志平, 马志新. 柔性铰链位移放大机构放大能力和负载能力分析 [J]. 机械设计, 2007, 24(7): 11-13. WANG Longtai, ZHOU Zhiping, MA Zhixin. Analysis on magnification ability and loading capacity of displacement magnification mechanism of flexible hinge [J]. Journal of Machine Design, 2007, 24(7): 11-13.

[9] 吴家龙, 李宝富, 张虎翼, 等. 液压微位移放大器的设计与研究 [J]. 机电一体化, 2010(5): 13-16, 20. WU Jialong, LI Baofu, ZHANG Huyi, et al. The design and analysis of hydraulic micro-displacement amplifier [J]. Mechatronics, 2010(5): 13-16, 20.

[10]李万全, 高长银, 冯地耘. 基于液压微位移放大机构的压电陶瓷执行器的设计 [J]. 机床与液压, 2011, 39(5): 88-89. LI Wanquan, GAO Changyin, FENG Diyun. Design on piezoelectric actuator based on hydraulic micro-displacement amplifying mechanism [J]. Machine Tool & Hydraulics, 2011, 39(5): 88-89.

[11]SHIN H C, CHOI S B. Position control of a two-link flexible manipulator featuring piezoelectric actuators and sensors [J]. Mechatronics, 2001, 11(6): 707-729.

(编辑 葛赵青)

LinearModelingforInput-OutputRelationsofaRhombicMicro-DisplacementPiezoelectricActuator

ZHANG Chunlin,ZHANG Xinong,CHEN Jie,ZHANG Shuai

(State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China)

A rhombic micro-displacement piezoelectric actuator (RMPA) is proposed to deal with the displacement output of a positioning device. The RMPA consists of three parts, i.e., a Pb based lanthanum doped zirconate titanate (PZT) actuator, a flexible hinge, and a rhombic amplification mechanism. The geometric amplification relations of amplification mechanism are analyzed. The mechanism can amplify the displacement output from 30 μm to 100 μm, and the magnification coefficient is proportionally magnified in a rated range and is related to the rhombic ring angleθ, which can provide a basis for design of rhombic amplification mechanism with greater magnification coefficient. A linear model of RMPA input and output relation is constructed, and the comparison between the linear model and experiments shows that the theoretical linear model has better expression for RMPA and higher accuracy.

Pb based lanthanum doped zirconate titanate (PZT); actuator; displacement amplifier; linearly modeling

10.7652/xjtuxb201405018

2013-11-05。 作者简介: 张春林(1988—),男,博士生;张希农(通信作者),男,教授,博士生导师。 基金项目: 国家自然科学基金资助项目(11102147)。

时间: 2014-03-05 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140305.1118.003.html

TP183

:A

:0253-987X(2014)05-0102-05