基于MATLAB的MAC序列相关特性仿真分析*
2014-08-08蔡凤丽刘新永
蔡凤丽,刘新永,徐 军
(1.安徽电子信息职业技术学院,安徽蚌埠233060;2.中国人民解放军装甲兵学院)
面对现代战争的海陆空一体化作战环境,军用雷达面临着种种威胁,雷达信号要求有理想的图钉形模糊函数,具有较高的测距、测精度、测速度以及良好的距离分辨能力.而雷达信号的许多特性是由二元PN伪随机序列码引起的,所以在雷达通信技术中PN伪随机序列码的选择直接影响雷达信号的性能.目前,Baker码序列和m序列是最常见的两种PN伪随机序列码,但这两种码序列长度都受限制,Baker码序列最长为13位,m序列的最长周期等于2n-1(n表示m序列生成器中移位寄存器个数),这两种常规的码序列由于长度有限,限制了它们的应用,文中主要介绍一种特殊的更适合现代雷达信号的码序列MAC(Multimode Arbitrary Code)序列,并基于MATLAB仿真软件对其相关特性进行仿真分析.
1 MAC码的生成算法
MAC码的长度是任意的,不受限制的,它是理想相关峰值PN伪随机序列码,抗遮挡能力比较强大.由MAC码调相的雷达信号实现方法简单,它的模糊函数类似图钉形.MAC序列具有较好的测距测速性能以及抗干扰能力.应用MAC序列设计雷达信号,可以根据应用的需要灵活选取对应的波形参数,满足雷达信号对诸多方面性能的高要求.
(1)生成任意长度的MAC码.可以采用以下方法产生MAC序列:假设MAC序列的长度,用l来表示,那么MAC码长l=p+u+v,用户可以设定(l≤1000),通过改变参数p、u、v来得到码长为l的不同MAC码序列.其中,参数p表示核心序列长度,取值应尽量大,核心序列L利用公式p=4t-1(t为整数)计算并从结果中取素数、参数u表示截取核心序列末尾u个元素、参数v表示截取核心序列开始v个元素.
(2)应用二次剩余算法产生MAC码.生成码长为l的MAC序列,采用的主要算法是:二次剩余算法.基本步骤为:首先确定素数p=4t-1,然后应用二次剩余算法得到核心序列(an,0≤n≤p-1),从得到的核心序列中截取末尾的u个元素,再截取核心序列前端的v个元素,将它们分别放在核心序列的前端和末尾,就可以产生长度为l=p+u+v的MAC序列{cn,0≤n≤n-1}.
应用二次剩余算法:
利用p=4t-1(t为整数)计算p值,从中取我们所需要的素数p,若(x2)p=i有解,则整数i为模p的二次剩余,否则i叫模p的二次非剩余.
按照以下步骤进行计算:
①计算
②当an=+1 时,查找i=1,2,…,p-1 数值,看其是否在①步骤中计算出的(p-1)/2个数中出现,如果出现,令ai=+1,否则ai=-1,可得核心序列L={a0,a1,…,ap-1},该核心序列的长度为p.
③从得到的核心序列L={a0,a1,…,ap-1}中截取末尾的u个元素,再截取核心序列L={a0,a1,…ap-1}前端的v个元素,将它们分别放在核心序列的前端和末尾,就可以产生长度为l=p+u+v的MAC 序列:{cn,0≤n≤l-1},即:
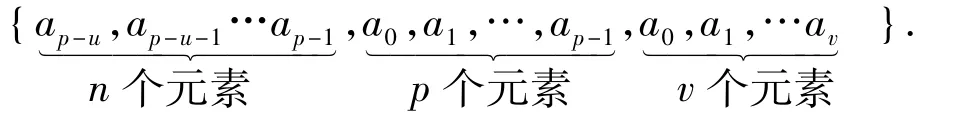
2 自相关函数分析
(1)核心序列和MAC序列的周期自相关函数.核心序列周期自相关函数,n=0,1,…,p-1,n=-1,-2,…,-(p-1) 对称.
MAC序列的周期自相关函数,n=0,1,…,l-1,n=-1,-2,…,-(l-1)对称.
(2)计算核心序列和MAC序列的非周期自相关函数.核心序列非周期自相关函数,n=0,1,…,p-1,n=-1,-2,…,-(p-1)对称.MAC序列的非周期自相关函数,,n=0,1,…,l-1,n=-1,-2,…,-(l-1)对称.
(3)计算MAC序列的互相关函数.序列{xn,0≤n≤l-1}和{yn,0≤n≤l-1}的互相关函数.
MAC序列具有良好的相关特性和任意长度.在MAC码序列的相关特性曲线中,只有两种数值(相关峰值为p,剩余的位置上全部是-1).假如MAC序列的长度相同,当p、u、v的数值选择不同时,峰值和位置也是不相同的.我们设计雷达信号的时候,调整u、v的大小不同,可以形成变化趋势尖锐的峰值,针对这种尖锐的峰值,选择合适的相关检测器,使目标从噪声中轻而易举检测出来.另外,对于被截断的部分回波信号,也可以得到良好的相关峰值.在设计通信系统时候,所选MAC序列,必须选的足够大,目的是为了对时域的不确定域进行覆盖.所以,针对不同的情况,应该设计选择合适的p、u、v数值,对于p、u、v数值的选择必须与实际应用相结合去考虑.
3 MATLAB仿真结果分析
3.1 基于MATLAB对已知某MAC序列进行相关特性仿真
当MAC序列已知时,编写相关特性仿真的Matlab仿真程序。

仿真结果如图1所示.

图1 程序中的MAC码序列相关性仿真图(88,5,17.6,8,11)
3.2 基于MATLAB对任意长度MAC序列码进行相关特性仿真
编写Matlab仿真程序:


其中,MAC序列可以取不同的长度,长度的数值可以在程序中修改.图2是基于MATLAB针对不同码长序列的MAC序列的周期自相关函数和非周期自相关函数的仿真图.

图2a 仿真结果1(l=100,ans=31.0000)

图2b 仿真结果2(l=600,ans=499.0000)

图2c 仿真结果3(l=800,ans=683.0000)
图2几种MAC序列的周期自相关和非周期自相关特性仿真结果,括号中的数字为(MAC序列码长,主旁瓣比)
4 结束语
综合图1和图2的仿真结果可以得出以下结论,对已知的MAC序列来说,由于长度是固定不变的,当初始状态不同的时候,MAC码序列的码元排列也是不一样的,对应自相关函数的主旁瓣比不同.综合图2的三幅仿真图,可以看出,MAC序列是一种典型的PN伪随机序列码,是具有良好相关特性的序列,从对周期自相关与非周期自相关特性的仿真情况来看,MAC序列的周期自相关特性非常好,但是MAC序列的非周期相关特性却不如想象中的那么优良.结合图2中的a、b、c三幅仿真图得出结论,随着MAC序列码的长度数值逐渐增长(即码长增长),相对应的主旁瓣比越来越大,相关特性越来越好,所以,MAC序列的非周期自相关特性虽然没有Baker和m的理想,但是利用MAC码这种PN伪随机序列码所设计的雷达信号在接收端进行相关检测的时候,非常容易就被相关检测器检测出来.通过本文的研究可见,MAC序列具有良好的相关特性,MATLAB在电子、通信、军事雷达等技术中,是一种很好的仿真应用工具.MATLAB仿真软件在仿真过程中充分发挥了软件本身的强大功能.
[1]M.I.斯科尔尼克,林茂庸,穆云明,毛二可.雷达系统导论[M].北京:国防工业出版社,1992.
[2]杨文华,宋力平,王其扬.巴克码的旁瓣抑制[J].上海航天,1996(4).
[3]张登银,等.MAC序列码雷达信号设计[J].电子与信息学报,2003,25(12).
[4]杨立扬,等.基于MAC序列的间断连续波雷达信号的研究[J].电子学报,2004,32(6).
[5]何国胤,等.一种特殊序列在间断连续波雷达中的应用[J].指挥技术学院学报,2001,12(3).
[6]杰里·L·伊伏斯,爱德华·K·里迪.现代雷达原理[M].北京:电子工业出版社,1991.
[7]张群逸.雷达中的相位编码信号与处理[J].火控雷达技术,2005,34(12).
