基于调速法交叉航路冲突调配时机分析
2014-08-07赵嶷飞王红勇
赵嶷飞,陈 琳,王红勇
(中国民航大学 天津市空管运行规划与安全技术重点实验室,天津 300300)
基于调速法交叉航路冲突调配时机分析
赵嶷飞*,陈 琳,王红勇
(中国民航大学 天津市空管运行规划与安全技术重点实验室,天津 300300)
以在相同高度层、交叉航路飞行的两航空器为研究对象,应用运动学知识建立航空器运动轨迹随时间变化方程,判断任意时刻两机间距离与标准安全间隔关系,预测飞行冲突.采用影子调速方法,对一架航空器调速,以调速值最小为目标函数,建立冲突调配模型,确定其最迟调配时间点;在此基础上,构建交叉航路夹角与最迟调配时间点函数关系,得出“交叉航路为锐角且速度调整值一定时,最迟调配时间随航路夹角的增加而减小”这一结论.最后以飞往大王庄台的 A593 和 A461 两航路航班为例,进行仿真,输出了调速值、调配时机与航路夹角间三者关系曲线,该曲线可为扇区内航路规划提供参考,并验证上述结论的准确性.
航空运输;最迟调配时机;调配门限;交叉航路
1 引 言
近年来,随着我国低空空域改革政策的提出及通用航空产业的发展,空中交通流量持续上涨,在一定程度上增加了航空器运行过程中的潜在冲突风险.尽管空管新技术发展显著,应用先进的通信、导航、监视(CNS)技术对航空器在整个飞行过程中实施监控、识别和引导,很大程度上保障了空中飞行的安全性和有序性.但不可否认,愈加开放和复杂的航行环境对维持和提高空中交通管理系统安全性、灵活性、可预测性等提出了更为严格的要求.因而,为保障空中交通运行安全,针对不同航路的构型及布局,分析其飞行过程中可能的潜在冲突,并给出相应的调配方案具有一定研究价值.
实际管制过程中,对于冲突的调配主要采用改变飞行高度、飞行速度和飞行航向三种方式;其中,飞行高度的改变可以将冲突快速有效化解,但在爬升、穿越过程中易对周边航空器运行产生干扰.调速在实施过程中同样较为便捷,优势在于干扰较小.从理论层面,国内外学者对冲突调配的主要研究成果有:将免疫遗传[1-4]等智能算法应用于冲突解脱;研究多 Agent 的冲突解脱算法[5];采用动态优化[6]、混合整数规划[7]、最优控制理论[8]等数学方法,确定调速区间,研究冲突避让与调速值间关系;从低空空域角度,研究飞行冲突避让的改航及调速算法[9];国外学者 Tomlin 等应用了非合作博弈理论,得出最优控制规则,并采用预先设定的冲突解决策略[10];Ghosh 采用电势能法研究冲突解脱方案,该方法难以实时计算,且得出的冲突调配方案并非总是最优[11].上述算法从理论上能够对冲突进行调配,但较少考虑航线结构对于调配的影响,对于何时进行调配,调配时机与航路间结构关系没有进行深入讨论,在实际应用中有一定的局限性.
本文以交叉航路为研究对象,根据运动学方程分析相同高度层飞行的两飞机随时间变化轨迹,对比圆形保护区两圆圆心间距离与水平间隔标准间关系,判断飞行冲突.采用影子调速方法对其中一架航空器调速,根据调速值确定最迟调配时间点,构建冲突调配模型,分析了交叉航路夹角与最迟调配时间点间函数关系.最后应用 matlab,选取飞往大王庄台的 A593 及 A461 航路的两架飞机进行仿真,输出调速值与最迟调配时间点间关系曲线,在此基础上,通过改变航路夹角,分析交叉航路夹角、调速值与最迟调配时间点三者函数关系.
2 基于调速法的冲突调配
2.1 问题简化
对飞行在同一高度层交叉航线上的两飞机而言,假定:
(1)飞机模拟成一个有方向的质点,运动方向就是飞机的飞行航向[12];
(2)设飞机在交叉航路沿航线匀速飞行,不考虑任何偏差[13];
(3)飞行过程中不考虑沿航迹误差,垂直航迹误差及风向、风速等随机因素;
(4)飞机调速过程瞬间完成;且只改变速度大小,不改变飞行航向.
在此基础上,本文对于该问题基本研究思路如图1所示.
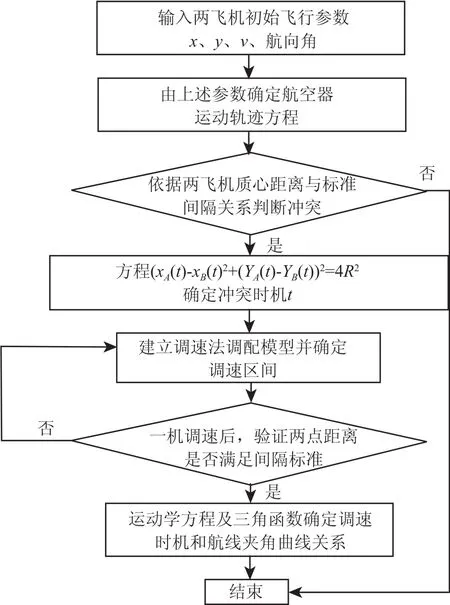
图1 流程图Fig.1 Flow diagram
2.2 基于距离标准的冲突探测
冲突探测是根据地面监视设备对飞机在空域中的位置和速度信息进行计算,判断飞机是否会与其他飞机相撞或小于最小间隔标准[14].分别对飞机建立相应保护区,如果一架飞机进入另一架飞机的保护区,即认为存有飞行冲突.本文以处于相同高度层、交叉航路飞行的两机为研究对象,根据飞行航迹计算两机间最小距离 Dmin,将 Dmin同安全间隔标准作比较,判断冲突是否发生.
设两架飞机分别为 A、B,已知飞行基本参数(X0(i),Y0(i),V(i),θ(i)),依次 为初始横、 纵坐标,初始速度,航向角.任意时刻两机坐标可表示为A(XA(t),YA(t)),B(XB(t),YB(t)).

目前,空中交通管制规则中规定飞行安全的间隔标准距离 d=10 km,可知:
(1) 当 Dmin≤ d,有冲突发生;
(2) 当 Dmin> d,无冲突发生.
通过该方法,一方面可以确定是否有冲突发生,另一方面可以确定冲突时刻,为调配时机的选择奠定基础.
2.3 调速法冲突调配模型
当判定出两机在 t时刻存有潜在冲突,通过对飞机提前调速的方法,使得调速后两机在 t时刻满足最小间隔标准.依据影子调速模型确定调速区间,并根据调速值 ΔVi确定最迟调配时间点,构建冲突调配模型.
2.3.1 影子调速模型[7]
定义 ΔVi为任意一架飞机速度变化量,选定某种机型后,飞机飞行速度的上下界随之确定,调速之后需满足:Vmin≤ V+ ΔV ≤ Vmax.基于两机间相对位置关系建立 ΔVi的约束条件,确定飞机调速区间 [ai,bi].
已知两架飞机飞行基本参数 (X0(i),Y0(i), V(i),θ(i)), ΔVA、 ΔVB为速度调整值;得任意时刻飞 机A、B速度矢量差为VA- VB=作两条平行于矢量 VA-VB且与飞机 B 圆形保护区相切的直线,称其为飞机 B 沿飞机 A运动方向的影子.可知当飞机A的保护区与飞机B的影子有交集时,会有冲突发生.如图2 所示.
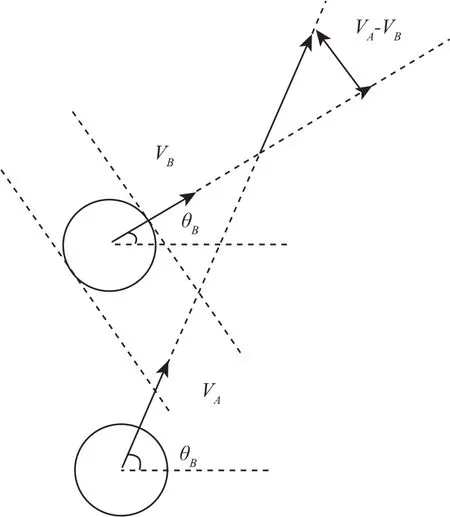
图2 冲突调配限制条件Fig.2 Conflict adjustment limit condition

图3 飞机 B影子与飞机 A保护区相切Fig.3 Shadow of aircraft B tangent with aircraft A protected area
由图3知:①飞机 B 影子相切于飞机 A保护区右侧,设影子与水平轴夹角为 L12,根据图2 原理,若飞机 B 影子与水平轴夹角大于 L12,无冲突.②飞机B影子左切飞机 A保护区,若飞机 B 影子与水平轴夹角大于 α12(影子与水平轴夹角),无冲突.
设两机距离 D12, δ12为两机连线与水平轴夹角,β为两圆心与两圆公切线夹角,则有
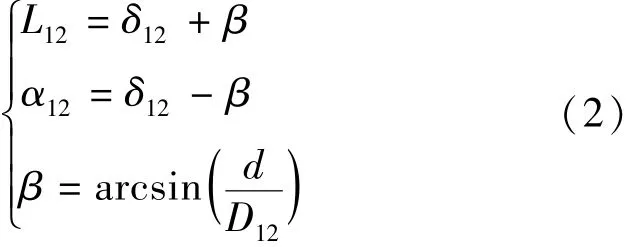
速度矢量差与水平轴夹角设为 θ12,则有

综上得出:两机间无冲突,需满足

将式(4)与飞机调速范围约束条件 Vmin≤ V+ ΔV≤ Vmax结合,求出飞机调速区间为 ΔVi⊂ [ai, bi],i=1,2,…,n,考虑到燃油成本、乘客舒适度等因素,取调速区间最小值 ΔV 为目标函数.
得出基本调速模型为

2.3.2 确定最迟调配时间点

图4 调配距离图Fig.4 Adjustment distance diagram
交叉航路两机飞行相遇如图4 所示.两机 A、B分别从 A0、B0飞行,飞行 t时间至 A1、B1时发生冲突;t前某点 Δt对 A 机进行调速,使得 t时飞行至A2点,与 B 冲突解脱.以一机调速、一机恒速为例,进行讨论.设 A 机调速区间 ΔVi⊂ [ai,bi],图中 S点为调速值ΔVA下对应最迟调速时间点,其物理意义为:S 点改变 A 机飞行速度为 VA+ ΔVA,满足SA0段及 SO 段飞行与 B 机距离满足间隔水平标准,且航段 SA0(提前调配距离)最长.
已知两机 A、B 基本飞行要素,最迟调配时间点i确定步骤如下:
(1)i=1,即 A 机从第一点调速,速度变为 VA+ ΔVA;满足
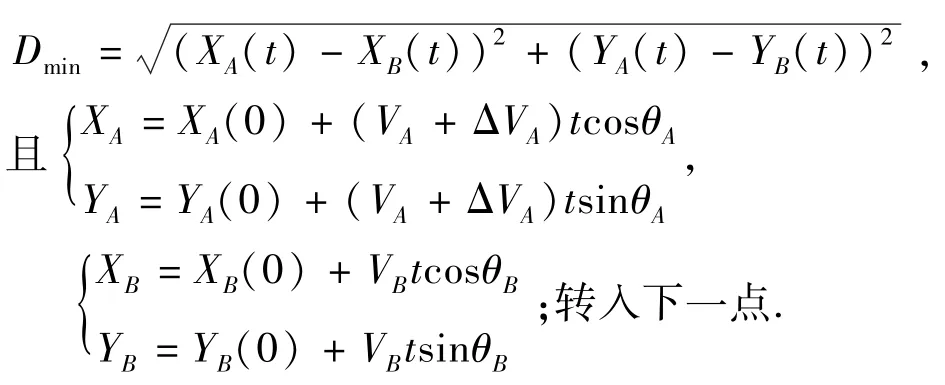
(2)搜索至 i时,A 机速度由 VA变为 VA+ ΔVA, 且 j=i+1;满足

(3)i=j时,转入 j搜索,假设不满足上述条件,则跳出循环;i点即为最迟调配时机点.
2.4 最迟调配时间点与航路夹角关系研究
假设飞行相同时间 t,A 机根据调速值 ΔVA及对应最迟调配时间点飞行,位置点变为:

即图4 中 A2点,飞机 B 位置点不变,仍为图中B1,此时两机相对位置关系如图4 中连线 A2B1所示.
设两航路夹角为γ,通过航迹位置点坐标及三角函数关系,对 ΔOA2B1应用余弦定理,可得


将式(11)带入式(10),可构建出最迟调配时间点、调速值以及航路夹角间函数关系,即 Δt= f(γ,ΔVA),根据仿真验证.
3 算例分析
为保证调配模型及其与航路夹角关系在实际运行环境中的可用性,选择一个交通繁忙区域,采集 ADS-B 数据进行评估验证.研究对象:以飞向大王庄台的 A593 和 A461 的航路航班为例,对一机调速,确定最迟调配时间点.
航班选取过程:根据大王庄台、衡水台、泊头台、经纬度信息及接收 ADS-B 数据中显示的经纬度,选取与上述导航台位置相对较近航班,通过经纬度与 X、Y 坐标间转化,得到两航班初始位置点坐标,航向、飞行速度同样通过 ADS-B 数据读取.
设:A 为大王庄台和衡水台之间一航班,VA= 186 m/s, 航向角θA=182°, 初始点(1 456 868, -237 322).B 为大王庄台与泊头台间一航班,VB= 165 m/s,航向角 θB=187°,初始点 (1 472 068.4, -235 257.1),进场飞行高度一般为 4800-5 400 m.选取 A、B 机型均为 B737-300,速度范围:设定以最小光洁速度 389 km/h(108 m/s) 为下限;最大巡航速度 829 km/h(230 m/s) 为上限.( 由于不同航空公司特定飞行高度下速度区间各不相同,选取一天 ADS-B 数据,读取速度信息,基本符合上述划设区间)
根据任意时刻点两机位置坐标与式(1),利用 matlab 进行仿真,得出在 t=200 s 时,两机间相对距离最短,且小于安全间隔标准.如图5 所示,相对飞行的航空器对间两圆形保护区距离迅速减小,达到最小值后又迅速增大 ,反映了相对飞行在冲突之前迅速接近,冲突之后又快速分开的过程.

图5 两机距离随时间变化曲线Fig.5 Distance time diagram

图6 冲突演变过程Fig.6 Conflict change process diagram
图6详细介绍了冲突发生阶段两圆相对距离的变化过程,其中,t1=200 s 时,D1=9 250 m<d,为冲突初始发生时刻,t2=294 s,两机间冲突解脱,相对距离大于安全间隔.由此可见,相对冲突具有迫近率大这一特点,具有较高安全风险,应及时采取调配方案进行冲突解脱.采用调速法调配方案为,对飞机 A 进行调速,B 机保持不变.由式(2),算得β12=37o, δ12=7o,带入式(3)、式(4),联立解方程组.求得飞机 A 调速区间为 ΔVA⊂ [-72 m/s,-2 m/s].
根据调配模型目标函数,取 ΔVA=-2 m/s,进行计算.调速后 VA+ ΔVA=184 m/s,VB=165 m/s,通过 matlab 仿真计算,验证当 A 进行调速后,任意时刻 A、B 机相对位置满足安全间隔标准.结果如图7所示.
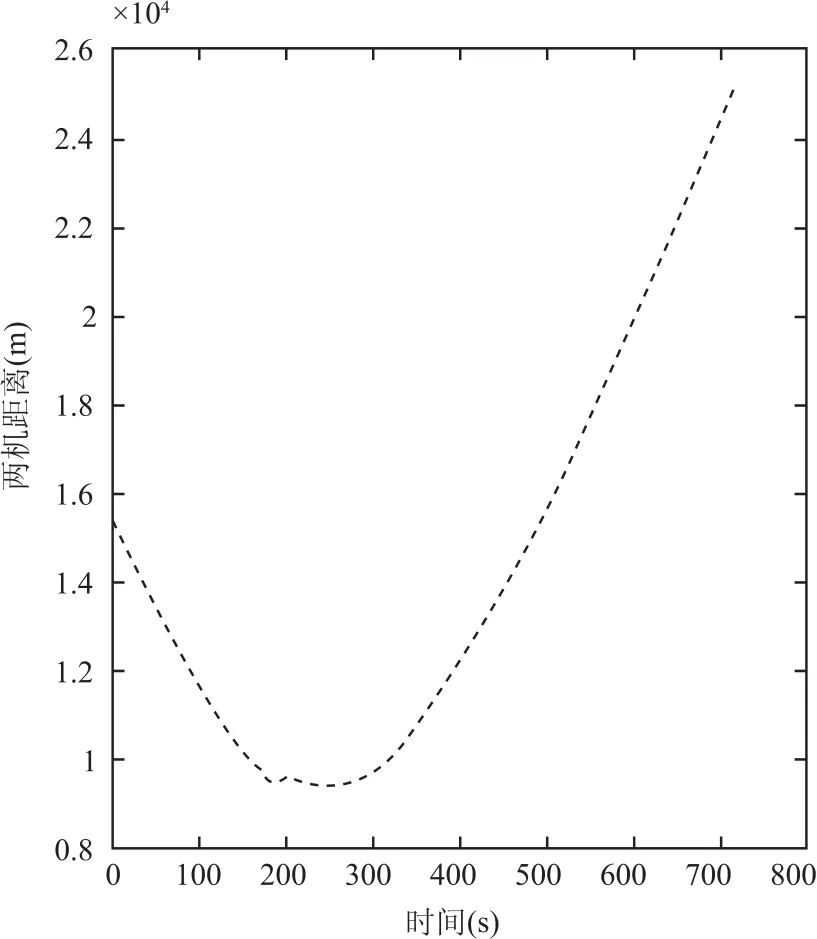
图7 调速后两机相对距离随时间变化曲线Fig.7 Distance time diagram after speed adjustment

确定调速值后,根据搜索方法可确定其最迟调配时间点. 当调速值 ΔVA在调速区间 [-72 m/s, -2 m/s] 取任意值,对应的最迟调配时间点发生变化,如图8 所示,得出“随调速值(绝对值)的减小,最迟调配时间点提前”这一结论.
上述分析是基于交叉航路夹角不变( γ =50)情况下的仿真结果.现在分析当夹角变化时(γ = 50,100,150),最迟调配时间点、调速值、夹角三者关系.假定航空器飞行过程始终为按既定航向飞行这一理想状态,根据两机航向即可确定交叉航路夹角.为引入航路夹角这一变量,采用改变 B 机飞行航向的方法来更改航路夹角,但根据几何关系保证“B机距交叉航路交点距离不变且两机初始速度差不变” 这一条件,在调速区间[-72 m/s,-2 m/s] 内取不同调速值,研究调速值、最迟调配时间点与航路夹角三者函数关系.仿真结果如图9所示.
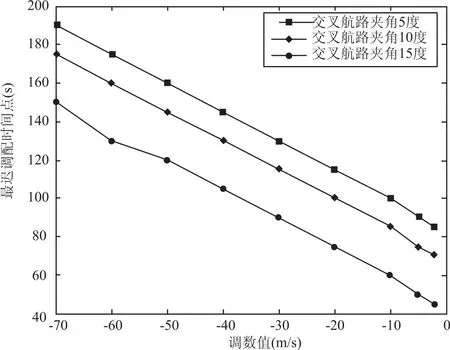
图9 不同调速值、最迟调配时间点与航路夹角关系曲线Fig.9 Different speed adjustment value latest adjustment time with intersection airway angle diagram
讨论:
(1)相同航路夹角情况下,最迟调配时间点随调速值(绝对值)的增大而推后.即速度变化量越小,相同时间内,提前调速距离线段 SA1越小.
(2)速度调整值一定情况下,即(VA+ ΔV)一定时,最迟调配时间点随航路夹角的增加而增大.表明,当航路夹角较小时,需提前对冲突进行调配;航路夹角较大时,冲突调配可稍晚进行.
(3)最迟调配时间点一定时,航路夹角越小,速度减小值越大.表明:航路夹角较大时,通过较小的速度改变量就可将冲突合理解脱;夹角较小时,情况相反.
4 研究结论
本文基于调速法冲突解脱模型,计算调速区间,确定最迟调配时间点.重点探讨了航线结构对于调配时机的影响.通过实例仿真,得出“相同航路夹角情况下,最迟调配时间点随调速值(绝对值)的增大而推后”这一结论.并在此基础上,研究航路夹角、最迟调配时间点及调速值三者间关系曲线.但在分析过程中,将飞机模拟成带方向的质点且匀速飞行,没有考虑沿航迹、垂直航迹误差及一些随机因素,与实际情况在一定程度上有所偏差.
[1] 杨尚文,戴福青.基于一种免疫遗传算法的自由飞行冲突解脱[J].航空计算技术,2007,37(1):41-43.[YANG S W,DAI F Q.Conflict resolution in free flight based on an immune genetic algorithm[J]. Aeronautical Computing Technique,2007,37(1): 41-43.]
[2] 吴君,张京娟. 采用遗传算法的多机自由飞行冲突解脱策略[J].智能系统学报,2013,8(1):1-5.[WU J,ZHANG J J.Conflict resolution of multiple airplanes in free flight based on the genetic algorithm[J].CAAI Transaction on Intelligent System,2013,8(1):1-5.]
[3] 郭茜,聂润兔,王超.蚁群算法在解决空中交通飞行冲突中的应用[J].交通运输工程与信息学报, 2009,7(2):116-119.[GUO Q,NIE R T,WANG C. Application of ant colony algorithm to aircraft conflict resolution[J].Journal of Transportation Engineering and Information,2009,7(2):116-119.]
[4] 刘星,胡明华,董襄宁.遗传算法在飞行冲突探测解脱中的应用[J].南京航空航天大学学报,2002,34 (1):36-39.[LIU X,HU M H,DONG X N. Application of genetic algorithms for solving flight conflicts[J].JournalofNanjing University of Aeronautics&Astronautics,2002,34(1):36-39.]
[5] 戴玲,夏学知.多 Agent技术在飞行冲突解脱中的应用[J]. 舰船电子工程,2008,28(3):62-64.[DA I L,XIA X Z.Application of multi-agent in flight conflict resolution[J].Ship Electronic Eng.,2008, 28(3):62-64.]
[6] Raghunathan U,Gopal V,Subramanian D.3D conflict resolution of multiple aircraft via dynamic optimization [C ] ∥ AIAA 2003-5675, AIAA Guidance, Navigation,and Control Conference.Austin:AIAA, 2003:1-18.
[7] Lucia Pallottino,Eric M.Feron,Antonio Bicchi. Conflict resolution problems for air traffic management systems solved with mixed integer programming[J]. IEEE Trabsaction on Intelligent Transpotation Systems, 2002,3(2):3-11.
[8] 程丽媛,韩松臣,刘星.采用内点约束的最优冲突解脱方法[J].交通运输工程学报,2005,5(2):80-84. [CHENG L Y,HAN S C,LIU X.Optimal conflict resolution method based on inner-point restriction[J]. Journal of Traffic and Transportation Engineering, 2005,5(2):80-84.]
[9] 朱代武. 低空空域飞行冲突避让算法[J]. 交通运输工程 学 报,2005,5(3):73-76.[ZHU D W. Calculational methods of avoiding flight conflict in low altitude airspace [ J]. JournalofTraffic and Transportation Engineering,2005,5(3):73-76.]
[10] C Tomlin,G Pappas,S Sastry.Conflict resolution for air traffic managent:A study in multi-agent hybrid systems[J].IEEE Transactions on Automatic Control, 1998,43(4),509-521.
[11] Ronojoy Ghosh,Claire Tomlin.Maneuver design for multiple aircraft conflict resolution proceedings of the American control[C].Conference Chicago,Illinois. 2000,3(2):672-676.
[12] 徐肖豪,李冬宾,李雄.飞行间隔安全评估研究[J].航空学报,2008,29(6):1411-1417[XU X H,LI D B,LI X.Research on safety assessment of flight separation[J].ACTA Aeronautica ET Astronautica Sinica,2008,29(6):1411-1417.]
[13] 赵洪元. 两条交叉航线上飞机发生危险冲突次数模型的研究[J].系统工程与电子技术,1998(5):6-9. [ZHAO H Y.Study on the model for computing the number of dangerous conflicts among aircrafts on two intersecting tracks[J].Journal of System Engineering and Electronic,1998(5):6-9.]
[14] 刘星,韩松臣. 用于自由飞行冲突探测的 Delaunay方法[J].数据采集与处理,2002,17(4):446-449. [LIU X,HAN S C.Delaunay method for free flight conflict detection[J].Journal of Data Acquisition& Processing,2002,17(4):446-449.]
Intersection Airways Conflict Adjustment Time Based on Speed Adjustment Method
ZHAO Yi-fei,CHEN Lin,WANG Hong-yong
(Tianjin Key Laboratory for Air Traffic Operation Planning and Safety Technology, Civil Aviation University of China,Tianjin 300300,China)
The research object of this paper is aircrafts which fly on the same flight level of intersection airways.In order to judge the relationship between distance of two aircrafts and standard flight separation,it considers kinematic equations which change with time to build aircraft flight trajectory equation and predicts flight conflict.Based on the method of speed adjustment of one aircraft,which develops a model of conflict resolution,regarding the value of minimum speed as objective function and determine the latest adjustment time.Then,the thesis analyses the function between the cross track angle and latest speed adjustment time, gets the conclusion that “ Speed adjustment value under certain circumstances,when intersection airway angle increase,the ahead adjustment distance decrease.” Finally,choosing the flights which fly on A593 and A461 as example,making a simulation and considering the relation curve of latest adjustment time change with route angle and speed adjustment value.This result provides the reference for the airways planning,also proves the correct of the forward conclusion.
air transportation;latest adjustment time;adjustment threshold;intersection airways
1009-6744(2014)01-0095-07
U268.6
A
2013-06-04
2013-08-26录用日期:2013-10-12
国家科技支撑计划(2011BAH24B10);国家自然科学基金 (61039001);中央高校基本科研业务费(ZXH2012M001);国家自然科学基金委员会与中国民用航空局联合资助项目(U1333108);民航局项目 (MHRD201018).
赵嶷飞(1971-),男,湖南常德人,博士,教授.
yifei6666@sina.com
