加速列生成法求解乘务调度问题

陈仕军,沈吟东

(华中科技大学 自动化学院,武汉 430074)

加速列生成法求解乘务调度问题

陈仕军,沈吟东*

(华中科技大学 自动化学院,武汉 430074)

列生成法是求解乘务调度问题的有效数学规划方法,但传统列生成法存在收敛速度慢的缺点.基于乘务问题特点,提出三种加速列生成求解的策略:在列生成迭代过程中,每隔一定周期移除受限主问题的部分“差”变量,以减小问题规模;提出基于乘务问题特征的强标号消除准则和基于该准则的二阶段子问题求解法以加速子问题求解;利用分支树求解整数解时,提出一个能充分利用已有解信息的班次池策略,以减小整数解求解时间.利用实际公共交通中的 10 组案例对所提加速策略进行测试.实验结果表明,这些加速策略能够有效加速列生成的求解,适用于求解大规模的乘务调度问题.

系统工程;列生成法;加速策略;乘务调度;问题特征

1 引 言

乘务调度问题是公交企业普遍面对的重要问题,也是计算科学界的 NP 难题.有效的调度方法能提高管理效率,并节约大量的人力成本.从上世纪60年代开始,众多学者和交通领域专家对该问题进行了深入研究,提出了各种有效的优化模型和解决方法[1].

列生成方法是求解大规模线性规划问题(LP)的有效方法,它通常与分支定界方法结合,用于解决大规模整数规划问题(ILP)[2].该方法也被广泛用于求解各类交通领域(公共交通、铁路、航空等)的乘务调度问题[3,4].对于某些大规模 LP 问题( 称主问题,记作 MP),其变量数可能太多以至于难于直接求解整个 LP 问题.此时,列生成方法显示出其优越性.其主要过程是:求解时只考虑分部分变量集上的 LP 问题(称受限主问题,记作 RMP);求解后,根据其对偶乘子信息求解一个子问题(SP),以期得到能改进目标值的新变量(列);将新列加入 RMP 以扩大其规模,再求解新的 RMP 问题.以上过程重复进行,直到没有改进 RMP 的新列为止.尽管列生成法已被应用于解决多种大规模 ILP,但仍然存在不稳定、收敛速度慢的缺点[2].

由列生成法的求解过程可知,列生成法的效率主要由两方面决定:RMP 问题的求解速度与 SP 问题的求解速度.目前,部分文献针对各种不同具体问题,从不同侧面提出了一些改进列生成效率的方法.例如,Gondzio[5]提出一种原始对偶内点方法用于加速求解 RMP 的近似解.Elhallaoui 等[6]提出一个动态约束集结方法,来减小 RMP 的退化程度以加快其收敛速度.由于乘务调度的子问题等价于带资源约束的最短路问题 (RCSPP),是 NP 难题,部分学者对 RCSPP 求解提出一些改进方法,例如双向动态定界法[7]、状态空间松弛法[8]等,并用于求解车辆路径问题. 此外,Leitner 等[9]、 Alves 与 De Carvalho[10]基于问题特征,研究了对偶乘子稳定性方法以加速列生成法的收敛速度,分别用于解决网络设计和变尺度装箱问题.上述加速求解方法都需要结合具体问题特征,难以直接应用于解决乘务调度问题.本文基于乘务问题特点,从主问题、子问题及整数解求解等方面,提出了三种加速策略用于解决乘务调度问题.

首先,在传统列生成方法中,RMP 的规模在持续增大.当 RMP 增大到一定规模后,其求解会花费较长时间.为此,本文设计了一个“差”(无助于改进目标值)变量移除策略来降低 RMP 的增长规模,并加速列生成求解.其次,在求解子问题时,需要利用多标号动态规划方法求解 RCSPP.为了提高求解效率,一般采用标号消除准则消除部分标号,只保留帕累托(Pareto) 最优标号集[11].注意到实际中 Pareto 最优解仍然包含大量标号(特别是当网络和资源集规模较大时),且很多标号不会成为最优解.为此,本文基于乘务问题特点,提出一种新的强标号消除准则,并基于此提出一个二阶段子问题求解方法,以提高子问题求解效率.最后,利用分支定界方法求解整数解时,需要在每个节点利用列生成法计算其相应 LP 解.因此,子问题对应的RCSPP 求解也要在整个分支树进行,使得整数解求解花费太多时间.本文考虑在搜索整个分支树时,充分利用已有解信息,提出一种班次池策略:即为每个节点设计一个班次池用于继承其父节点已生成的既有班次.在求解子节点的子问题时,优先考虑其班次池中的班次,只有当班次池中没有班次能改进目标值时才调用 RCSPP 以生成新班次.该方法能减少子问题的求解时间,从而能缩小整数解的求解时间.

2 乘务调度模型

乘务调度问题可描述为[12,13]:在满足各种劳动法规约束下,合理安排乘务员去执行所有给定的车辆任务,并使得所用乘务员数量最少或总工时成本最小.

一般,乘务调度可以用集覆盖模型来表示.记最小值乘段集合 M={1,2,…,m},所有可行班次集合 N={1,2,…,n},班次 j∈ N 的成本 cj.对于∀i∈ M 和 ∀j∈ N, 若班次 j包含 i,则记 aij=1;否则记 aij=0.对于 ∀j∈ N,定义决策变量 xj如下:xj=1 表示班次 j被选择,否则 xj=0.则乘务调度模型可描述为

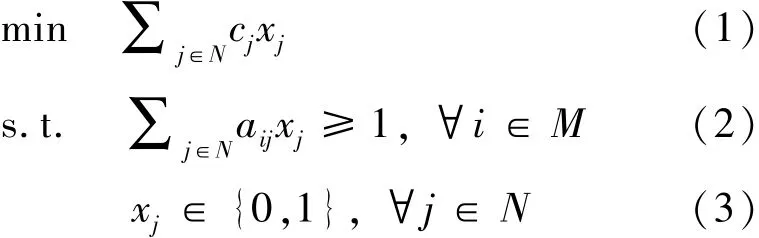
目标函数(1)是最小化总成本;约束(2)表明每个最小值乘段至少被一个乘务班次所覆盖;约束

(3)是0-1 决策变量.

3 基于列生成法的乘务调度问题求解

3.1 基本的列生成算法

列生成算法主要用于求解 ILP 的线性松弛问题(称为主问题,记做 MP),以得到 ILP 的下界.其主要是通过迭代求解一系列的受限主问题(RMP)和子问题(SP),最终收敛到最优解.其中,RMP 对应部分变量(列或班次)集上的线性松弛问题,SP在于生成能改进 RMP 目标函数值的新班次.记第 r次迭代时,受限主问题为 RMPr,子问题为 SPr.记 RMPr对应的部分变量集,则 RMPr为如下优化问题:

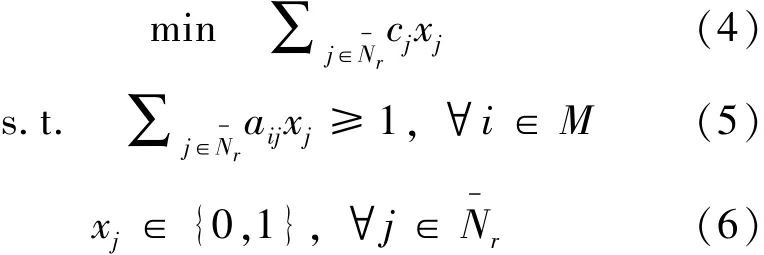
由于 RMPr只考虑了部分变量集以外仍可能有改进目标值的变量.根据线性规划单纯型原理,能改进目标值的变量是具有负判别数的变量.记约束(5)对应的对偶乘子向量为, 则对于 ∀j∈ N,其判别数 rcj计算如下:

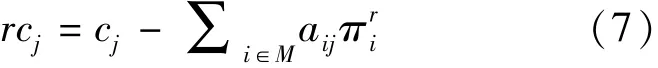
为了判断 N-r以外是否具有负判别数的变量,需要求解具有最小负判别数的变量.因此,子问题SPr为如下优化问题:式(8)中,Pr返回具有最小负判别数的变量集.

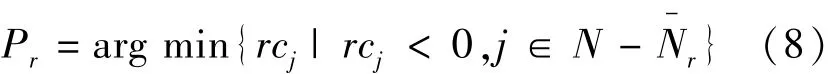
有了上述定义,列生成算法求解乘务调度问题的基本步骤如下:

Step1r ← 0,构造初始列集,形成初始受限主问题 RMP0;

Step2求解受限主问题 RMPr,得到约束(5)对应的对偶乘子向量 πr;

Step3求解子问题 SPr,以得到改进 RMPr目标值的班次集 Pr;

Step4若 Pr= ∅ ,则已经求得 MP 的最优解,转 Step6;

Step5将新班次集 Pr加入到 RMPr,即

Step6若 MP 最优解是整数解,则停止;

Step7对当前节点分支,用分支定界方法求解整数解.

在 Step1 中,通过设置人工变量方法构造初始列集,从而形成初始 RMP0.由于新生成的班次需要满足多种班次合法性约束,因此 Step3 中的子问题 SPr等价于带资源约束的最短路问题(RCSPP),需要利用多标号动态规划方法求解[11].最后,Step7中利用基于换班机会(RO)的分支策略求整数解,具体参见 3.3 节.

3.2 三种列生成法的加速策略

本文基于乘务问题特点从主问题求解、子问题求解及整数解等方面,提出了三种列生成的加速求解策略.

(1)列移除策略.

基本列生成算法中,RMPr的规模随迭代次数 r在不断增大,其求解速度会逐渐变慢(特别是对大规模问题).为了限制 RMPr的增长规模,考虑迭代求解过程中移除 RMPr中较“差” (无助于改进RMPr目标值) 的变量集,从而加快求解 RMPr速度.根据线性规划单纯型原理,具有负判别数的变量可能会改进 RMPr的目标值,而且负判别数越小,有可能改进 RMPr的目标值越多.相反,具有正判别数的变量无助于改进 RMPr目标值.基于此,本文“差”变量将指具有非负判别数的变量,判别数越大,相应的变量就越差.但需注意,对于任何变量,其判别数会随 RMPr的变化而改变,因此“差”变量在 RMP求解迭代一定次数后,也可能变成非“差”变量,并改进 RMPr的目标值.而且,RMPr对应的变量集与对偶乘子是相互影响的,频繁移除变量可能会影响对偶乘子 πr的稳定性.因此,本文采取每隔一定迭代次数 rout( 列移除频率) 从 RMP 中移除一部分“差”变量,且在列生成的迭代初期和迭代末期,不移除变量.记 zr为的 RMPr目标值, εphase为接近 0的正数.首先,将列生成过程分三个阶段:当 r ＜ 5时,称迭代初期;当 (zr-1-zr)/zr≥ εphase时,为迭代中期;其余为迭代末期.记当前 RMPr的变量数 nr,解中非零基变量的数量为,从 RMPr移除的列数量按如下计算:,此处α ∈ [0,1) 表示从 RMPr中移除“差”变量的比例.

(2)强标号消除准则.

利用 RCSPP 求解子问题时,先构建有向网络图 G(V,A),V 与 A 分别表示节点集和弧集.记 s与 t分别为 G(V,A) 的开始点与结束点.利用多标号动态规划求解 RCSPP 时,用标号表示从 s到达当前节点 i∈ V 的有向路径.这里,ci表示该路径的成本,sri表示该路径消耗资源 r∈ R 的量,R 表示全部资源集.由于每个标号 li都需要通过有向弧 (i,j) 延伸至结点 j( 当满足资源约束时),得到节点 j的标号 lj.因此,标号延伸过程将生成大量标号.为了消除不会成为最优解的标号(只保留 Pareto 最优标号),一般采取如下标号消除准则[11]:

该标号消除方法能够减少各个节点的标号数量,且保证最优标号不会被消除.为了进一步加快求解速度,本文提出一个强标号消除准则,主要是在定义标号消除准则时只考虑部分重要资源集 R⊂ R,从而能消除更多的标号.不失一般性,假定标号消除准则只考虑前个资源,则新的强标号消除准则如下:

此标号消除准则,能够消除更多标号集,但可能会损失某些 Pareto 最优标号.因此,本文在求解子问题时采取二阶段的标号消除准则:在第一阶段使用强消除标号准则;当无法生成具有负判别数的新列时,在第二阶段使用原标号消除准则,从而保证子问题的最优性.需要注意的是,执行强标号消除准则时,如何选取重要资源集 R直接影响二阶段-子问题求解的性能.对于 R的选择,需要根据问题特征或实验方法决定.对于本文所考虑的乘务调度问题,原资源集 R 包含5种资源:a.工作时间长度tw;b.驾驶时间长度 td;c.跨度时间长度 tsp;d.连续驾驶段时长 tspl;e.连续驾驶段数量 nspl.由于工作时间长度 tw直接影响班次成本和效率,本文通过试验也证实该资源是最为重要的资源,对消除大量非最优标号起重要作用.因此,本文利用强标号消除准则时只考虑该资源,即.需要说明的是,强标号消除准则在应用于其他问题如车辆路径问题时,重要资源的选择仍然依赖于问题相关经验或实验方法.

(3)班次池策略加速求解整数解.

利用分支定界求解整数解时,需要在分支树的每个节点调用 RCSPP 求解子问题,从而搜索整个分支定界树将消耗太多时间.本文考虑充分利用父节点已有信息,从而加速子问题求解.方法是:为每个节点设计一个班次池,并继承父节点的班次信息.对于节点 k,包含两个班次集,即班次池与当前 RMP 对应的班次集.若节点 k 的父节点为h,则按如下得到:

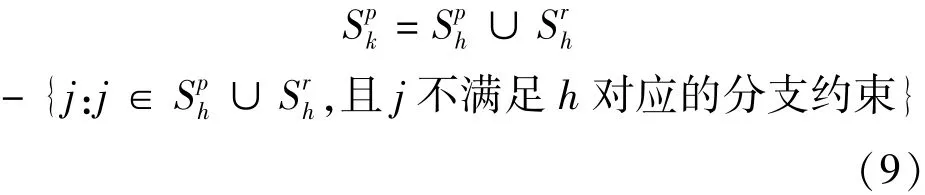
当利用列生成方法求解非根节点 k时,分成两阶段进行:先在班次池 Spk里利用列生成方法,直到无改进当前 RMP 的目标值为止;再利用 RCSPP 调用子问题以得到改进的班次.

3.3 整数解求解

当原问题的线性松弛解是整数解时,则该解即为原乘务调度问题的最优解.否则(分数解),需要利用分支定界方法以求其整数解,本文将利用基于换班机会(RO) 的分支方法.Fores 等[14]曾提出过类似的方法,但没有给出如何选择 RO 的具体方法.记当前分数解对应的班次集 N-,全部换班机会集合 RO.对 ∀r∈ RO,记班次集为

Jr={j|r在班次 j的内部,

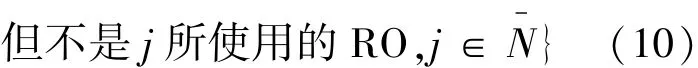
对当前分数解,寻找换班机会 p ∈ RO,使得

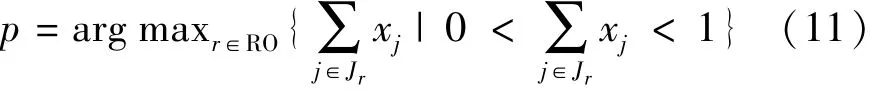
对当前节点采取如下分支:

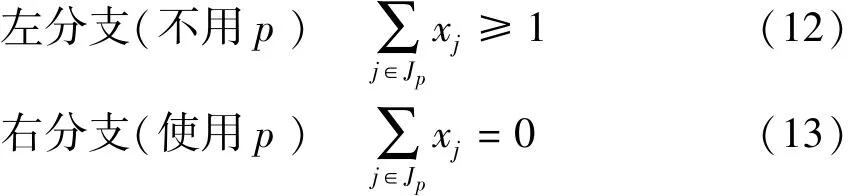
当在整个分支定界树上使用列生成算法时,上述分支策略很容易在子问题中得到实现,只需要删除子问题网络图 G(V,A) 上与分支策略不兼容的弧集即可.

4 计算与实验结果

为测试算法性能,采用实际公共交通中遇到的10 组实例.算法代码用 C++编写,在具有奔腾双核T4300 2.1G 处理器、2 G 内存的笔记本上运行,并利用 CPLEX 12.4 作为线性规划求解器来求解受限主问题 RMP.实验结果中,所有时间用秒表示.

(1)列移除策略与强标号消除规则的实验结果.

在执行列移除策略时,需要设置如下 3个参数:列生成 迭代期划分参数εphase、 移除列频率rout、移除列比例参数 α .先通过一些初步实验,发现列移除频率 rout对算法性能影响很大.因此,先实验确定阶段划分参数 εphase=10-6和移除比例 α = 0.2,再实验 rout的取值.表2 统计了 rout取不同参数值时列生成求解根节点到最优解所需的时间.因为rout太大时,起不到加速作用,只测试了 rout≤ 6 的情况.当 rout=0 时,表示不移除列,此时算法即为传统的列生成方法.表1 的最后一列,记录了利用强标号消除规则后的计算结果.

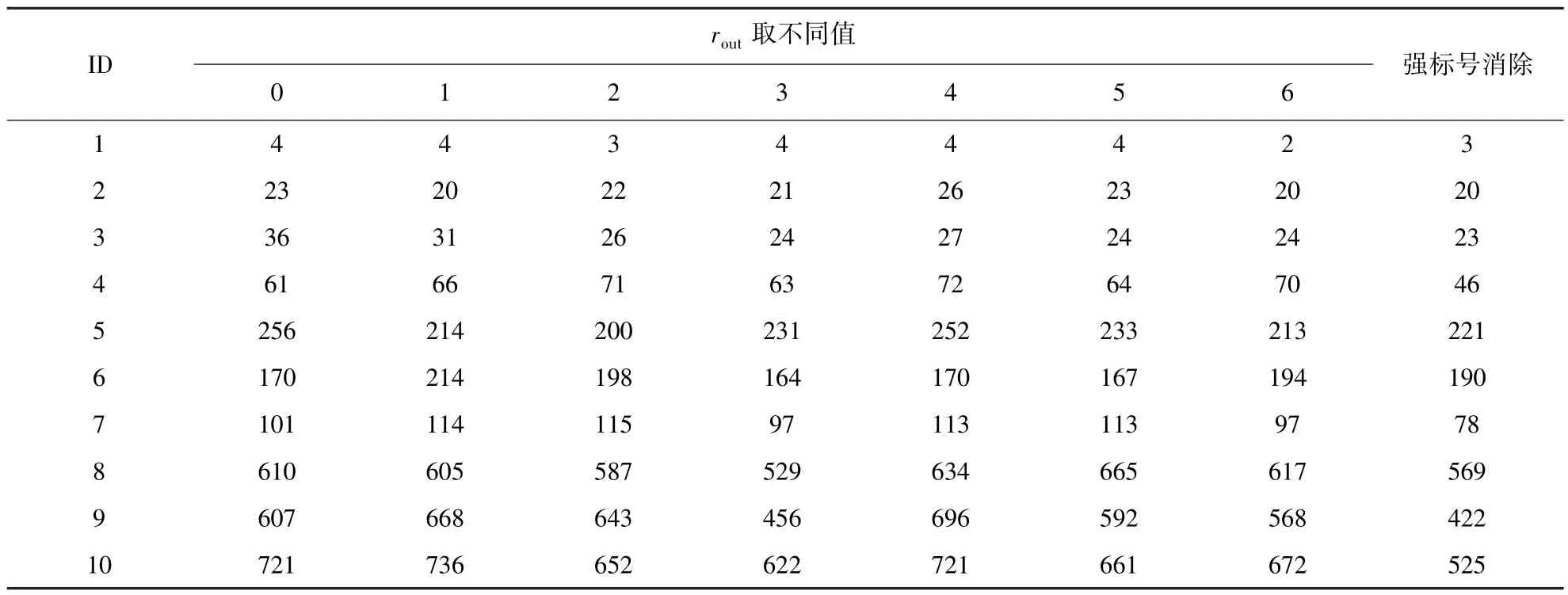
表1 列移除策略与强标号消除规则实验结果Table1 The results of column removing strategy and strong label eliminating rule

从表1 中可以看出,当 rout=3 时采用列移除策略的算法平均性能达到最好( 与 rout=0 比较).从表1的最后一列可以看出,强标号消除准则总体上能进一步降低计算时间.但实例6和实例8的结果差于只采用列移除策略的测试结果.一方面与参数设置有关,另一方面也说明了两种策略同时使用时,其间也会相互影响.

(2)班次池策略实验结果.

测试整数解时,采用深度优先搜索策略,设置最大搜索节点数 nmax=500,分别考虑基于班次池策略的列生成与传统列生成法.表2与表3分别记录了传统列生成法和利用本文班次池策略求解整数解的结果.在表2 与表3 中,“t-RMP”记录求解受限主问题的总时间,“t-SP” 记录求解子问题的总时间,“t-Total” 记录求解整数解的总时间,“ IP”记录最优整数解,“LP-root” 记录根节点线性松弛解,最后一列“nNode”记录求解的节点数,“Gap”计算上下界相对间隙,其计算公式为 Gap=(IP-LP-root)·100/LP-root.

通过比较两种方法,发现本文所提的班次池策略能明显加速列生成方法.10 组实例中,只有第 2组花费了更多时间求解整数解,但其求解的节点数为 500,多于传统列生成方法求解的节点数 155.此外,本文所提的班次池策略,在花费较少求解时间的同时,大多数测试实例都得到了更好(Gap 更小)的整数解.只有第 2 组和第 3 组求得的整数解比传统的列生成方法略差.因此,总体上本文所提的加速策略能够改进传统的列生成方法.

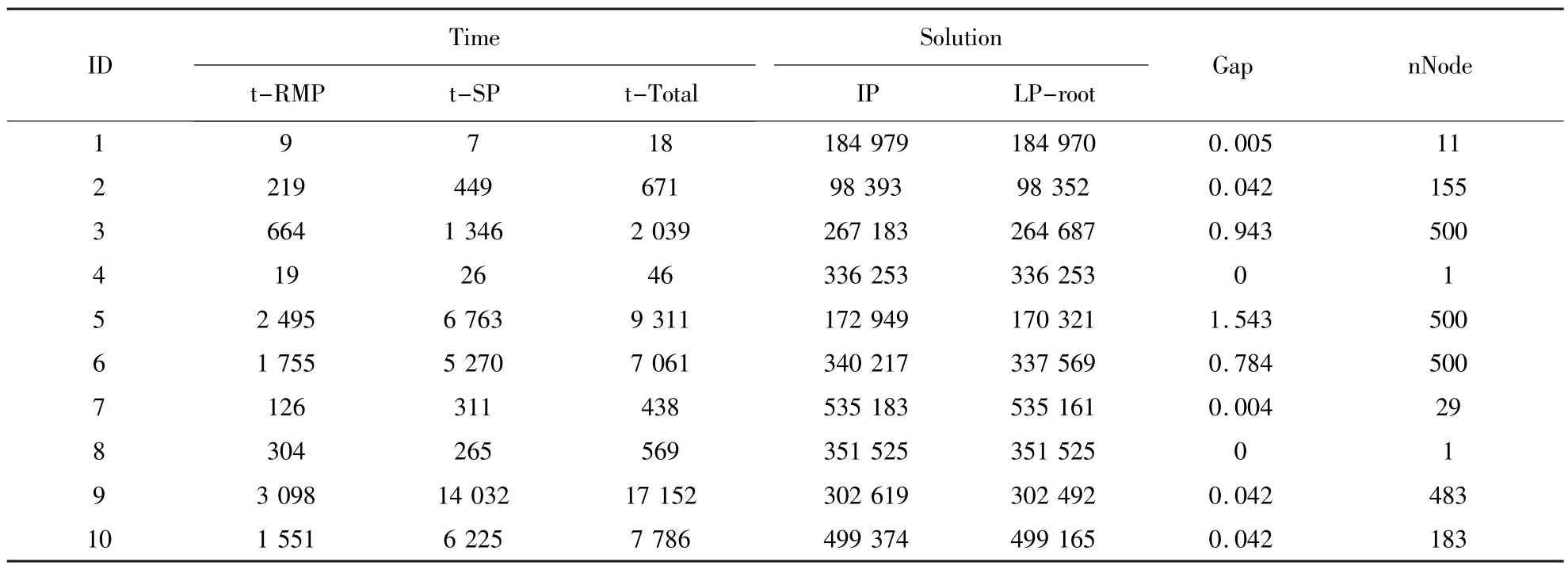
表2 传统列生成方法的整数解Table2 The integer solutions obtained by traditional column generation

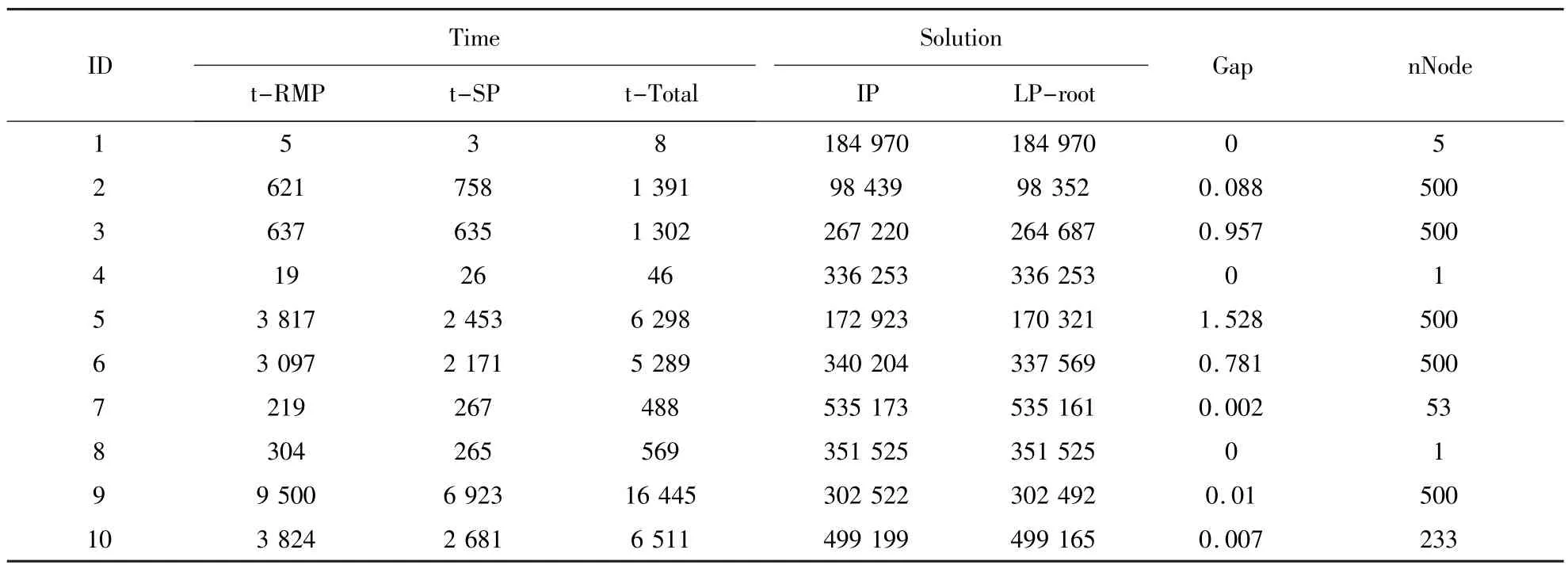
表3 基于班次池策略列生成法的整数解Table3 The integer solutions obtained by the column generation using column pool strategy

5 研究结论

本文基于乘务问题特点,提出了三种加速策略以改进列生成方法,用于求解乘务调度问题.首先,提出了列移除策略,从受限主问题中移除迭代过程中不太可能改进当前目标值的部分列集,目的是减小主问题的求解负担.其次,在求解子问题时,提出一种基于乘务问题特点的强标号消除策略,以减小子问题求解时的标号数量,并提出二阶段子问题求解法.最后,提出利用班次池策略继承已有解的班次信息,加速整数解的求解.通过实际中的 10 组测试实例,表明这些策略能对传统的列生成方法起到改进作用.

[1] Hickman M,Mirchandani P,Voß S(Eds.).Computeraided systems in public transport[M].Lecture notes in economics and mathematical systems,Berlin:Springer, 2008,volume 600.

[2] Lubbecke M E,Desrosiers J.Selected topics in column generation[J].Operations Research,2005,53(6): 1007-1023.

[3] Abbink E,Albino L,Dollevoet T,et al.Solving large scale crew scheduling problems in practice[J]. Public Transport,2011,3(2):149-164.

[4] Gamache M,Soumis F,Marquis G,et al.A column generation approach for large-scale aircrew rostering problems[J].Operations Research,1999,47(2): 247-263.

[5] Gondzio J,González-Brevis P,Munari P.New developments in the primal-dual column generation technique[J]. European JournalofOperational Research,2013,224(1):41-51.

[6] Elhallaoui I,Villeneuve D,Soumis F,et al.Dynamic aggregation of set-partitioning constraints in column generation[J].Operations Research,2005,53(4): 632-45.

[7] Righini G,Salani M.Symmetry helps:bounded bidirectional dynamic programming for the elementary shortest path problem with resource constraints[J]. Discrete Optimization,2006,3(3):255-273.

[8] Righini G,Salani M.New dynamic programming algorithms for the resource constrained elementary shortest path problem[J].Networks,2008,51(3): 155-70.

[9] Leitner M,Raidl G R,Pferschy U.Accelerating column generation for a survivable network design problem[C]//Proceedings of the International Network Optimization Conference,2009.

[10] Alves C,De Carvalho J M V.Accelerating column generation for variable sized bin-packing problems[J]. European Journal of Operational Research,2007,183 2009,26(11):132-135.]

[6] Yi Qi,Lei Yu,Mehdi Azimi,et al.Determination of storage lengths of left-turn lanes at signalized intersections[R]. Journal of the Transportation Research Board,No.2023,Transportation Research Board of the National Academies,Washington,D.C., 2007:102-111.

[7] 李丽丽. 信号交叉口左转交通流中的临界问题研究[D]. 长春:吉林大学,2009:62-63.[LI L L. Research on the critical question of left-turn traffic organization at signalized intersections[D].Chang chun:JiLin University,2009:62-63.] (3):1333-1352.

[11] Feillet D,Dejax P,Gendreau M,et al.An exact algorithm for the elementary shortest path problem with resourceconstraints: Application to some vehicle routing problems[J].Networks,2004,44(3): 216-229.

[12] Chen S,Shen Y.An improved column generation algorithm for crew scheduling problems[J].Journal of Information and Computational Science,2013,10 (1):175-183.

[13] Shen Y,Peng K,Chen K,et al.Evolutionary crew scheduling with adaptive chromosomes [J]. Transportation Research Part B,2013,56(10): 174-185.

[14] Fores S,Proll L,Wren A.TRACS II:a hybrid IP/ heuristic driver scheduling system for public transport [J].Journal of the Operational Research Society, 2002,53(10):1093-100.

Accelerating Column Generation for Solving Crew Scheduling Problems

CHEN Shi-jun,SHEN Yin-dong
(School of Automation,Huazhong University of Science and Technology,Wuhan 430074,China)

Column generation is an efficient math programming approach to solve crew scheduling problems.However,it has the drawback of slow convergence.Three accelerating strategies are presented, based on problem-specific knowledge to speed up its solving process.The first one is to remove some ‘ bad' variables from the restricted master problem after a certain number of iterations.The second one is that a strong label cutting rule is presented,and a two-phase solution approach is proposed to solve the subproblem.The last one is that a shift pool strategy which can use the exiting solution information is proposed to reduce the time to solve integer solutions.Finally,ten real-world instances are tested,and the computational results show that the proposed strategies can accelerate the column generation algorithm.

systems engineering;column generation;accelerating strategies;crew scheduling;problemspecific knowledge

1009-6744(2014)01-0144-06

U268.6

A

2013-09-09

2013-10-31录用日期:2013-11-12

国家自然科学基金(70971044,71171087,61304175).

陈仕军(1980-),男,湖北襄阳人,博士生.*通讯作者:yindong@hust.edu.cn