基于非结构网格的三维中子输运方程求解方法

高 产

(1.中国工程物理研究院 核物理与化学研究所，四川 绵阳 621900；2.中国工程物理研究院 研究生部，北京 100088)

中子输运方程是核反应过程数值模拟的基本方程，是一退化双曲型的积分-微分方程，只在极简单的情况下才能得到解析解，对于一般实际问题，必须采用一些近似方法求解。中子输运方程的数值求解方法[1-3]主要包括离散纵标法、球谐函数法和穿透概率法等。由于求解中子输运方程的离散纵标法实现简单，具有易处理真空边界及计算速度较快的优点，已被广泛应用于核装置以及医学等领域中输运问题的数值求解。离散纵标法对方向变量采用离散纵标离散，对空间变量则采用节块法、有限差分法和有限元法等离散。有限差分法用于较规则的几何问题，不能求解非结构网格问题，三角形节块法虽可求解非结构网格问题，但计算精度不高，而有限元方法可采用任意形状的网格剖分求解区域，对区域的形状有很大的适应性，因此，可应用于非结构网格问题的求解。

随着核能及核技术的发展，反应堆物理计算的发展趋势是精确求解三维任意几何结构的中子输运问题，避免任何均匀化近似。离散纵标-间断有限元方法(DFEM)因可求解任意几何结构的中子输运问题而成为当今研究热点。中子输运方程的有限元求解方法主要有传统的Galerkin法、最小二乘有限元法和间断有限元法。传统的Galerkin法形成的刚度矩阵非对称，不利于方程组的快速迭代求解；最小二乘有限元法未对输运方程做精确处理，难以保证具有较高的计算精度；而间断有限元法在非均匀介质上对输运方程做了精确处理，因而具有较高的计算精度。美国阿拉莫斯国家实验室[4-6]研制了ATTILA程序，基准实验结果表明，ATTILA具有很好的精度和计算速度，并能处理几何复杂的中子输运问题。美国德克萨斯农工大学核能与计算科学系[7]研制了基于非结构网格的并行输运程序PDT，它对输运扫描使用全新的迭代方法，并支持多物理应用。北京应用物理与计算数学研究所研制了二维柱几何Lagrange网格上的非定态中子光子输运程序2DSnDFE，并对它进行了并行化[8-11]。洪振英等[12]将空间线性间断有限元法应用于一维球几何动态粒子输运方程的求解，数值算例表明，空间线性间断有限元法在网格边界的数值精度方面明显高于有限差分法的指数格式和菱形格式，且通量在时间上的微分曲线相对光滑。巨海涛等[13-14]研制了二维和三维非结构网格下求解中子输运方程的程序LESFES，数值计算结果表明，该方法能用于非结构网格，并具有较高的计算精度。

本文研究基于非结构网格的三维中子输运问题的离散纵标-间断有限元计算方法，并开发相应的中子输运计算程序。重点研究每个离散方向的非结构网格的求解顺序的方法以及中子输运DFEM方程中几个矩阵的矩阵元的精确求解方法，并对一系列基准例题进行计算。

1 中子输运方程

考虑区域V、边界δV，各向同性固定源的多群SN方程[5]为：

Sm,g(r)+Qm,g(r)

(1)

(2)

ψm,g(r)=Fm,g(r)n·Ωm<0

(3)

其中：m、g为角度和能群指标；ψ为离散纵标角通量；F为入射角通量；σt为宏观总截面；σs为宏观散射截面；S为用球谐函数Yl,n展开表示的散射源；Q为固定源；n为δV的外方向单位法线矢量；Ω为中子运动方向。

(4)

用线性无关的一组基函数[γp(r),1≤p≤Pk](p为顶点指标；Pk为单元k的顶点数)，定义单元k内的近似角通量和标通量。这些近似函数为：

ψ(r)≅Ψ(r)=ΘT(r)ψ

(5)

φ(r)≅Φ(r)=ΘT(r)φ

(6)

其中：Θ为单元k内的基函数；ψ和φ分别为单元k内的角通量和标通量。

Θ=[γ1(r),…,γPk(r)]T

(7)

ψ=[ψ1,…,ψPk]T

(8)

φ=[φ1,…,φPk]T

(9)

应用Galerkin方法，将式(5)、(6)代入式(4)中，用Θ乘以式(4)，并进行Vk的积分。用高斯散度定理，得到：

(10)

其中：ni为δV的外方向单位法线矢量的第i分量；ψs(r)为单元边界上的角通量。对于每个单元，有：

(11)

其中：l为表面数；Nf为围住单元k的表面总数，如四面体单元的Nf=4，六面体单元的Nf=6。

指定边界的向上侧面的角通量为：

ψs(r)=ΘT(r)ψs,l

(12)

其中，对于第l表面，有：

(13)

其中：ψinc为共用单元k的第l表面的单元的顶点角通量的相应列向量；nav,l为第l表面的平均单位法线矢量，定义为：

(14)

(15)

则每个单元的DFEM方程为：

(16)

其中，

(17)

(18)

(19)

(20)

这些方法的执行仅用到四面体单元的线性基函数。对于四面体网格，对这4个矩阵中的体积积分使用体积坐标，面积积分使用面积坐标，因而这4个矩阵可解析地精确求解，提高计算的速度和精度。

2 中子输运方程的求解方法

对于中子输运方程，递推计算必须沿中子的运动方向进行，这样，在递推过程中边界角通量引进的误差是逐步衰减的，因此，计算格式是稳定的。对于中子输运计算，为加快收敛速度，采用从真空边界向内扫描的方式，本文从第Ⅶ卦限开始计算，计算次序依次是Ⅶ、Ⅷ、Ⅵ、Ⅲ、Ⅴ、Ⅳ、Ⅱ、Ⅰ(表1)。与结构网格求解过程相比，对于某个给定的离散方向Ωm，空间网格的求解顺序不再是按几何位置的顺序依次进行，而是根据Ωm方向通过四面体网格边界的情况决定；空间网格的求解顺序对同一卦限的所有离散方向不再一样，不同的离散方向可能有不同的求解顺序。

对于某离散方向Ωm，在确定空间网格的求解顺序时，需检查每个网格边界的中子流向。对于一个平面，它的外法线矢量方向为n=(a×b)/(|a|·|b|)，据此可得到它的外法线矢量方向的分量nx、ny、nz。通过检验量Ωm·n的符号，就能确定离散方向Ωm通过网格边界的流向。当Ωm·n>0时，这个面是出射面，出射面上的角通量未知；当Ωm·n<0时，这个面是入射面，入射面上的角通量必须已知，否则无法继续求解，通过深度优先搜索和广度优先搜索相结合的方式进行网格求解排序，网格求解排序一次建立并储存起来供以后的扫描使用。

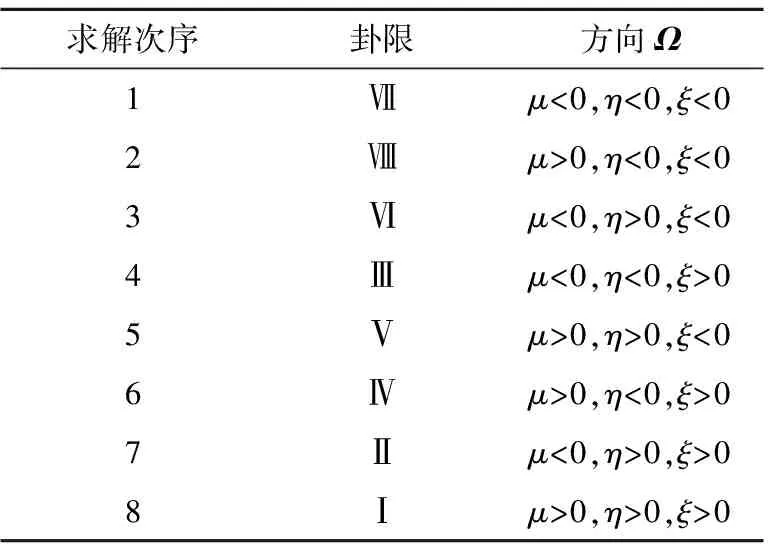
表1 输运扫描次序

3 基准校核

基准问题1[14]是经济合作与发展组织/核能源机构委员会的反应堆物理的一个小压水堆(LWR)的基准问题。考虑两种情况：1) Case1，控制棒位置是空的(真空)；2) Case2，插入控制棒。

基准问题2[14]是经济合作与发展组织/核能源机构委员会的反应堆物理的一个小快增殖堆(FBR)的基准问题。考虑两种情况：1) Case1，控制棒提出(控制棒位置填充Na)；2) Case2，控制棒插进去一半。

基准问题3[15]是为验证应用有限元方法计算非结构网格输运问题所构造的问题，它由一正方形中间套一圆组成。

散方向采用S4求积组；3) 采用的收敛标准为内迭代，Δφ/φ<5×10-4，外迭代，Δkeff/keff<5×10-5。

控制棒价值定义为：

对于基准问题1，计算了两种情况的keff及区域平均中子注量率，SN参考解及开发的TetTran1.0程序的计算结果分别列于表2、3。

表2 基准问题1的keff和控制棒价值

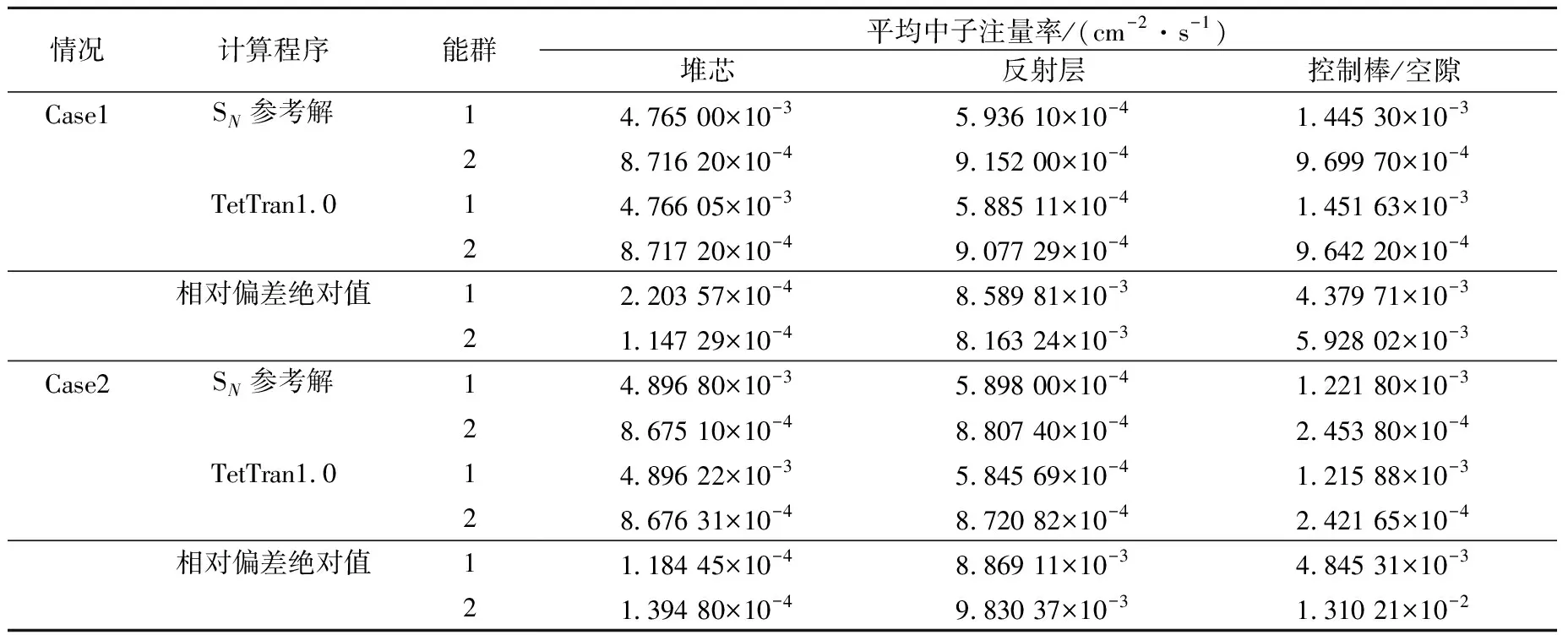
表3 基准问题1的区域平均中子注量率

从表2可看到，TetTran1.0的keff与参考解的相对偏差在0.05%以内，控制棒价值与参考解的相对偏差在0.65%左右。从表3可看到，对于堆芯区域的平均中子注量率，Tet-Tran1.0与参考解的相对偏差在0.022%以内；对于反射层和控制棒/空隙区域的平均中子注量率，TetTran1.0与参考解的相对偏差在1.3%以内。

对于基准问题2，计算了两种情况的keff及区域平均中子注量率，计算结果分别列于表4、5。

表4 基准问题2的keff和控制棒价值

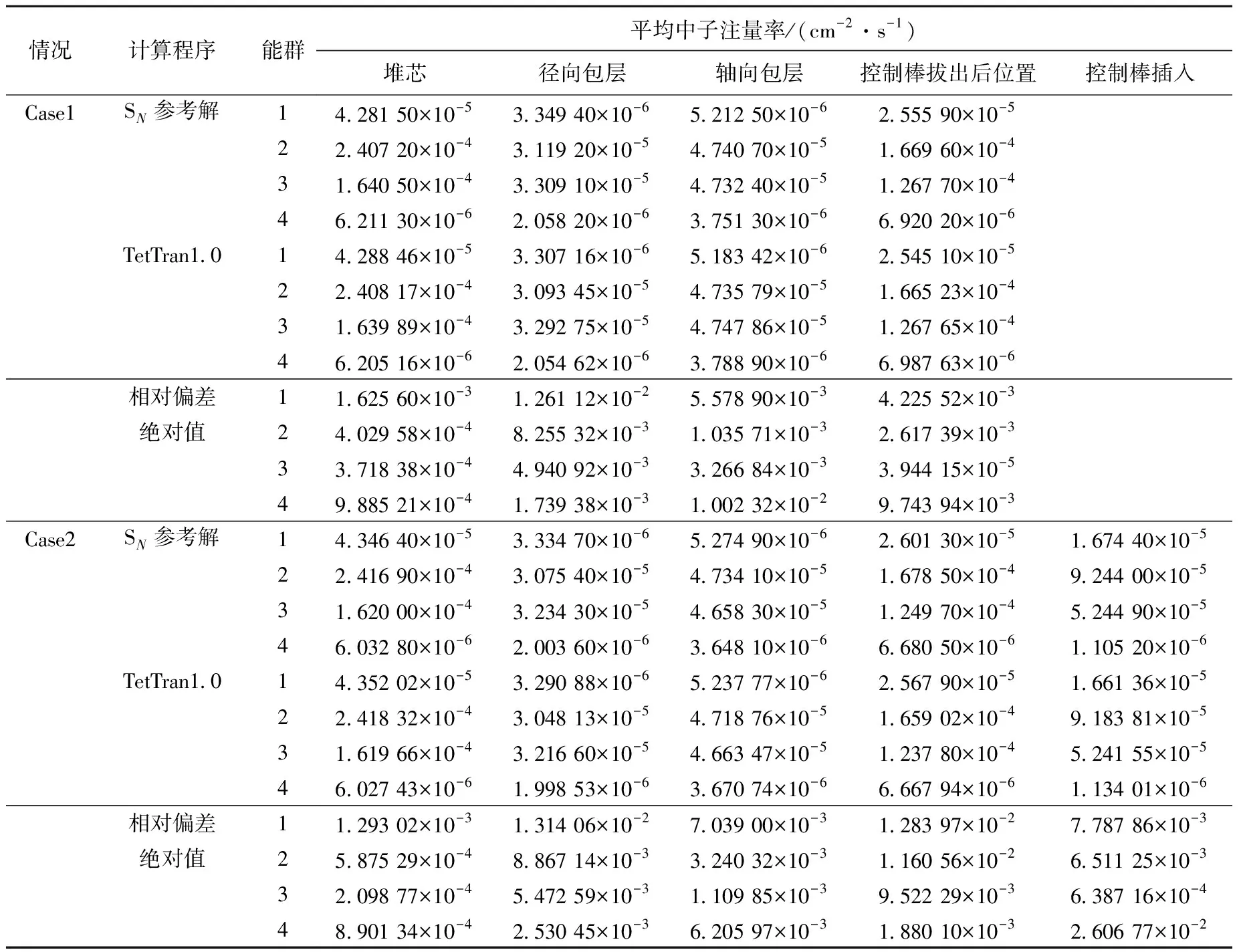
表5 基准问题2的区域平均中子注量率

从表4可看到，TetTran1.0的keff与参考解的相对偏差在0.135%以内，控制棒价值与参考解的相对偏差在2.6%左右。从表5可看到，对于堆芯区域的平均中子注量率，Tet-Tran1.0与参考解的相对偏差在0.16%以内；对于反射层(轴向包层和径向包层)和控制棒区域的平均中子注量率，TetTran1.0与参考解的相对偏差在2.6%以内。

对于基准问题3，计算了keff和每群的区域平均中子注量率，计算结果列于表6、7，其中，以MG-MCNP3B的计算结果作为参考解。

表6 基准问题3的keff

表7 基准问题3的区域平均中子注量率

从表6可看到，TetTran1.0的keff与参考解的相对偏差在0.1%以内，而LESFES的keff与参考解的相对偏差在0.34%。从表7可看到，对于燃料区的平均中子注量率，Tet-Tran1.0与参考解的相对偏差在0.17%以内；对于慢化区的平均中子注量率，TetTran1.0与参考解的相对偏差在1.72%以内。

4 结论

本文使用离散纵标-间断有限元方法求解了三维中子输运方程，它对能量变量采用多群近似离散，对方向变量采用离散纵标法离散，对空间变量采用间断有限元离散；给出了每个SN离散方向的空间网格的求解排序及中子输运DFEM方程中几个矩阵的矩阵元的精确求解方法，并据此开发了基于非结构网格的三维输运计算程序TetTran1.0。基准例题校核表明，该程序具有很高的计算精度。

参考文献：

[1] LEWIS E E, MILLER W F. Computational methods of neutron transport[M]. US: American Nuclear Society, 1993.

[2] 谢仲生，邓力. 中子输运理论数值计算方法[M]. 西安：西北工业大学出版社，2005.

[3] 杜书华，等. 输运问题的计算机模拟[M]. 长沙：湖南科技出版社，1989.

[4] WAREING T A, MCGHEE J M, MOREL J E. ATTILA: A three-dimensional, unstructured tetrahedral mesh discrete ordinates transport code[J]. Trans Am Nucl Soc, 1996, 75: 146-147.

[5] WAREING T A, McGHEE J M, MOREL J E, et al. Discontinuous finite element SNmethods on three-dimensional unstructured grids[J]. Nucl Sci Eng, 2001, 138(3): 256-268.

[6] WARSA J S, WAREING T A, MOREL J E. Fully consistent diffusion synthetic acceleration of linear discontinuous SNtransport discretizations on unstructured tetrahedral meshes[J]. Nucl Sci Eng, 2002, 141(3): 236-251.

[7] ASCI project[M/OL]. http:∥parasol.tamu.edu/asci/web_page.

[8] 阳述林. 高维中子输运方程的离散格式与并行算法研究[D]. 绵阳：中国工程物理研究院，2004.

[9] 莫则尧，傅连祥，阳述林. 非结构网格上求解中子输运方程的并行流水线SN扫描算法[J]. 计算机学报，2004，27(5)：587-595.

MO Zeyao, FU Lianxiang, YANG Shulin. Parallel pipelined SNsweeping algorithm for neutron transport on unstructured grid[J]. Chinese Journal of Computers, 2004, 27(5): 587-595(in Chinese).

[10] MO Zeyao, FU Lianxiang. Parallel flux sweep algorithm for neutron transport on unstructured grid[J]. The Journal of Supercomputing, 2004, 30(1): 5-17.

[11] 魏军侠，阳述林，王双虎，等. 非匹配网格上中子输运方程的间断有限元方法[J]. 核动力工程，2010，31(S2)：25-28.

WEI Junxia, YANG Shulin, WANG Shuanghu, et al. Discontinuous finite element method for neutron transport equations on no matching mesh[J]. Nuclear Power Engineering, 2010, 31(S2): 25-28(in Chinese).

[12] 洪振英，袁光伟. 粒子输运方程的线性间断有限元方法[J]. 计算物理，2009，26(3)：325-334.

HONG Zhenying, YUAN Guangwei. Linear discontinuous finite element method for particle transport equation[J]. Chinese Journal of Computational Physics, 2009, 26(3): 325-334(in Chinese).

[13] 巨海涛，吴宏春，曹良志，等. 二维中子输运方程的非结构网格离散纵标数值解法[J]. 核动力工程，2006，27(3)：1-5.

JU Haitao, WU Hongchun, CAO Liangzhi, et al. Discrete ordinates method for two-dimensional neutron transport equation based on unstructured-meshes[J]. Nuclear Power Engineering, 2006, 27(3): 1-5(in Chinese).

[14] TAKEDA T, IKEDA H. 3D neutron transport benchmarks, technical report OECD/NEA committee on reactor physics (NEACRP-L-330)[R]. Osaka, Japan: Department of Nuclear Engineering, 1991.

[15] CAO Liangzhi, WU Hongchun. Spheriacal harmonics method for neutron transport equation based on unstructured-meshes[J]. Nuclear Sci Tech, 2004, 15(6): 335-339.