熔岩玻璃体239Pu在地下水中的迁移模拟研究
2014-08-07王群书
包 敏,王群书
(西北核技术研究所,陕西 西安 710024)
钚是重要的核武器裂变材料,武器级钚中含有约93.5%的239Pu[1]。239Pu的半衰期约为24 110 a,发射约5 MeV的α粒子,进入人体后主要沉积于肺部和骨骼,生物半排期长,当通过食入和吸入途径摄入体内时会造成严重的内照射,属于极毒性放射性核素,因此它是核环境安全评价的重点关注核素之一。在地下核试验过程中,爆炸释放的能量熔融了装置和部分围岩介质,在冷凝过程中形成熔岩玻璃体,核试验残留的239Pu中约98%包裹在熔岩玻璃体中[1],熔岩玻璃体的溶解速度非常缓慢,因此239Pu在短时间内不会对附近环境产生影响。但239Pu的半衰期很长,熔岩玻璃体缓慢释放出的239Pu会随地下水流动而逐渐发生迁移,有可能污染邻近地区的地下水源。因此需研究熔岩玻璃体内239Pu在地下水中的迁移状况,分析影响其迁移速度的关键因素。
本文针对内华达核试验场帕休特台地一次代号为CHESHIRE的地下核试验,计算239Pu从熔岩玻璃体的溶解释放率,分析239Pu在地下水中的存在形态,采用地下水与溶质运移软件FEFLOW模拟239Pu在地下水中的迁移状况,分析模型中影响239Pu迁移的主要因素。
1 数学模型
CHESHIRE的爆炸威力为200~500 kt,试验后形成半径约80 m的爆炸空腔,产生约3.5×105t的熔岩玻璃体,残留核素239Pu约9.4×1012Bq[2]。熔岩玻璃体密度约为2.5 g/cm3,孔隙度为20%,熔岩玻璃体区域的体积为1.75×105m3。熔岩玻璃体沉积在核试验爆炸空腔的底部,形状近似为球冠,球冠体积V与球冠高度之间的关系式为:
V=πRh2-1/3πh3
(1)
式中:R为球半径,m;h为球冠高度,m,由熔岩玻璃体体积计算得h=28.1 m。模型中采用等体积圆柱体近似描述熔岩玻璃体的形状,圆柱体的半径为44.5 m、高为28.1 m。CHESHIRE爆心处于流纹岩裂隙介质中,位于地下水线之下542 m。近场岩石的渗透性能存在异质性,近似以岩层的平均渗透率建立均质模型。模型采用直角坐标系,以熔岩玻璃体中心为坐标原点,x轴沿地下水流方向,z轴垂直向上,模型空间为-500 m≤x≤1 500 m、-1 000 m≤y≤1 000 m、-100 m≤z≤100 m的饱和含水层,如图1所示。

图1 模型示意图
1.1 熔岩玻璃体溶解模型
熔岩玻璃体在地下水的侵蚀作用下发生溶解反应,释放出239Pu。将熔岩玻璃体简化为大量全等的玻璃体小球,在溶解和放射性衰变两个因素的共同作用下,t时刻239Pu的溶解释放率[3]由式(2)表示:
(2)
式中:G(t)为t时刻239Pu的释放率,Bq/(m3·d);A0为熔岩玻璃体中239Pu的初始活度浓度,Bq/m3,据文献[2],内华达的帕休特台地平均每次地下核试验产生9.40×1012Bq的239Pu,设全部均匀沉积在熔岩玻璃体中,计算得A0为5.37×107Bq/m3;L为熔岩玻璃体的溶解速度,g/(m2·d),L受环境因素影响,与温度、玻璃组分、溶液pH值和饱和度均有关系,文献[2]认为在25 ℃、pH=8.3、与β方石英达到溶解平衡的环境下,流纹岩玻璃的溶解速度为6.693×10-10g/(m2·s),即5.78×10-5g/(m2·d);ρ为熔岩玻璃体小球的密度,ρ=2.5×106g/m3;r0为熔岩玻璃体小球的初始半径,反映了熔岩玻璃体的反应性比表面积,核爆炸产生的挥发性物质在熔岩玻璃体的产生过程中形成气泡,使熔岩玻璃体的反应性比表面积大于高放废物玻璃固化体,文献[2]以0.001 m2/g作为熔岩玻璃体的反应性比表面积,转换为玻璃小球的初始半径为1.2×10-3m;λ为239Pu的衰变常量,λ=7.871 2×10-8d-1。将以上参数代入式(2),计算239Pu释放率,结果示于图2。

图2 熔岩玻璃体239Pu的释放率
从图2可看出,239Pu的最高释放率为3.1 Bq/(m3·d),相当于熔岩玻璃体区域的总释放率为5.43×105Bq/d。CHESHIRE近场岩层的平均地下水渗流速度为0.003 m/d[2],流经熔岩玻璃体的地下水流量约为7.5 m3/d,假设释放出的239Pu完全溶解于地下水,地下水中239Pu的活度浓度将为72.4 Bq/L,约为1.32×10-10mol/L,实验[4]测得Pu(Ⅴ)在内华达地下水中的溶解度约为10-8mol/L,可见熔岩玻璃体溶解释放出的239Pu在地下水中形成化合物的活度浓度远小于239Pu在地下水的溶解度,不会形成239Pu沉淀。
1.2 钚在地下水中的存在形态

(3)
式中:cs为钚的固相活度浓度,Bq/g;c为钚的液相活度浓度,Bq/mL;Kd为分配系数,mL/g。
在内华达地下水中针对粒度为75~500 μm的岩石微粒进行钚的吸附性实验,实验结果表明Kd>500 mL/g[4]。内华达核试验场的地下水中存在大量天然胶体微粒,主要矿物成分是黏土、沸石和方石英。地下水取样监测结果表明,钚离子主要吸附在粒度50 nm~1μm的胶体上[4],这种粒度的胶体较以上吸附实验所使用的固体微粒的粒度更小,因而表面积更大,对钚离子的吸附能力更强,因而Kd会更大。实验研究表明,在内华达地下水环境下,钚离子与胶体结合紧密,在约1 a的实验时间内吸附过程是不可逆的[4]。
CHESHIRE附近地下水中胶体吸附性点位的浓度约为10-9mol/L[5],而吸附于胶体上239Pu的浓度为10-13mol/L[4],可见地下水中胶体吸附性点位的数量远高于239Pu,可近似认为239Pu吸附于胶体是一不可逆的过程,将吸附了239Pu的胶体视为一种可自由迁移的溶质。
本文将熔岩玻璃体溶解释放的239Pu分为两种化学形态:溶解态239Pu和胶体态239Pu,分别对这两种溶质进行迁移模拟计算。溶解态239Pu与岩石介质达到吸附平衡,而胶体态239Pu不受岩石介质的吸附。设熔岩玻璃体释放的239Pu中1%成为胶体态239Pu,其余在地下水与围岩介质之间达到吸附平衡。
1.3 地下水与核素运移模型
将流纹岩裂隙介质简化为等效孔隙介质,饱和含水层中地下水运动方程为:
(4)
式中:H为地下水的水头,m;K为饱和含水层的渗透系数,m/d;S0为饱和含水层的贮水率,m-1。方程中H为待求解的物理量,K和S0为模型参数。
现场抽水试验测定CHESHIRE近场饱和含水层的平均渗透系数为0.30 m/d[2];模型中将岩石介质简化为各向同性的均匀介质,K取0.30 m/d。
S0表示水头下降1个单位使单位体积饱和含水层释放出的水体积,采用下式[6]计算:
S0=ρg(α+nβ)
(5)
式中:ρ为地下水密度,1 000 kg·m-3;g为重力加速度,9.8 m·s-2;α为岩层的压缩系数,裂隙岩层的压缩系数取值范围为10-11~10-9Pa-1 [7];n为岩石介质的孔隙度,CHESHIRE附近的有效孔隙度近似为0.01[2];β为地下水的压缩系数,取值4.4×10-10Pa-1。取α为10-10Pa-1,计算得S0为1×10-6m-1。由式(4)求得H后,利用Darcy定律计算饱和含水层的地下水孔隙流速:
(6)
式中:v为地下水孔隙流速,m/d;n为饱和含水层的有效孔隙度,无量纲。取流纹岩裂隙介质的有效孔隙度为0.01,熔岩玻璃体区域的有效孔隙度为0.2[2]。
在连续介质中,239Pu的运移方程为:
(7)
式中:c为239Pu的液相活度浓度,Bq/m3;ρb为含水层固相介质的密度,取2.7 g/cm3;Kd为239Pu的分配系数,是吸附于岩石介质的239Pu活度浓度与水中239Pu活度浓度的比值,反映了岩石介质对239Pu的吸附能力,溶解态239Pu的分配系数选用文献[3,7]中给出的值500 mL/g,胶体态239Pu的分配系数取零;Q为239Pu源汇项,在熔岩玻璃体区是239Pu的溶解释放率(图2),在模型其他区域为零;D为弥散系数,可分解为沿地下水流方向的纵向弥散系数DL和垂直地下水流方向的横向弥散系数DT,计算公式为:
DL=αL|v|+D*
(8)
DT=αT|v|+D*
(9)
其中:αL为纵向弥散度,m;αT为横向弥散度,m;D*为核素在地下水中的有效分子扩散系数,取1×10-9m2/s;|v|为地下水孔隙流速,m/s。αL和αT受观测尺度影响,随观测尺度的增大而增大,根据59个野外场地纵向弥散度与观测尺度之间的关系[8],当观测尺度约为1 000 m时,αL取10~100 m,横向弥散度约较纵向弥散度小一个数量级。本文取50 m和5 m作为αL和αT的参数。方程(7)中c为待求解的未知量,其余各量是模型参数。
式(4)和式(7)分别为求解未知量H和c的偏微分方程,它们反映了饱和含水层内地下水与溶质的运动关系,物质运动还与初始条件和边界条件有关,偏微分方程和初始、边界条件一起构成模型空间内的定解数学问题。
模型x=-500 m和x=1 500 m边界面与地下水流垂直,视为等水头边界,其中x=-500 m边界面是新鲜地下水的入流边界,设置为零活度浓度边界,x=1 500 m边界面是地下水的出流边界,设为零活度浓度梯度边界;CHESHIRE近场地下水的水力梯度为0.005~0.015[2],模型中取0.01,以上两边界面之间的水头差为20 m。边界平面y=-1 000 m、y=1 000 m、z=-100 m和z=100 m设置为隔水边界。
2 FEFLOW建模
采用FEFLOW软件对以上239Pu迁移模型进行数值计算。FEFLOW是丹麦DHI-WASY公司的专业地下水与溶质迁移数值计算软件,采用有限元方法进行数值计算,软件功能包括模型空间网格剖分、可视化参数输入、有限元数值计算和模拟结果的可视化输出。
对模型空间进行三维网格剖分。采用三角形网格在水平面上进行二维空间剖分,在熔岩玻璃体区域附近核素的活度浓度变化量大,网格剖分细密,网格尺度约为10 m;其余区域核素活度浓度变化量小,网格剖分粗,尺度约为50 m。共剖分为5 831个三角形网格,如图3所示。

图3 二维有限元网格设计
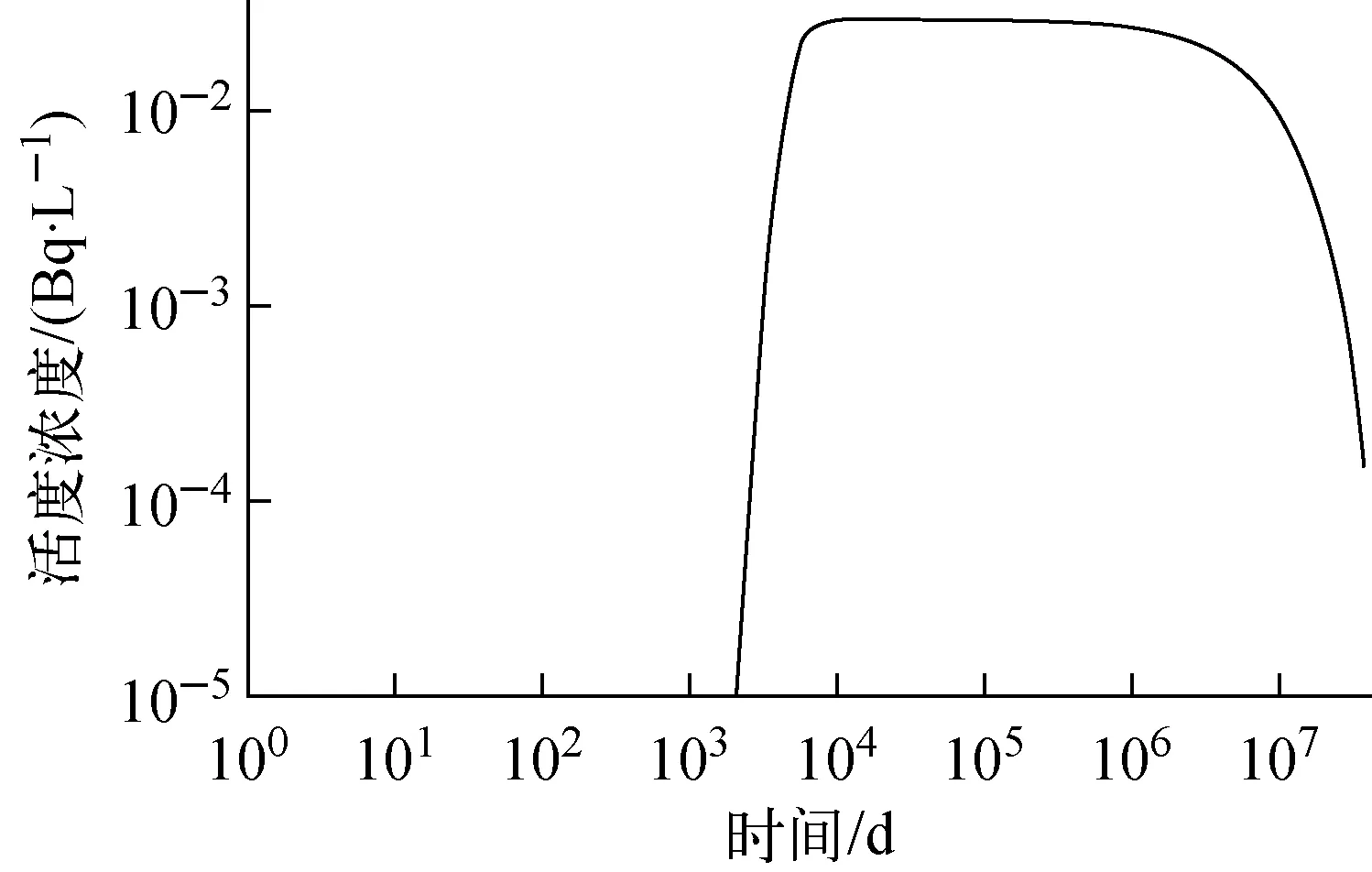
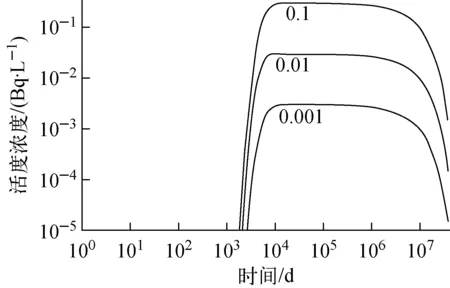
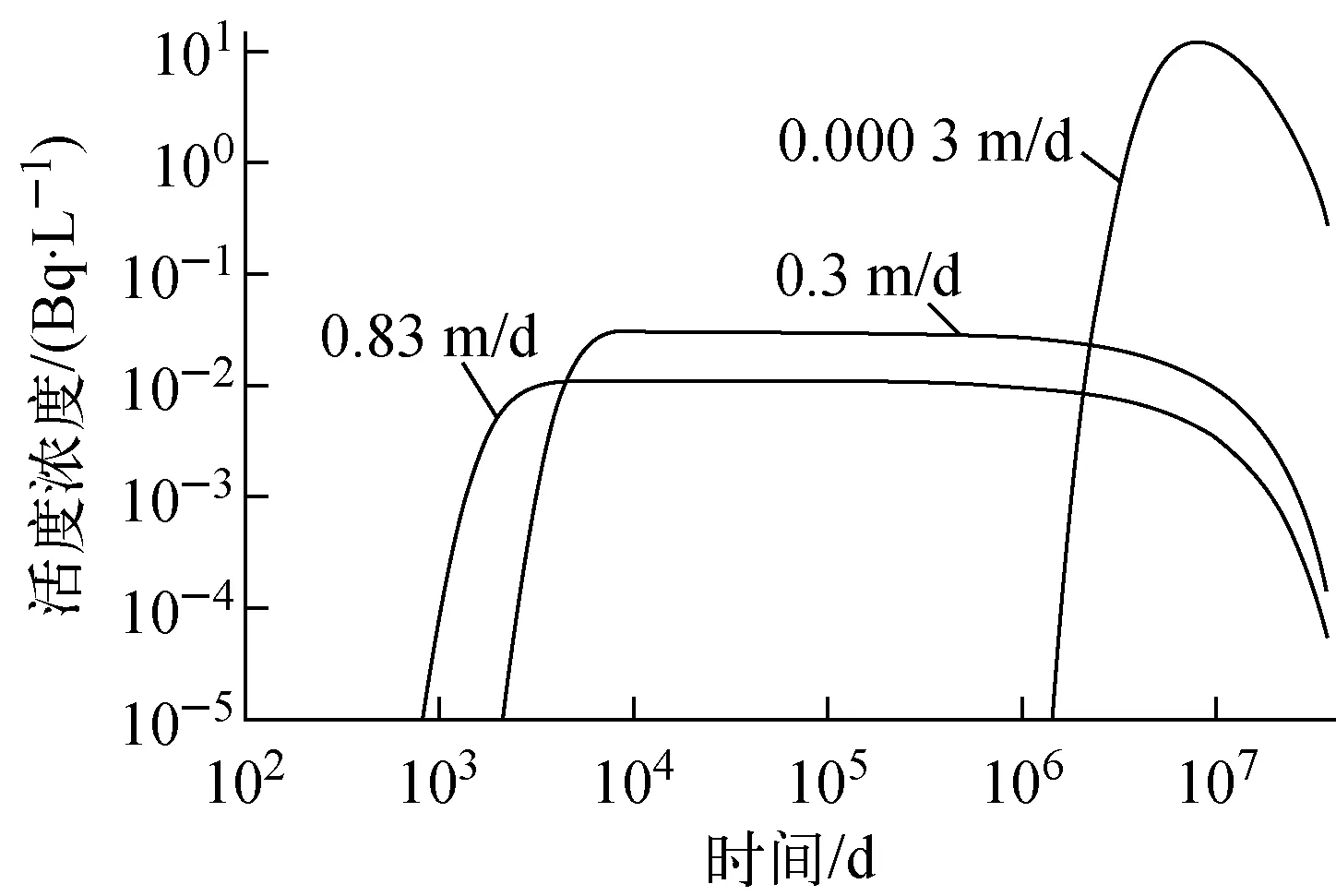
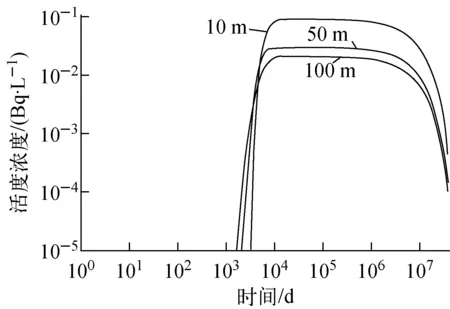
将二维网格扩展到三维,其中-20 m≤z≤20 m区域包含有熔岩玻璃体,由于核素活度浓度变化大,因此垂向空间剖分较密,剖分了-20、-14.1、-14、-10、-5、0、5、10、14、14.1、20 m共11个剖面,熔岩玻璃体设置在剖面-14 m到14 m之间。在-100 m≤z<-20 m和20 m 图4 三维有限元网格 分别以溶解态239Pu和胶体态239Pu为溶质,建立239Pu在CHESHIRE近场的迁移模型,运用FEFLOW可视化参数输入模块输入地下水与核素运移的模型参数,模拟239Pu污染羽的发展状况。将模型运行10万年,239Pu共经历4.15个半衰期,核素总量衰减为初始值的5.64%。在熔岩玻璃体中心剖面(z=0 m平面)上,沿着过爆心的地下水的流线,在距爆心1.3 km处设置观测点(图3),记录观测点位置的239Pu活度浓度在不同时刻的模拟值。 在10万年的模拟时间内,观测点的溶解态239Pu的模拟活度浓度始终小于10-15Bq/L,说明没有溶解态239Pu能够迁移到这里。图5为在熔岩玻璃体中心平面(z=0 m平面)上1万年和10万年的溶解态239Pu的污染羽模拟结果。由图5可见,溶解态239Pu的扩散迁移速度非常缓慢,10万年内沿地下水流向扩散迁移的距离不大于300 m。 模拟时间:a——1万年;b——10万年 在10万年的模拟时间内,观测点胶体态239Pu的模拟活度浓度示于图6。由图6可见,约2 000 d后胶体态239Pu到达观测点,在4 000~1×107d(即11~27 000 a)内观测点胶体态239Pu的活度浓度维持在约0.01 Bq/L,说明胶体态239Pu将以相同的活度浓度水平长期存在于核试验爆心下游的地下水中。在1×107d后,胶体态239Pu活度浓度逐渐减弱,这主要是由熔岩玻璃体释放239Pu的量逐渐减少所致。 在熔岩玻璃体中心平面(z=0 m平面)上,胶体态239Pu在2 000、10 000、1×106和3.65×107d的污染羽分布示于图7。由图7可见,胶体态239Pu的污染羽沿地下水流向下游延伸,活度浓度逐渐减弱。10 000 d 和1×106d的胶体态239Pu污染羽的活度浓度分布基本一致,爆心附近的239Pu活度浓度处在同一量级水平。 图6 观测点的胶体态239Pu活度浓度模拟结果 模拟时间:a——2 000 d;b——10 000 d;c——1×106 d;d——3.65×107 d 比较溶解态239Pu和胶体态239Pu的迁移模拟结果可知,溶解态239Pu不可能发生远距离迁移,而胶体态239Pu将在爆心下游形成长期恒定的239Pu活度浓度。从CHESHIRE试验点向西约5 km、向南约1 km是内华达帕休特台地的另一次地下核试验BENHAM的试验点,在BENHAM试验之后约30 a(即10 958 d),在其爆心的地下水下游1.3 km处测量到239Pu的活度浓度在10-2~10-4Bq/L之间,且99%以上的239Pu以胶体态存在[4]。该观测结果与模型中胶体态239Pu的模拟结果相符,这也间接证明模型所采用的假设是合理的。 模型中影响239Pu迁移的参数包括胶体态239Pu所占份额、熔岩玻璃体的溶解速度、分配系数、岩层的渗透系数、有效孔隙度和弥散度。以观测点239Pu活度浓度作为目标模拟量,在固定其他参数不变的前提下1次改变1个参数的取值,分析参数值变化对目标模拟量的影响程度,进而判断模型参数的重要程度。 熔岩玻璃体溶解释放出239Pu,在地下水环境下可能与天然胶体微粒结合形成胶体粒子,也可能以溶解态存在。239Pu形成胶体粒子的比例与特定场址的地下水环境有关,本文分别取胶体态239Pu占熔岩玻璃体释放量的0.001、0.01、0.1计算观测点239Pu的活度浓度,结果示于图8。由图8可见,观测点胶体态239Pu的活度浓度与熔岩玻璃体溶解产生239Pu胶体的份额呈正比,份额增加10倍,观测点胶体态239Pu活度浓度增大10倍;反之份额减少10倍,观测点胶体态239Pu活度浓度也减少10倍。 图8 胶体态239Pu份额对观测点胶体态239Pu活度浓度的影响 熔岩玻璃体溶解速度受环境因素影响,在中性、密闭的平衡系统中,玻璃体溶解速度缓慢,流纹岩玻璃体在25 ℃的溶解速度下限为2.4×10-12g/(m2·s)[2],即2.07×10-7g/(m2·d)。在酸性或碱性环境中熔岩玻璃体溶解速度加快,流纹岩玻璃在25 ℃、pH=12的碱性环境中溶解速度上限为4.4×10-8g/(m2·s)[2],即3.80×10-3g/(m2·d)。本文分别以熔岩玻璃体的溶解速度2.07×10-7、5.78×10-5、3.80×10-3g/(m2·d)计算239Pu释放率,模拟溶解态239Pu和胶体态239Pu迁移状况。模拟结果表明,溶解速度对溶解态239Pu的目标模拟量无影响,溶解态239Pu始终无法迁移到观测点;胶体态239Pu受玻璃体溶解速度的影响较大,各溶解速度条件下观测点的胶体态239Pu活度浓度模拟结果示于图9。由图9可见,高溶解速度下胶体态239Pu达到观测点的时间早、活度浓度高,这是由于模型中熔岩玻璃体释放出的胶体态239Pu的量多引起的。后期由于高溶解速度对应的熔岩玻璃体239Pu释放率减少,观测点239Pu活度浓度也随之降低。 图9 熔岩玻璃体溶解速度对观测点胶体态239Pu活度浓度的影响 CHESHIRE近场岩层的渗透性可划分为高、中、低和极低岩层,对应渗透系数分别为0.83、0.016、0.003 1、0.000 3 m/d[2],其中高渗透岩层占37%,中渗透岩层占46%,低渗透和极低渗透岩层共占17%,平均渗透系数为0.3 m/d。分别将模型岩层的渗透系数设置为0.83 m/d和0.000 3 m/d,计算渗透系数对溶解态239Pu和胶体态239Pu迁移的影响。模拟结果表明,溶解态239Pu在岩层渗透系数设置为0.83 m/d时依然无法迁移到观测点,说明即使爆心处在高渗透岩层,溶解态239Pu依然无法发生远距离迁移。胶体态239Pu在不同岩层渗透系数下的模拟结果示于图10。由图10可见,当岩层渗透系数高时,地下水渗流速度快,胶体态239Pu迁移到观测点需要的时间短,但由于流经熔岩玻璃体的水流量大,对胶体态239Pu产生稀释作用,降低了地下水中胶体态239Pu的活度浓度。而当岩层渗透系数较低时,地下水渗流速度慢,胶体态239Pu到达观测点需要较长时间,由于流经熔岩玻璃体的地下水流量少,地下水中胶体态239Pu的活度浓度偏高。 图10 渗透系数对观测点胶体态239Pu活度浓度的影响 地下水中胶体态239Pu不受岩石介质的吸附,分配系数取0 mL/g。溶解态239Pu受岩石介质的吸附,影响吸附作用的因素很多,包括核素在地下水中的化学形态、地下水组分、岩石矿物成分等。静态批式法测量钚在尤卡山凝灰岩介质上的分配系数介于10~1 000 mL/g之间[2]。本文分别以10 mL/g和100 mL/g作为溶解态239Pu分配系数的可选值,分析分配系数对溶解态239Pu迁移的影响程度。计算结果示于图11。由图11可见,分配系数影响观测点溶解态239Pu的到达时间和活度浓度峰值,当分配系数取100 mL/g时,在10万年内观测点溶解态239Pu模拟活度浓度始终小于10-6Bq/L;当分配系数取10 mL/g时,观测点溶解态239Pu活度浓度在1.5×107d时达到峰值0.1 Bq/L。可见,岩石介质对239Pu的吸附作用能强烈阻滞溶解态239Pu发生迁移,当溶解态239Pu的分配系数大于10 mL/g后将不可能发生公里距离以上的迁移。 图11 分配系数对溶解态239Pu迁移的影响 有效孔隙度反映了岩层内连通导水的孔隙占岩石总体积的比例。CHESHIRE近场示踪试验测得的有效孔隙度为0.008~0.023[2]。本文取有效孔隙度为0.008、0.023和0.01,计算溶解态239Pu和胶体态239Pu在观测点的活度浓度。计算结果表明,无论有效孔隙度取何值,溶解态239Pu均无法迁移到观测点。胶体态239Pu在观测点的活度浓度模拟结果示于图12。由图12可见,有效孔隙度越大,胶体态239Pu达到观测点的时间越晚。这是因为在地下水渗流速度固定的前提下,有效孔隙度增大导致孔隙地下水流速变慢,使得胶体态239Pu的迁移速度变慢,但流经熔岩玻璃体的地下水流量未发生变化,所以观测点胶体态239Pu活度浓度不受影响。 当观测尺度约为1 000 m时,纵向弥散度的取值介于10~100 m之间[8]。分别取纵向弥散度为10、50和100 m,横向弥散度取对应纵向弥散度的10%,计算溶解态239Pu和胶体态239Pu在观测点的活度浓度。模拟结果表明,无论弥散度取何值,溶解态239Pu均无法迁移到观测点位置。胶体态239Pu活度浓度模拟结果示于图13。由图13可见,弥散度越大,胶体态239Pu到达观测点的时间越早。高弥散度条件下胶体态239Pu的扩散空间大,导致弥散度高时观测点239Pu活度浓度低于弥散度低时的情况。 图12 有效孔隙度对观测点胶体态239Pu活度浓度的影响 图13 弥散度对观测点胶体态239Pu活度浓度的影响 对CHESHIRE近场环境条件下溶解态239Pu和胶体态239Pu的迁移模拟结果表明:溶解态239Pu受岩石介质强烈吸附,不能发生远距离迁移,影响溶解态239Pu迁移的关键模型参数是分配系数,当分配系数大于10 mL/g后即可忽略溶解态239Pu的远距离迁移。胶体态239Pu不受岩石介质吸附,在爆心下游形成相对固定的污染晕,污染晕内的胶体态239Pu活度浓度长时间维持在相同水平,在距爆心1.3 km处的观测点胶体态239Pu活度浓度的模拟结果为10-2Bq/L,与内华达核试验场BENHAM近场观测孔的监测数据相符。模型中影响胶体态239Pu迁移的主要因素包括熔岩玻璃体的溶解速度、熔岩玻璃体溶解产生239Pu胶体的比例和岩层的渗透系数。熔岩玻璃体的溶解速度和形成胶体比例决定了爆心释放胶体态239Pu的数量,岩层的渗透系数决定了地下水的渗流速度。模拟结果表明,只有当239Pu形成胶体粒子后才可能发生远距离迁移,这与内华达核试验场的监测数据[4-5]是一致的。 参考文献: [1] IAEA. The radiological situation at the atolls of mururoa and fangataufa volume 3: Inventory of radionuclides underground at the atolls, IAEA-MFTR-3[R]. Vienna: IAEA, 1998. [2] PAWLOSKI G A, TOMPSON A F B, CARLE S F, et al. Evaluation of the hydrologic source term from underground nuclear tests on Pahute Mesa at the Nevada Test Site: The CHESHIRE test[R]. Livermore: Lawrence Livermore National Laboratory, 2001. [3] IAEA. The radiological situation at the atolls of mururoa and fangataufa volume 4: Releases to the biosphere of radionuclides from underground nuclear weapon tests at the atolls, IAEA-MFTR-4[R]. Vienna: IAEA, 1998. [4] KERSTING A B, EFURD D W, FINNEGAN D L, et al. Migration of plutonium in ground water at the Nevada Test Site[J]. Nature, 1999, 397: 56-59. [5] ANDREW W, LEE G, LU G P, et al. TYBO/BENHAM:Model analysis of groundater flow and radionuclide migration from underground nuclear tests in Southwestern Pahute Mesa, Navada, LA-13977[R]. US: Los Alamos National Laboratory, 2002. [6] 吴吉春,薛禹群. 地下水动力学[M]. 北京:中国水利水电出版社,2009:28-33. [7] DUFFIELD G M. Representative values of hydraulic properties[EB/OL]. (2010)[2012-04-20]. http:∥ www.aqtesolv.com/aquifer_tests/aquifer_properties.htm. [8] 郑春苗,BENNETT G D. 地下水污染物迁移模拟[M]. 2版. 北京:高等教育出版社,2009:199.
3 模拟结果
3.1 溶解态239Pu模拟结果

3.2 胶体态239Pu模拟结果

4 参数敏感度分析
4.1 胶体态239Pu份额
4.2 熔岩玻璃体溶解速度

4.3 渗透系数
4.4 分配系数

4.5 有效孔隙度
4.6 弥散度

5 结论
